大学应用数学-方差性质简介

1.方差的概念

数学期望是随机变量的一个重要数字特征，它描述了随机变量取值的平均状况.但在很多情况下，只知道随机变量的数学期望是不够的，还需要知道它们所取的值与平均值的偏离程度.例如，用机器包装袋装牛奶，我们不仅要知道各袋重量X的平均值E（X）的大小，还要知道各袋质量距平均值E（X）的偏离程度.在平均重量合格的情况下，偏离程度越小，表明机器工作越稳定，否则可以认为机器工作不够正常.

如何来衡量随机变量的偏离程度呢?人们自然想到用偏差——[X-E（X）]的平均值，但由于偏差有正有负，有可能出现正负偏差相互抵消的情形，而用的平均值，则会产生数学处理上的诸多不便，故采用指标E[X-E（X）]2——偏差平方的平均值——方差来描述随机变量的偏离程度.

设X是一个随机变量，若E[X-E（X）]2存在，则称它为随机变量X的方差，记作D（X）.而称为随机变量X的均方差（或标准差），即

D（X）=E[X-E（X）]2

由方差的定义可知，计算方差的实质是求随机变量[X-E（X）]2的数学期望，因此有下列方差的具体计算公式：

（1）如果X是离散型随机变量，且P（X=xi）=pi，i=1，2，…，则

（2）如果X是连续型随机变量，且有概率密度f（x），则

（3）常用的方差计算公式：

D（X）=E（X2）-[E（X）]2

事实上，利用方差的定义及数学期望的性质有

例8.33　设X～0-1分布，求D（X）.

解　由题意知，X的分布列为：P（X=1）=p，P（X=0）=1-p=q（0＜p＜1）.因为E（X）=p，E（X2）=12·p+02·q=p，所以有

D（X）=E（X2）-[E（X）]2=p-p2=p（1-p）=pq

同理，当X～P（λ）时，D（X）=λ.

另外根据下面方差的性质等可求得：当X～B（n，p）时，D（X）=npq.

例8.34　设X～U[a，b]，求D（X）.

解　由X～U[a，b]，得，而，于是

同理：（1）当X～e（λ）时，D（X）=；（2）当X～N（μ，σ2）时，D（X）=σ2.

由此可见，正态分布中的参数μ，σ2分别是随机变量的数学期望和方差，因此若均值和方差已知，则可以完全确定正态分布的概率密度函数及其分布函数.

2.方差的性质(www.xing528.com)

设D（X）存在，则有下列性质：

（1）D（C）=0（C为常数）.

（2）D（aX）=a2D（X）（a为常数）.

推论8.4　D（-X）=D（X）.

（3）D（X+b）=D（X）.

（4）D（X±Y）=D（X）+D（Y）±2E{[X-E（X）][Y-E（Y）]}.

特别地，当X，Y相互独立时，有

D（X±Y）=D（X）+D（Y）

推论8.5　若X1，X2，…，Xn相互独立，则

D（X1+X2+…+Xn）=D（X1）+D（X2）+…+D（Xn）

例8.35　设随机变量X1，X2，…，Xn相互独立，且均服从N（μ，σ2）分布，求随机变量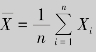的数学期望和方差.

例8.36　若X～N（μ，σ2），且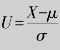，试证明E（U）=0，D（U）=1.

练习8.3

1.对某一目标进行射击，直到击中目标为止，若每次射击命中率为p，求射击次数的期望与方差.

2.设离散型随机变量X服从参数为2的泊松分布，求随机变量Z=3X-2的期望与方差.

3.已知随机变量X服从二项分布，且E（X）=2.4，D（X）=1.44，求二项分布的参数n，p的值.

4.设随机变量的分布列为

求E（X）和D（X）.

5.设随机变量X具有密度函数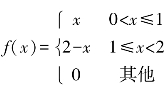，求E（X），D（X）.