连续型随机变量的概率分布-来自《大学应用数学》

1.连续型随机变量及其概率密度

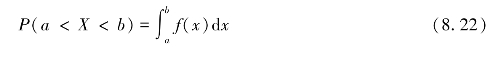
对于随机变量X，若在实数集R上存在非负可积函数f（x），对任意实数a，b（a＜b）都有则称X为连续型随机变量.称f（x）为连续型随机变量X的概率密度函数，简称概率密度或密度函数.

概率密度f（x）具有下列两个基本性质：

（1）非负性：f（x）≥0.

可以证明：满足上述两个基本性质的函数f（x）可作为某一连续型随机变量的概率密度.

对于连续型随机变量X，因为，所以

P（X=c）=0

可见，概率为0的事件不一定是不可能事件，概率为1的事件也不一定是必然事件.

由此可知，在计算连续型随机变量落在某一区间内的概率时，区间是否包含端点是无须考虑的，即

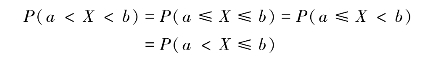
2.连续型随机变量的分布函数

若连续型随机变量X的概率密度为f（x），则随机变量X的分布函数为：

由微积分的知识可得：

（1）连续型随机变量的分布函数F（x）处处连续.

（2）在密度函数f（x）的连续点处，有

式（8.24）与式（8.25）表明了连续型随机变量X的概率密度与分布函数之间的关系，它们之中已知一个可求得另一个，这是非常自然的，因为二者都是刻画随机变量X概率分布的工具.

例8.24　设连续型随机变量X的概率密度为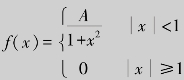，求：（1）系数A；（2）分布函数F（x）；（3）P（0＜X≤）.

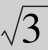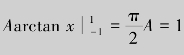解　（1）由式（8.23），得，即，解得

（2）由式（8.24），得，因为f（x）为分段函数，所以当x≤-1时，

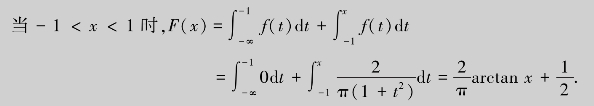
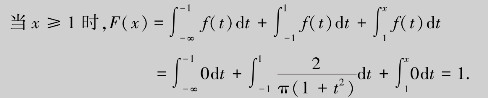
于是分布函数为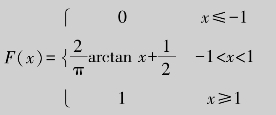

（3）由式（8.26），得

例8.25　设连续型随机变量X的分布函数为

F（x）=a+barctan x（-∞＜x＜+∞）

（1）确定常数a，b；（2）求随机变量X的概率密度函数；（3）求P（-1≤X≤1，P（X2＞1）.

解　（1）根据分布函数的性质，有

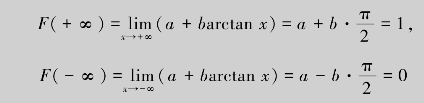
联立上面两式解得：

（2）由（1）知，，由密度函数f（x）=F′（x），得

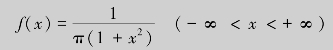
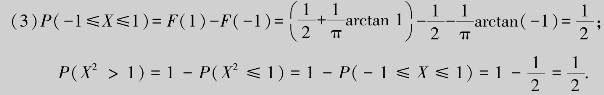
3.几种常见的分布

（1）指数分布.若连续型随机变量X的概率密度为

其中λ＞0，则称随机变量X服从参数为λ的指数分布，记作：X～e（λ）.

可以求得，服从指数分布的随机变量X的分布函数为：

指数分布常作为各种“寿命”分布的近似，如电子元件、电路中的保险丝、轴承、宝石等的使用寿命、服务时间等.

例8.26　设某电子元件的寿命X（年）服从参数为3的指数分布，（1）求该电子元件寿命超过2年的概率；（2）已知该电子元件已使用了1.5年，求它还能使用2年的概率.

解　电子元件的寿命X的概率密度为

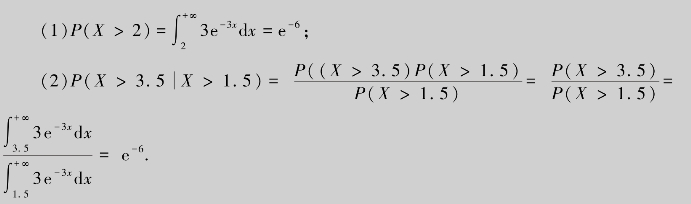
（2）均匀分布.若连续型随机变量X在有限区间[a，b]内取值，且其概率密度为

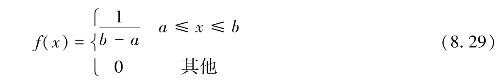
则称随机变量X在[a，b]上服从均匀分布（图8.9），记作：X～U[a，b].

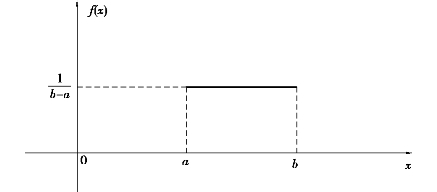
图8.9

直观地讲，均匀分布反映了X在[a，b]上各点取值是等可能的，故冠以“均匀”.严格地说，X落在[a，b]中任一子区间上的概率与该子区间长度成正比，而与子区间的位置无关.事实上，对于任意的，此值与c无关.

可以计算，服从均匀分布的随机变量X的分布函数为：

F（x）的图形如图8.10所示，它是一条连续曲线.

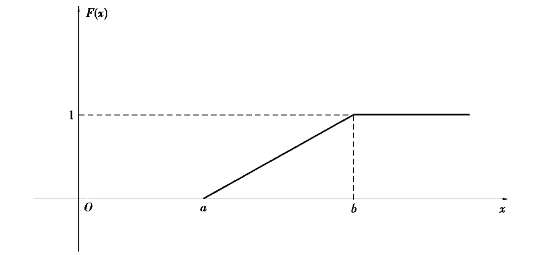
图8.10

实际问题中，服从均匀分布的例子很多，如计算机的舍入误差服从[-0.5，0.5]上的均匀分布；任一时刻来到汽车站，等候每6分钟通过一辆的汽车的候车时间服从[0，5]上的均匀分布等.

（3）正态分布.若连续型随机变量X的概率密度为

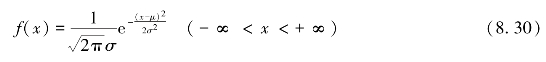
其中μ和σ均为常数，σ＞0，则称随机变量X服从参数为μ、σ2的正态分布[也称高斯（Gauss）分布]，记作：X～N（μ，σ2）.利用泊松积分，可以验证.由微积分的知识可以作出f（x）的图形，形状呈钟形，如图8.11所示.

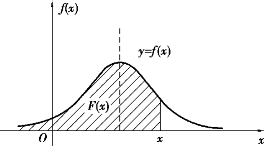
图8.11

正态分布的概率密度曲线具有以下性质：

①关于直线x=μ对称，最大值点是x=μ，在x=μ±σ处有拐点.

②当x→±∞时，曲线以x轴为渐近线.

③固定σ改变μ时，曲线沿x轴平行移动，形状不变；固定μ改变σ时，σ越大，曲线越平坦，σ越小，曲线越陡峭，如图8.12 所示.(www.xing528.com)

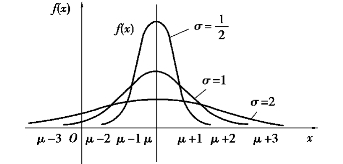
图8.12

若随机变量X～N（μ，σ2），则X的分布函数为

在正态分布中，令μ=0，σ=1，则概率密度变为

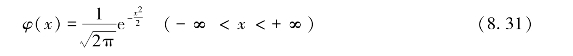
此时的正态分布称为标准正态分布，记作：X～N（0，1）.

φ（x）的图形关于y轴对称，在x=±1处有拐点，在x=0处达到最大值：

φ（x）的图像如图8.13所示.

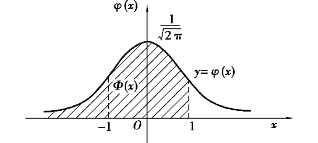
图8.13

标准正态分布的分布函数为：

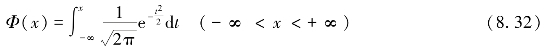
由定积分的换元积分法可以证明，如果X～N（μ，σ2），令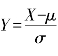，则Y～N（0，1）.此即正态分布的标准化.

下面来看标准正态分布的概率计算.

若X～N（0，1），则由标准正态分布曲线的对称性知：

因此，对于标准正态分布的概率计算，只要解决x≥0的计算就可以了.于是

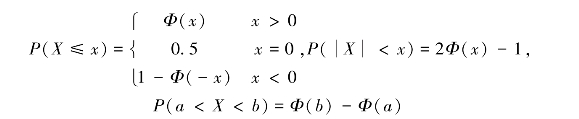
因为Φ（x）不是初等函数，所以靠积分是“积”不出来的，求其函数值非常困难.为计算方便，人们编制了x≥0时的函数值表供查阅，详见附录4.

例8.27　设X～N（0，1），查表求下列各值：

（1）P（X≤1）；（2）P（X≤-1）；（3）P（≤1）；（4）P（-1＜X＜2）；（5）P（X≤3.9）.

解　由附录4可知：

（1）P（X≤1）=Φ（1）=0.841 3；

（2）P（X≤-1）=Φ（-1）=1-Φ（1）=1-0.841 3=0.158 7；

（3）P（≤1）=2Φ（1）-1=2×0.841 3-1=0.682 6；

（4）P（-1＜X＜2）=Φ（2）-Φ（-1）=Φ（2）-[1-Φ（1）]=0.9772-1+0.841 3=0.818 5；

（5）P（X≤3.9）=Φ（3.9）=0.999 95.

例8.28　若X～N（8，0.52），求P（X＞10），P（）.

解　因为X～N（8，0.52），所以，则

P（X＞10）=1-P（X≤10）=1-F（10）=1-Φ（4）≈1-1=0；

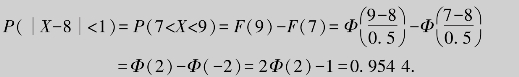
在实际生活中，大量的随机变量都服从或近似服从正态分布.如零件的尺寸、材料的强度、人的身高或体重等，都近似服从正态分布.这些随机变量的分布都具有“中间大两头小”的特点.一般来说，若影响某一数量指标的随机因素很多，而每个因素所起的作用都不太大，则这个指标服从正态分布.正态分布是在实际中应用最广泛、在理论上研究最多的分布之一，故它在概率统计中占据特别重要地位.

下面简单介绍在实际中经常用到的正态分布的3σ原则.

当随机变量X～N（0，1）时，由标准正态分布表可知

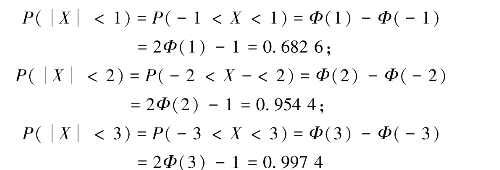
可见，X的取值几乎全在（-3，3）范围内（约占99.74%）.将这些结论推广到一般正态分布，即若随机变量X～N（μ，σ2）时，则有

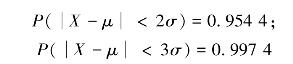
显然的概率是很小的，因此当确认一个数据是来自一般正态分布N（μ，σ2）时，总认为这个数据必须满足不等式

否则就不予以承认，这就是通常所说的2σ或3σ原则.如在质量控制中，常用标准指标值±3σ作两条直线，当生产过程的指标观察值落在两线之外时发出警报，表明生产出现异常.

练习8.2

1.盒中有10个合格品，3个次品，从盒中一件一件地抽取产品检验，每件检验后不再放回盒中，以X表示直到取得第一件合格品为止所需检验次数，求X的分布律，并求P（X＜3）.

2.从某大学到火车站途中有六个路口，假设在各路口遇到红灯的事件相互独立，且概率都是.

（1）以X表示途中遇到的红灯次数，求X的分布律.

（2）以Y表示汽车行驶途中在停止前所通过的路口数，求Y的分布律.

（3）求从该大学到火车站途中至少遇到一次红灯的概率.

3.假设某汽车站在任何长为t（分）的时间内到达的候车人数N（t）服从参数为3t的泊松分布.

（1）求在相邻两分钟内至少来3名乘客的概率.

（2）求在连续5分钟内无乘客到达的概率.

4.设随机变量X的所有可能取值为1，2，3，4，已知P（X=k）正比于k值，求X的分布列及分布函数，并求P（X＜3），P（X=3），P（X≤3）.

5.设离散型随机变量X的分布函数为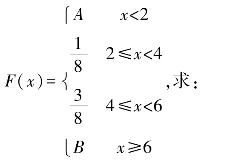

（1）参数A，B；　　　（2）X的分布列.

6.设连续型随机变量X的分布函数为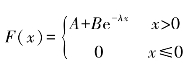，其中λ＞0是常数.求：

（1）参数A，B；　　　（2）P（X≤2），P（X＞3）；　　　（3）X的概率密度.

7.已知X的概率密度为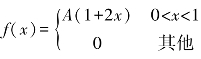，求：

（1）常数A；　　　（2）P（X＞0.5）；　　　（3）分布函数F（x）.

8.某人上班地点离家仅一站路，他在公共汽车站候车时间为X（分钟），X服从指数分布，其概率密度为

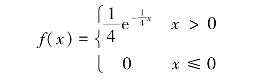
此人每天要在车站候车4次，每次若候车时间超过5分钟，他就改为步行.求此人在一天内步行次数恰好是2次的概率.

9.设X均匀分布于区间[-2，5]，求方程4μ2+4Xμ+X+2=0有实根的概率.

10.设X～N（0，1），分别求b，使：

（1）P（＜b）=0.05；　　　（2）P（X＞b）=0.05；　　　（3）P（X＜b）=0.05.

11.测量某目标的距离时，误差为X（m），且知X～N（20，402），求三次测量中至少有一次误差绝对值不超过30（m）的概率.

12.某汽车加油站的油库每周需油量X（kg）服从N（500，502）分布.为使该站无油可售的概率小于0.01，这个站的油库容量起码应多大?