大学应用数学：离散型随机变量概率分布

1.离散型随机变量的分布列

对离散型随机变量X，它的取值规律除了用分布函数来描述，还可以用分布列来表示.

设xk（k=1，2，…）为离散型随机变量X的所有可能值，而X取值xk的概率为pk，即

则称式（8.17）为离散型随机变量X的概率分布，简称分布列.

离散型随机变量X的分布列也可用表格形式直观表示如下：

由概率的基本性质可知，分布列具有下面两个性质：

（1）非负性：pk≥0，k=1，2，…；

（2）归一性：∑kpk=1.

例8.18　设袋中有10只球，其中有7只白球、3只黑球.现每次从中任取一只球，直到取到白球为止（分不放回和放回两种情形），求所需抽取次数X的分布列.

解　“X=k”表示“前k-1次取到黑球，第k次取到白球”.

（1）不放回取球.X的可能取值为1，2，3，4.

所需抽取次数X的分布列为：

（2）有放回取球.所需抽取次数X的分布列为：

例8.19　某仓库存放一批产品，其中有一、二、三、四等品，分别占总数的70%，15%，10%，5%.现从中任取一个产品，用随机变量X描述产品的等级并画出概率分布图.

解　用“X=k”表示“取到的产品为k等品”（k=1，2，3，4），则X为随机变量，它可以取1，2，3，4这4个可能值，且

P（X=1）=0.7，P（X=2）=0.15，P（X=3）=0.10，P（X=4）=0.05

用表格法表示如下：

其概率分布图如图8.8所示.

图8.8

有了分布列，我们能清楚地看出离散型随机变量X取哪些值，以及取这些值的概率.当然，有了分布列，可以通过下式求出离散型随机变量X的分布函数.

它的图形是在xk处有跃度为pk的右连续的阶梯曲线.虽然用分布函数和分布列都能描述离散型随机变量，但显然用分布列来描述更直观、更简单.

2.几种常见的分布列

（1）两点分布，若随机变量X的分布如下：

即P（X=k）=pkq1-k，（k=0，1），则称随机变量X服从两点分布（也称0-1分布）.(www.xing528.com)

两点分布虽然很简单，但比较常用.当试验只有两个结果且都有正概率时，就确定了一个服从两点分布的随机变量.如前面介绍过的一次抛均匀硬币、一次射击击中与否、一次投蓝投中与否等都是服从两点分布的随机现象.

（2）二项分布.若随机变量X的分布列如下：

则称随机变量X服从参数为n，p的二项分布（也称伯努利分布），记为X～B（n，p）.

显然，P（X=k）＞0，且由二项式定理易知

二项分布的实际背景是前面介绍的n重伯努利概型；两点分布是二项分布当n=1时的特例.

例8.20　从某大学到火车站途中有6个交通岗，假设在各个交通岗是否遇到红灯相互独立，并且遇到红灯的概率都是.

（1）设X为汽车行驶途中遇到的红灯数，求X的分布律.

（2）求汽车行驶途中至少遇到5次红灯的概率.

解　（1）由题意，，于是X的分布律为：

例8.21　某人射击的命中率为0.02，他独立射击400次，试求其命中次数不少于2的概率.

解　设X表示400次独立射击中命中的次数，则X～B（400，0.02），故

由此可见，当n较大时，二项分布的计算较麻烦，可以使用下面的泊松分布来近似计算.

（3）泊松（Poisson）分布.若随机变量X的分布列如下：

其中λ＞0，则称随机变量X服从参数为λ的泊松分布，记为X～P（λ）.

可以证明泊松分布是二项分布的极限分布.当n很大，p很小时，二项分布可近似地看成参数λ=np的泊松分布.

现实生活中有很多随机现象服从泊松分布.例如，在一段时间内电话台的呼叫次数，放射性物质的粒子数，到商店去的顾客数，书中的印刷错误等，都服从泊松分布.

例8.22　设某国每对夫妇的子女数X服从参数为λ的泊松分布，且知一对夫妇有不超过1个孩子的概率为3e-2.求任选一对夫妇，至少有3个孩子的概率.

解　由题意，X～p（λ），且P（X≤1）=P（X=0）+P（X=1）=3e-2，即

e-λ+λe-λ=3e-2⇒λ=2

于是

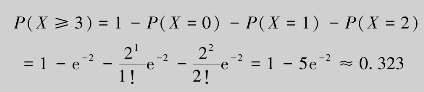
例8.23　在保险公司里有2 500个条件相同的人参加了人寿保险.每个参加保险的人一年交付保险费12元，在一年内死亡时，保险公司即付赔偿金2 000元，设一年内每人死亡的概率为0.002.求保险公司亏本的概率.

解　设一年内死亡的人数为X，则X～B（2 500，0.002）.保险公司亏本等价于2 000X＞2 500×12，即X＞15，因为

而n=2 500很大，p=0.002很小，故可用泊松分布近似计算.因为λ=np=2 500×0.002=5，查附录3得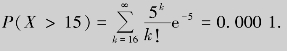

结果表明，P（X＞15）的数值很小，说明该保险公司在现行政策下“亏本”这一事件几乎不会发生.一般地，像这类概率很小的事件称为小概率事件.