一个随机变量，我们不仅要知道它可能取哪些值，而且更重要的是以怎样的概率来取这些值，即它的取值规律.随机变量取值的规律通常用分布函数来描述.
分布函数 设X为一随机变量，称
为随机变量X的分布函数.
由定文可知：分布函数F（x）是定义域为全体实数，值城为[0，1]的普通函数，它的引入使许多概率问题转化为函数问题，这样就可以借助微积分的知识来研究随机事件.
分布函数在点x的函数值就是随机变量落在区间（-∞，x]内的概率.由于对任意实数a＜b，有
P（a＜X≤b）=P（X≤b）-P（X≤a）=F（b）-F（a）
因此由F（x）可求出X在任一区间内取值的概率，从而分布函数F（x）能完整地刻画出不同类型随机变量X的概率分布.
例8.16 “投掷一颗均匀骰子”是随机试验，用随机变量X表示出现的点数.求：
（1）X的取值范围；（2）P（X=1）；（3）P{（X=1）∪（X=2）}；
（4）P（X＞4）和P（X≤4）；（5）P（2≤X＜4）.
解 （1）X的取值范围是{1，2，3，4，5，6}. （2）P（X=1）=
（3）P{（X=1）∪（X=2）}=P（X=1）+P（X=2）=
（4）P（X＞4）=P（X=5）+P（X=6）=
P（X≤4）=1-P（X＞4）=
（5）P（2≤X＜4）=P（X=2）+P（X=3）=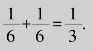
(www.xing528.com)
例8.17 在10件同类型产品中，有3件次品.现任取2件，用随机变量X表示“2件中的次品数”，显然X的可能取值有0，1，2，求随机变量X的分布函数.
解 由古典概率，有
又由F（x）=P（X≤x）（X=0，1，2）得
当x＜0时，{X≤x}是不可能事件，所以F（x）=P（X≤x）=P（ϕ）=0.
当0≤x＜1时，F（x）=P（X≤x）=P（X=0）=
当1≤x＜2时，F（x）=P（X≤x）=P（X=0）+P（X=1）=
当x≥2时，{X≤x}是必然事件，所以F（x）=P（X≤x）=P（Ω）=1.
故随机变量X的分布函数为：
由例8.17可知，分布函数具有如下性质：
（1）0≤F（x）≤1，（-∞＜x＜+∞）.
（2）在整个定义域内，F（x）是x的单调增加函数，即若x1＜x2，则F（x1）≤F（x2）.
（4）F（x）是右连续的，即
根据随机变量取值的情况，可以把随机变量分为两类：离散型随机变量和非离散型随机变量.如果随机变量的所有可能取值是可以一一列举出来的，这样的随机变量称为离散型随机变量.如“打靶环数”“掷一枚均匀骰子点数”“产品抽样检查时出现的次品数”等，都是离散型随机变量.在非离散型随机变量中，最重要的是连续型随机变量，如“分子的运动速度”“候车时的等待时间”“灯泡寿命”等，它们可以取某一区间或整个实数轴上所有的值，这样的随机变量称为连续型随机变量.下面主要研究这两种随机变量及其概率分布.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
