大学应用数学-事件的独立性

1.事件的独立性的定义

一般来说，P（B 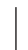A）≠P（B），这表明A的发生影响了B发生的概率.但在特殊情况下，A发生与否并不影响B发生的概率，即有P（B 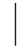A）=P（B）.这时，事件A与事件B具有“独立性”.在P（A）＞0时，由概率的乘法公式及P（B 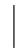A）=P（B）可推出P（AB）=P（A）P（B），由此引入以下定义：

事件的独立性　对于事件A与B，若

则称事件A与B是相互独立的.

由此定义得以下定理：

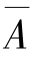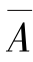定理8.5　（1）必然事件及不可能事件与任何事件独立.（2）若事件A与事件B相互独立，则A与，与B，与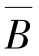中的各对事件也相互独立.（3）当P（A）＞0，P（B）＞0时，下面4个结论是等价的：

①事件A与事件B相互独立.

②P（AB）=P（A）P（B）.

③P(B)= P(B|A)

④P(A)= P(A|B).

必须注意的是：在实际应用中，通常是根据事件的实际意义和相互关系来判断是否相互独立.

一般来说，如果n个事件A1，A2，…，An中任意一个事件发生的可能性都不受其他事件发生与否的影响，则可判断这n个事件相互独立，且

下面的例子可以帮助我们区分两事件相互影响和相互独立的意义.

例8.12　某公司生产的一批灯泡：在被检查的100个灯泡中，有两个是坏的.某人从这100个灯泡中随机抽取两个灯泡，抽出第一个之后不放回，再抽第二个，则连续抽到两个坏灯泡的概率是多少?若他抽出第一个后，将其放回，再随机抽第二个，则连续抽到两个坏灯泡的概率是多少?

解　设A={抽到第一个是坏灯泡}，B={抽到第二个是坏灯泡}，则AB={抽到两个都是坏灯泡}.

（1）抽后不放回

由于A发生，余下的99个灯泡中，只有一个是坏的，因此

（2）抽后再放回.此时，A发生与否不影响B的发生，第一次和第二次抽取都是从有两个坏灯泡的100个灯泡中抽取一个，因此是相互独立的，并且

例8.13　假定有奖储蓄1万张为一组，奖号由5位数字A5A4A3A2A1组成，其中Ai（i=1，2，3，4，5）是0，1，2，…9中任一个数字.设一等奖1个，中奖号码由后面四位数字决定；二等奖10个，中奖号码由后面三位数字决定；三等奖100个，中奖号码由后面两位数字决定；四等奖1 000个，中奖号码由后面一位数字决定.今任意购买1张奖券，中各等奖的概率是多少?

解　设Ai（i=1，2，3，4，5）表示事件“抽到数字Ai”，由于抽取各位中奖数字是独立进行的，因此事件Ai（i=1，2，3，4，5）相互独立，并且

依题意，中一等奖的事件为A4A3A2A1；中二等奖的事件为A3A2A1；中三等奖的事件为A2A1；中四等奖的事件为A1.它们的概率分别为：

2.伯努利概型

在概率初步中，只考虑两个可能结果A和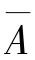的随机试验，称为伯努利试验.将伯努利试验独立地重复n次，称为n重伯努利试验；描述n重伯努利试验结果的数学模型，称为n重伯努利概型，简称伯努利概型（也称为独立试验序列模型）.例如，将一枚均匀硬币重复抛20次，观察出现正反面的试验，属于伯努利概型；而将一颗骰子重复掷20次，观察出现点数的试验，由于试验的结果不止两种，因此不属于伯努利概型.

对于伯努利概型，我们主要研究n次试验中事件A发生k次的概率.先看下面的例子：

例8.14　设有一批产品，次品率为p.现进行有放回的抽取，问任取4次后，发现其中恰有2件次品的概率是多少?(www.xing528.com)

解　设Ai ={第i次抽到次品}（i=1，2，3，4），则={第i次抽到正品}.在4次试验中，抽得2件次品的可能情况有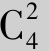=6种：

以上各种方式中，任何两种方式都是互斥的.因此在4次试验中，恰抽得2件次品的概率是

由于抽得次品的概率都是一样的，即P（A__i）=p，且各次试验相互独立，于是有

同理有

于是P4（2）=p2（1-p）4-2+p2（1-p）4-2+…+p2（1-p）4-2=

推广到一般情形，便有下面的伯努利定理.

伯努利定理　如果在一次试验中，事件A发生的概率为p（0＜p＜1），则在n重伯努利试验中，事件A恰好发生k次的概率为

例8.15　一条自动化生产线上产品的一级品率为0.6，现从中随机抽取10件检查，求：

（1）恰有2件一级品的概率.（2）至少有2件一级品的概率.

解　本题中的抽样方法是不放回抽样，但由题意知产品的数量很大，而抽取数量相对较小，因此可作为有放回抽样来近似处理.所以可以将检查10件样品是否是一级品看成是10重伯努利试验.

设Ai={恰有i件一级品}（i=0，1，…，10），B={至少有2件一级品}，则

伯努利概型是在同样条件下进行重复试验的概率模型，是概率论研究的最早模型之一.前面提到过的随机现象的统计规律性，只有在这种重复试验中才会显示出来.概率论中的一些重要结论，起初主要是通过对伯努利概型进行研究得到的，而且伯努利概型在产品质量检验及群体遗传学等方面有着广泛的应用.

练习8.1

1.一工人生产了4件产品，以Ai表示他生产的第i件产品是正品（i=1，2，3，4），试用Ai（i=1，2，3，4）表示下列事件.

（1）没有一件产品是次品；　　（2）至少有一件产品是次品；

（3）恰有一件产品是次品；　　（4）至少有两件产品不是次品.

2.对飞机进行两次射击，每次射一弹，设事件A={第一次击中飞机}，B={第二次击中飞机}，C={恰有一弹击中飞机}，D={至少有一弹击中飞机}，E={两弹都击中飞机}.

（1）试用事件A、B表示事件C、D、E.

（2）C与E是互逆事件吗?为什么?

3.在1 500件产品中有400件次品，1 100件正品.任取200件，求：（1）恰好有90件次品的概率.（2）至少有两件次品的概率.

4.设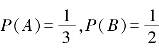，在下列三种情况下求的值：

（1）AB=∅；　　　　　　（2）A⊂B；　　　　　　（3）P（AB）=.

5.设A、B是两个事件，

6.射手对目标独立射击5发，单发命中的概率为0.6，求：（1）恰好命中2发的概率.（2）至多命中3发的概率.（3）至少命中1发的概率.