大学应用数学：概率运算高效技巧

1.加法公式

定理8.1　设事件A与事件B互不相容，则

推论8.1　若事件A1，A2，…，An两两互不相容，则

推论8.2　对于任意两事件A，B，有

特别地，若B⊂A.则

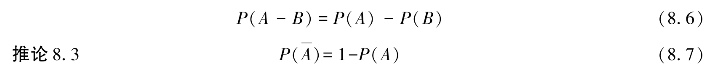
例8.7　某人打靶，命中10环的概率为0.40，命中8环或9环的概率为0.45，求最多命中7环的概率.

解　设A={命中10环}，B={命中8环或9环}，C={最多命中7环}，则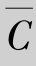={命中的环数大于7环}.因为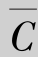=A+B，且A与B互不相容，所以

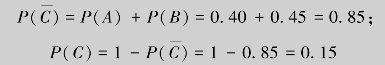
即最多命中7环的概率为0.15.

定理8.2　对于任意两事件A，B，有

例8.8　设某种玩具可有S1，S2，S3，S4四种式样.每种式样又有白（Y1）、红（Y2）、黄（Y3）三种颜色，设在10 000件玩具中按式样和颜色分类的数量如表8.3所示.现从中随机抽出一件，问：（1）抽到S1式样的概率是多少?（2）抽到白色的概率是多少?（3）抽到既是式样S1又是白色的概率是多少?（4）抽到式样S1或白色的概率是多少?

表8.3

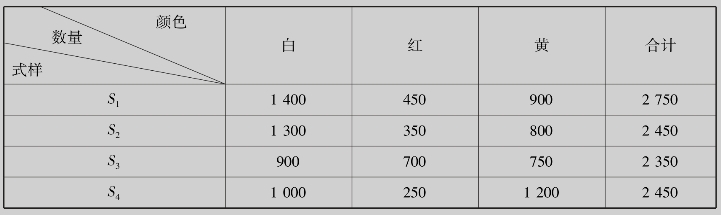
解　令S1={抽到S1式样}，Y1={抽到白色的}.根据表9.3中数据，有

（4）根据加法公式，有P（S1∪Y1）=P（S1）+P（Y1）-P（S1Y1）=0.275+0.46-0.14=0.595.

这个例子可以帮助我们更加直观地理解上述加法公式.因为表中的1 400件既是式样S1又是白色的玩具数，它既包括在S1的2 750件中，又包括在白色的4 600件中，在计算P（S1）、P（Y1）时，重叠应用了这1 400件，因此加法公式中要减去这重叠部分的概率.

2.乘法公式

再看例8.8，由表8.3，已经知道

如果要问：在式样S1已给定的条件下，随机抽取一件为白色的概率有多大?这是一个在S1已发生的条件下，求事件Y1的概率，称为条件概率，并记作

此处，Y1与S1之间的竖线读作“给定”，而整个记号读作“给定S1时，Y1的概率”.由表8.3知，S1有2 750件，其中Y1（白色）占1 400件，故有

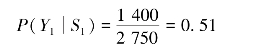
可用另外的一种方法来计算这一概率.由，得2 750=10 000P（S1）；

由P（S1Y1）=，得1 400=10 000P（S1Y1）.所以

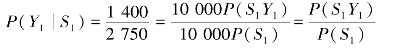
这样就得到条件概率的一般表达式：

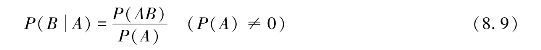
或(www.xing528.com)

上式也可改写成

即两个事件乘积的概率等于一个事件的概率与另一个事件在前一事件发生下的条件概率的乘积.式（8.10）称为乘法公式.

乘法公式可以推广到n个事件乘积的情形：

例8.9　在一次对一年级学生上下两学期学习成绩的统计调查中发现：上下两学期均得优的占被调查学生的5%，仅上学期得优的占7.9%，仅下学期得优的占8.9%，求：

（1）已知某学生上学期得优，估计下学期得优的概率.

（2）已知某学生上学期没得优，估计下学期得优的概率.

（3）上、下两学期均未得优的概率.

解　设A={上学期成绩得优}，B={下学期成绩得优}.由题意知，P（AB）=0.05，P

又由，得

于是

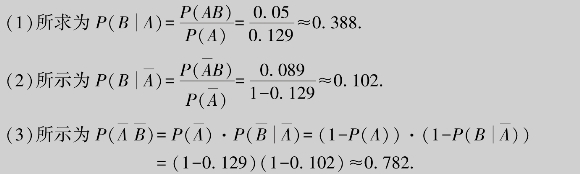
3.全概率公式

把一个复杂事件分解为一组简单事件之和，再通过加法公式、乘法公式去求概率，这是求解某些复杂事件概率的有效方法，将这种解题思路一般化，就得到全概率公式.

定理8.3　如果事件A1，A2，…，An构成一个完备事件组，则对任何一个事件B，有

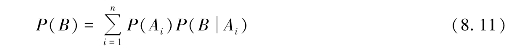
式（8.11）称为全概率公式，它指的是B的全部概率.

例8.10　市场上有甲、乙、丙三家工厂生产的同一品牌产品，已知三家工厂的市场占有率分别为25%，25%，50%，且三家工厂的次品率分别为2%，1%，3%，试求市场上该品牌产品的次品率.

解　设A1={产品为甲工厂生产}，A2={产品为乙工厂生产}，A3={产品为丙工厂生产}，B={产品为次品}；显然，A1，A2，A3构成一个完备事件组.依题意，有

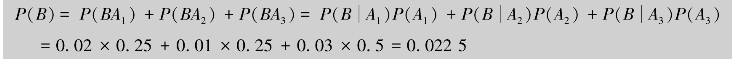
4.贝叶斯公式

全概率公式给出了事件B随着事件A1，A2，…，An中某一个发生而发生的概率.反过来，如果知道事件B已经发生，但不知道它是由A1，A2，…，An中哪个事件发生而随之发生的，这样便产生了在事件B已经发生的前提下，求事件Ai（i=1，2，3，…，n）发生的概率，对此有下面的定理.

定理8.4　若A1，A2，…，An构成一个完备事件组，则对任一事件B，当P（B）＞0时，有

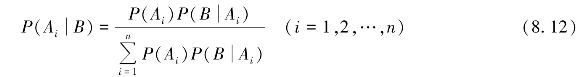
式（8.12）称为贝叶斯公式，也称为逆概率公式.

例8.11　继续讨论例8.10，若已知某件产品为次品，问：它由甲、乙、丙工厂生产的概率各为多少?哪个工厂生产该次品的可能性最大?

解　由于例8.10已经求出P（B）=0.022 5，故直接求得：

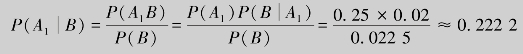
同理

因为，所以丙工厂生产该次品的可能性最大.