匈牙利法解决最佳分配方案，并减元法简化矩阵

匈牙利法为匈牙利数学家D.König提出.该方法简单直观地给出了求最佳分配方案的思路和结果.在此仅举例说明解法.

例7.10　有四种零件分配给四台机床加工，各机床性能不同，加工各种零件的成本也不相同（见表7.10）.问如何进行合理的一一分配，才能使总成本最小.

表7.10

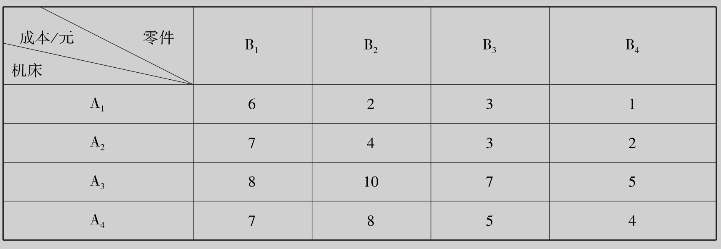
解　（1）列出消耗矩阵：

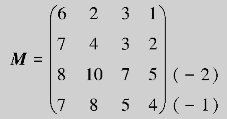
（-6）（-2）（-3）（-1）

（2）通过减元法（各行各列减去其最小元），得简化矩阵（指各行各列均含0元）：

（3）用尽可能少的纵横直线覆盖所有0元.若线数＜矩阵阶数，则须做调整.这里因线数3＜矩阵阶数4，故对M1做调整.

（4）先求调整量θ=min{未覆盖元}，调整方法为：未覆盖元-θ，交叉覆盖元+θ.这里θ1=1，调整后得新简化阵：

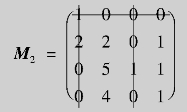
返回（3）划线检验，因线数3＜矩阵阶数4；转入（4）调整，θ2=1，调整后得新简化阵：

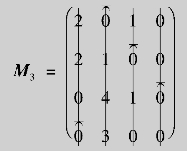
返回（3）划线检验，因线数=矩阵阶数，转入下一步.

（5）选出M3中不同行不同列的0元，令选中位置xij=1，其他位置xij=0，得最优分配阵：

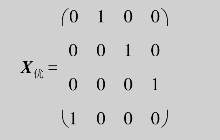
此时min S=7+2+3+5=17.

必须注意的是：最优分配阵可能不唯一，但最优值必唯一.

如果分配问题提供的是效率阵，则必须用缩减法化为消耗阵，然后用匈牙利法求解.

例7.11　三个人分配三个职务，其工作效率如表7.11所示，求最佳分配方案.

表7.11

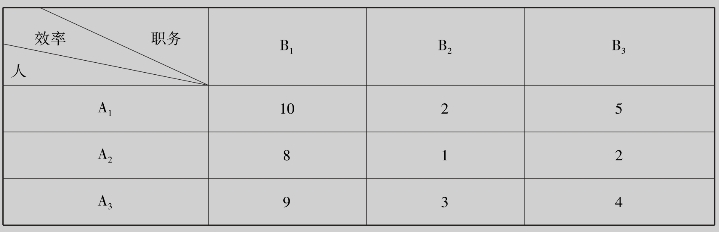
解　（1）将效率阵通过缩减法化为消耗阵（方法是用最大元10减去每个元）：

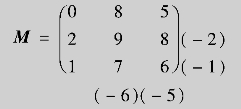
（2）用减元法得简化阵：

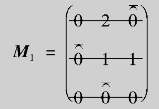
（3）划线检验：线数=阶数3.

（4）选出M1中不同行不同列的0元，构造最优分配阵：

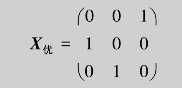
此时max S=8+3+5=16.

如果出现人多事少或人少事多的情况，可以用添加虚拟人或事的办法.即在消耗阵中添加虚拟行或列（其元素全为0），使之成为一个方阵，化为一一分配问题.

匈牙利法求解一一分配问题的步骤如图7.13所示.

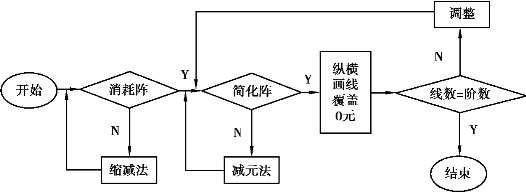
图7.13

练习7.4

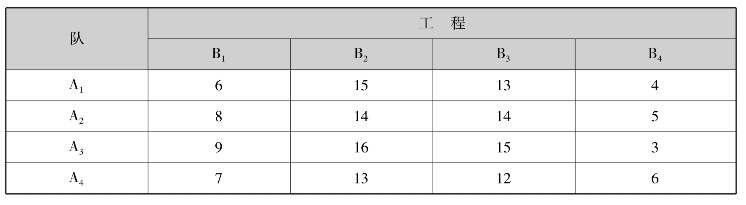
用匈牙利法求解分配问题：四个工程队和四项工程，各队投标各工程的费用如表7.12所示，问如何进行一一分配，使投标的总费用最省?

表7.12

第7章自测题

1.填空题

（1）线性规划问题就是求一组变量，在满足________约束条件下，使________目标函数达到最大或最小的问题.

（2）线性规划问题模型中满足约束条件的解称为________，使目标函数达到最优的解称为________.

（3）使用单纯形法求解线性规划问题，必须将线性规划问题的数学模型________.(www.xing528.com)

（4）单纯形法的基本思想是________________________.

（5）在运输问题中，如果一个流向图中既无________又无________，则为最优流向图.

2.建立下列问题的数学模型

（1）某煤矿生产褐煤和无烟煤.设采煤、选煤和洗煤三道流水线每天运行时间分别不能超过12小时、10小时和8小时.生产每百吨褐煤需采煤3小时，选煤3小时，洗煤4小时，可获利4 000元；生产每百吨无烟煤需采煤4小时，选煤3小时，洗煤2小时，可获利3 000元.问如何安排生产计划使每日获最大利润?

（2）有一批长度规格为180 cm长的钢管.今需三种不同长度的管料，需量为：70 cm长度100段，52 cm长度150段，35 cm长度100段，向如何合理下料使总的余料最少?

3.使用单纯形法求解下列线性规划问题

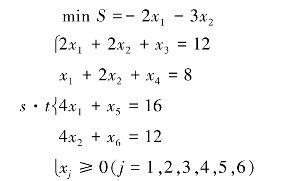
4.求下列交通图（见图7.14）的最优运输方案

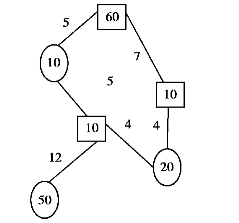
图7.14

5.应用题

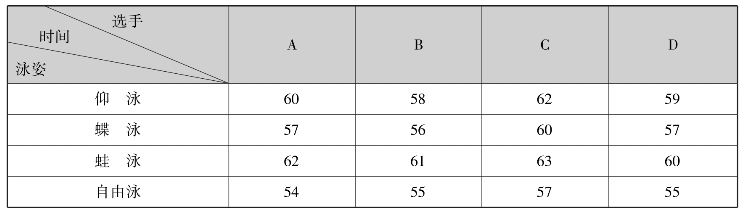
一个四人组成的4×100米混合游泳接力队，已知各人四种泳姿的水平如表7.13所示，问如何组合，才能发挥总体最佳水平?

表7.13

思政　阅读材料之七

数学与人工智能

人工智能（Artificial Intelligence），英文缩写为AI.他是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学.

人工智能是一门极富挑战性的科学，从事这项工作的人必须懂得计算机知识、心理学和哲学.人工智能是包括十分广泛的科学，由不同的领域组成，如机器学习、计算机视觉等，总的说来，人工智能研究的一个主要目标是使机器能够胜任一些通常需要人类智能才能完成的复杂工作.

“人工智能的基石是数学，没有数学基础科学的支持，人工智能很难行稳至远.”在中国科学院院士、西安交通大学教授徐宗本看来，目前人工智能所面临的一些基础问题，其本质是来自数学的挑战.

在由联合国教科文组织和中国工程院联合主办的以“大数据与知识服务”为主题的联合高端研讨会上，徐宗本在《AI与数学：融通共进》的主题报告上说.

数学家眼里的人工智能是什么?

徐宗本给出的答案简洁明了：当下主要指机器学习.

如果给这个名词赋予一个说明，他认为这是人或者智能体，通过与环境的交互来提升自身行为和解决问题能力的智能化操作.“机器学习是把这种智能形式化为数学公式，转换成计算机可以操作的算法和软件.”

进一步说，人工智能实际上是一个将数学、算法理论和工程实践紧密结合的领域.将其扒开来看，就是算法，也就是数学、概率论、统计学、各种数学理论的体现.

不过徐宗本认为，作为人工智能基石的数学，还存在五大核心问题待解，而这也是制约人工智能进一步发展的“绊脚石”.

第一是大数据的统计学基础.

人工智能和大数据是一对孪生姐妹.人工智能更多指应用模式，强调与领域知识的结合.大数据是最底层的信息技术，强调机器和机器、机器与人之间的内容交互与理解.但是当前，分析大数据的统计学基础面临被颠覆，应用于复杂大数据分析的极限理论、统计推断方法、真伪判定等数学基础都尚未完全建立起来.

第二是大数据计算基础算法.

一般而言，理解和分析大数据都是通过数据处理或数据分析来实现的，而无论是数据处理还是数据分析最终都化归到求解一系列基本的数学问题，像线性方程组求解、图计算、最优化计算、高维积分等.不过，这些看似早已解决的问题在大数据情形下却成了“拦路虎”.

为此，他以旅游为例，打了一个生动的比方来解释这种挑战.“比如从西安到北京，怎么走最近?过去地图分辨率不高，根据普通的地图可以获取基本的路线.但现在大数据背景下地图的分辨率越来越高，不可能一次就给你涵盖西安至北京之间全部城市与道路的数据，只能一次一次地分别给其中某些城市之间的道路信息.如何在西安就知道到达北京需要多少时间，怎样走最近?要带多少钱?现在的机器还回答不了这些问题.这就是分布式图信息环境下图计算基础算法没有解决的原因.”

第三是深度学习的数学理论.

徐宗本认为，这个问题在当下尤为关键.新一轮的人工智能多以深度学习为基本模型，然而深度学习的设计基础在哪?什么样的结构决定了什么样的性能?这些基本的理论问题还没有解决.正是这个原因，现在的人工智能还得靠“人工”来换“智能”，这也是造成当下“人工智能=人工+智能”的缘由.

第四是非常规约束下的最优运输.

人工智能的很多问题都可归纳为两个领域数据打通问题，即让两个对象在满足某一个特定的不变量情况下互相转移.“比如中英文互译，他就是在保持语义的情况下将中文数据转换成英文数据.”

如果应用到现实，徐宗本畅想，将医院的CT和核磁共振图像相互转移或能很好地解决医疗诊断的信息不足问题.“因为照的是同一个人，这里人就是不变量.要解决这些问题，建立特定约束下如何实现最优传输的数学理论与方法是基本的.”

第五是关于学习方法论的建模与函数空间上的学习理论.

徐宗本表示，研究生阶段学到的机器学习理论，需上升到学习方法论学习的阶段.

“从数学上说，无论函数空间上的学习理论怎么建立，本质是要适应不同的任务.由于任务本身是函数，是无穷的，那么就需要把过去机器学习中对样本、数据的选择、泛化，推广到对任务的选择、泛化上去.”

如果辩证地看待数学和人工智能的关系，相辅相成可能是其最好的诠释.徐宗本表示，不仅数学可为人工智能提供基础，人工智能也可为数学研究提供新的方法论.

“比如解偏微分方程，过去人们可能会使用计算机，现在用人工智能可以做得更好.”他认为，让数学中的模型方法与人工智能的数据方法结合，可将机器的深度学习应用得更加精明.

面对如今发展如火如荼的人工智能产业，这位院士也给出了自己对从业者的希冀.

“人工智能想要做得好，要靠数学问题尤其是算法的解决.”徐宗本再次强调，从业者应潜心从基础研究抓起，使我国的应用场景优势真正转化为技术优势和产业优势.