图上作业法：提升大学应用数学实践成效

运输问题的图上作业法是我国数学工作者与现场工作者的创造，在实际应用中方法简便、直观易学.

设每单位物质的运价与距离成正比，为方便起见，直接用cij表示发点Ai到收点Bj间的距离.在图上发点标圆框，收点标方框，将发量或收量记在框内.各点之间若直接相通，用连线相接，并将距离标在连线旁，称为边长.若安排沿连线某方向有运输量（称为流量），则将此量打上括号及流向，标在连线旁，如图7.1所示.

图7.1

标明发点、收点及其发量收量和各点之间连线及其距离的图，称为交通图.标明流量及其流向的交通图，称为流向图.

1.对流与迂回

出现物质在同一线路上往返运输的现象，称为对流，如图7.2所示.

图7.2

克服对流的方法是在对流边上“大流减小流，方向从大流”.图7.2在B1B2边上出现对流，改造后的流向图如图7.3所示.

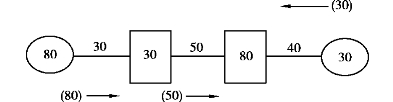
图7.3

流向图中若构成回路（圈），如图7.4所示，从Ai到Bj有两条路，长度分别为c1和c2，且c1＞c2，若安排流量xij从长边c1走，即走长线的现象出现，称为迂回.

令圈长c=c1+c2，因，故走c1线产生迂回；改走c2线后，因，即克服了迂回.

若一个圈上有多个收点和发点，我们将物质在圈上沿顺时针方向流动的边长之和记为c-，沿逆时针方向流动的边长之和记为c+，当流向图中出现c+或c-超过圈长之半时，称为迂回.如图7.5所示，因c=13，c+=7，c-=4，其中，故有迂回.

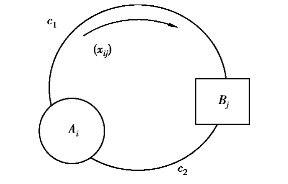
图7.4

图7.5

出现迂回，在圈上要调整，先选取调整量θ，令θ=min{迂回向流量}；调整方法为：迂回向流量-θ，其他边流量+θ.本例中θ=min{30，10}=10，调整后的流向图如图7.6所示.此图中c+=3，c-=6，均小于，克服了迂回.

一个流向图中既无对流又无迂回，即为最优流向图，也称最优运输方案.图7.6为最优流向图，运费min S=200.

2.无圈交通图的图上作业法

根据就近运输的原则，即“端点出发，逐点满足，避免对流，结点平衡”.

例7.8　如图7.7所示为一个三发点三收点的无圈交通图.根据上述口诀作业，所得流向图即为最优方案，总运费达min S=1 230.(www.xing528.com)

图7.6

图7.7

3.含圈交通图的图上作业法

先在圈上任破去一边成无圈图，根据无圈图作业法得一流向图，然后恢复破去的边，即为原含圈的初始流向图.接着检验图上是否出现迂回，若无迂回，即为最优流向图；否则进行调整，直到圈上无迂回，得最优方案.

例7.9　如图7.8所示，一个含单圈的交通图，先破去一边，根据无圈图上作业法得一流向图；然后补上破去边在圈上检验.c=7+4+4+5+5=25，c+=4，c-=4+5+5=14，因，故在圈上顺时针方向出现迂回.

选取调整量θ=min{10，50，60}=10，在圈上调整后得一新流向图（见图7.9）.经检验，c+=4+7=11，c-=5+5=10，因均小于，故圈上c无迂回.此图即为最优流向图，min S=1 200.

必须注意的是：（1）若圈上有迂回，经一次调整后仍有迂回，可继续进行调整.（2）若交通图为多圈情况，首先在每个圈上破去一边成无圈图进行作业；然后补上破去边，在每个圈上进行检验和调整，直至每个圈均无迂回现象，方得最优流向图.

图7.8

图7.9

我们将运输问题的图上作业法的步骤画成程序框图如图7.10所示.

图7.10

练习7.3

求图7.11和图7.12所示交通图的最优流向图.

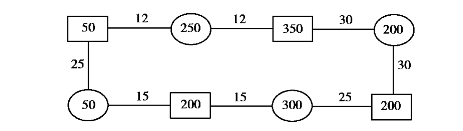
图7.11

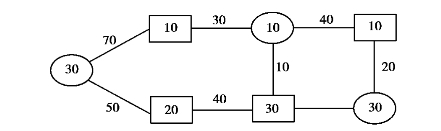
图7.12