单纯形法步骤简介｜大学应用数学

总的来说，单纯形法分为两大步，第一步是求一个可行基；第二步是从该基出发，经过有限次的换基而得到最优基和最优解.

为了简便起见，单纯形法可在表上进行，把这种表称为单纯形表.下面给出单纯形法的具体计算步骤.并仍以例7.4为例进行说明.

1.确定初始可行基、基变量及非基变量

在例7.4中，取初始可行基为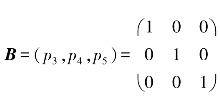，基变量为x3，x4，x5，非基变量为x1，x2.

2.填写单纯形表

表中第一列填写基变量；第二列填写约束方程组右端的常数项b；第一行依次填写所有变量；最后一行填写目标函数的系数；第一列与最后一行的相交处填写c（c表示目标函数的系数矩阵）；第二列与最后一行的相交处填写0；其余部分是约束方程组的系数矩阵A.只要令非基变量为零，便可得对应于基B的基本可行解X（0）.

例7.4的单纯形表如表7.4所示.

令x1=x2=0，有基本可行解X（0）=（0，0，8，7，3）T.

表7.4

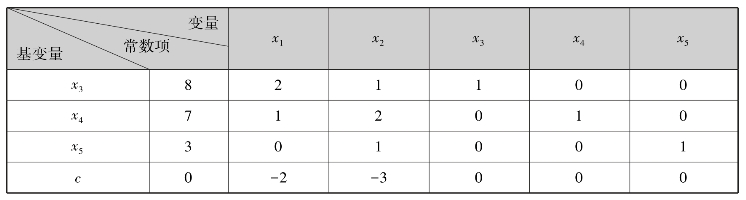
3.检验

为检验X（0）是否为最优解，利用行的初等变换，将最后一行目标函数的基变量的系数化为零，如果非基变量的系数（称为检验数，记为λi）皆非负，则X（0）是最优解，计算终止.否则X（0）不是最优解，转入下一步.

在例7.4中，由于λ1=-2＜0，λ2=-3＜0，所以X（0）不是最优解.

4.换基

（1）确定入基变量、离基变量及主元素.取所有值为负数的检验数λj的最小者，记为λj﹏，其所在列称为主列.如果主列中有正数，则该列对应的非基变量称为入基变量；如果主列中所有元素皆非正，那么目标函数无下界，此时线性规划无最优解，算法终止；否则，在主列中必有正元素，找出所有正元素，然后分别去除常数项b中对应元素，商中最小者所在的行称为主行，主行对应的基变量就称为离基变量，离基变量所在行（即主行）与入基变量所在列（即主列）相交处的元素称为主元素，用记号□框住.

在例7.4中，因为检验数λ2=-3＜λ1=-2，所以将λ2记为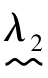，第二列为主列，该列中有正数，因此变量x2换作入基变量.又因为，故常数项为3的行为主行，与该行对应的原基变量x5成为离基变量.主行与主列相交处的主元素为1，如表7.5所示.

（2）根据主元素进行旋转计算.将主行离基变量换成入基变量，利用行初等变换，将主列中主元素化为1，其余元索均化为0，得新基B1、新目标函数及新的基本可行解X（1），用新表反映出来，第一次迭代完成.对应例7.4的情况如表7.6中的迭代1所示，这里新基B1=（p2，p3，p4），对应于基B1的基本可行解为X（1）=（0，3，5，1，0）T.

表7.5

续表

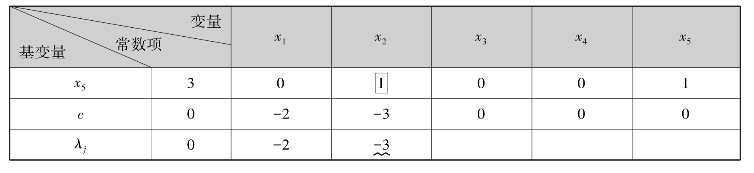
表7.6

（3）对基本可行解X（1），转向步骤3，经检验后，或终止计算，或再施行换基迭代，使目标函数值逐渐减小，经过有限次迭代之后，算法终止于一个最优解上.

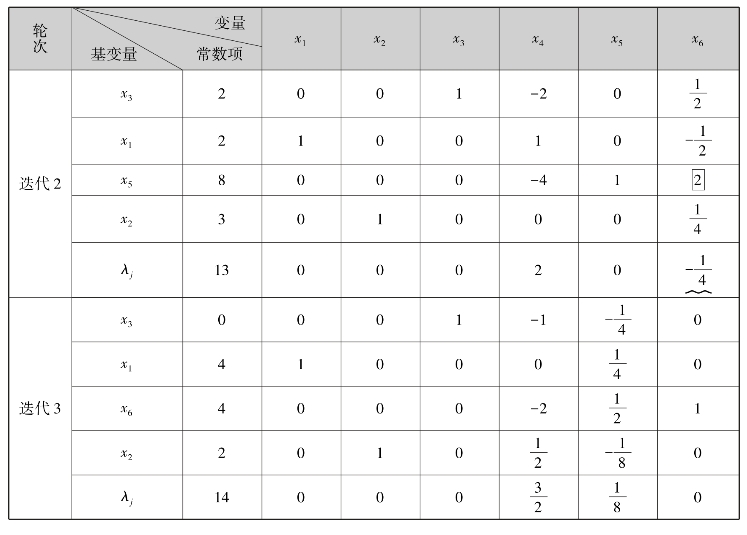
对例7.4来说，由表7.6知，λ1=-2＜0，所以X（1）不是最优解，重复上述做法，选x1为入基变量，x4为离基变量，主元素为1，根据主元素旋转计算后，得新基B2=（p3，p1，p2），新基变量x3，x1，x2及基本可行解X（2）=（1，3，3，0，0）T.如表7.6中迭代2所示.

因为λ5=-1＜0，所以X（2）还不是最优解.再重复上述方法，作换基迭代，得表7.6中迭代3.

由于此时所有检验数皆非负，所以迭代3中新基对应的基本可行解X（3）=（3，2，0，0，1）T为最优解.此时最优值为=-2×3-3×2=-12，从而原线性规划问题最优解值max S=1.

单纯形法掌握熟练后，可略去中间叙述，把所有单纯形表集中到一张表上，然后将算法直接在表上进行，从而使计算过程简单化.

例7.5　用单纯形法求解线性规划问题.

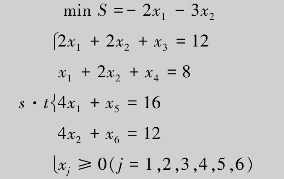(www.xing528.com)

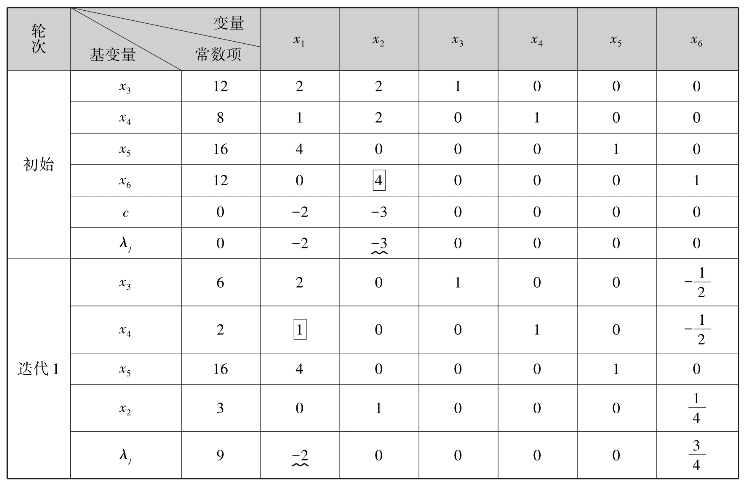
解　因为，所以选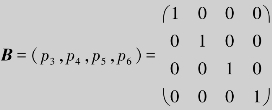为初始基，列出对应单纯形表，并将算法在表7.7上实现.

表7.7

续表

例7.6　用单纯形法求解线性规划问题.

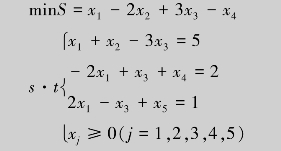
解　这里c=（1，-2，3，-1），b=（5，2，1）T，X=（x1，x2，x3，x4，x5）T，约束方程系数矩阵

选择非奇异子阵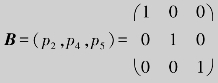为初始基，得初始基变量x2，x4，x5和非基变量x1，x3.列出单纯形表如表7.8所示，并在表上进行换基迭代.

表7.8

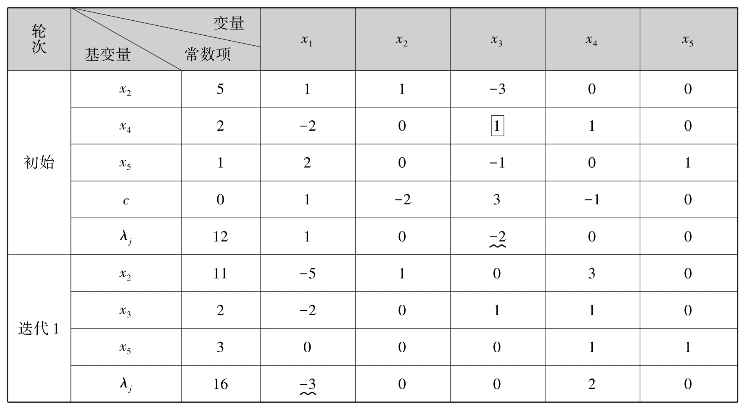
由于检验数λ1=-3＜0，其所在的主列（即第1列）无正元素，故该问题无最优解.

例7.7　用单纯形法求解线性规划问题.

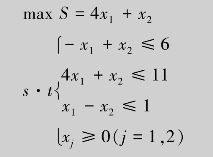
解　引进松弛变量x3，x4，x5，将问题化为标准形：

这里c=（-4，-1），b=（6，11，1）T，X=（x1，x2，x3，x4，x5）T，约束方程系数矩阵

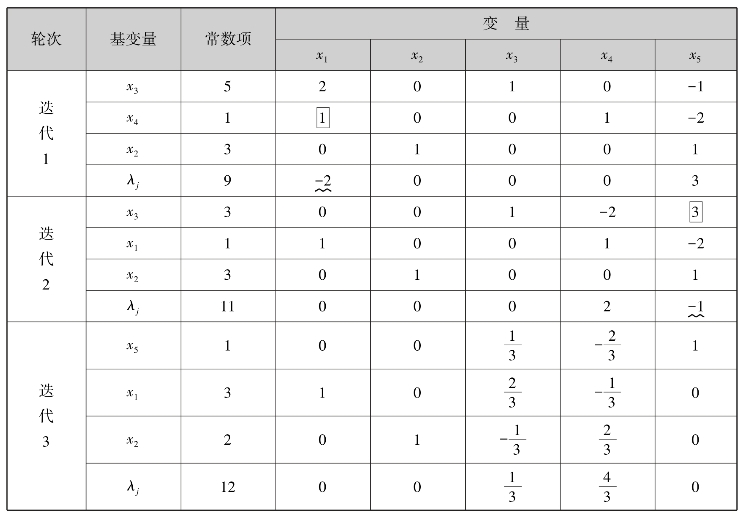
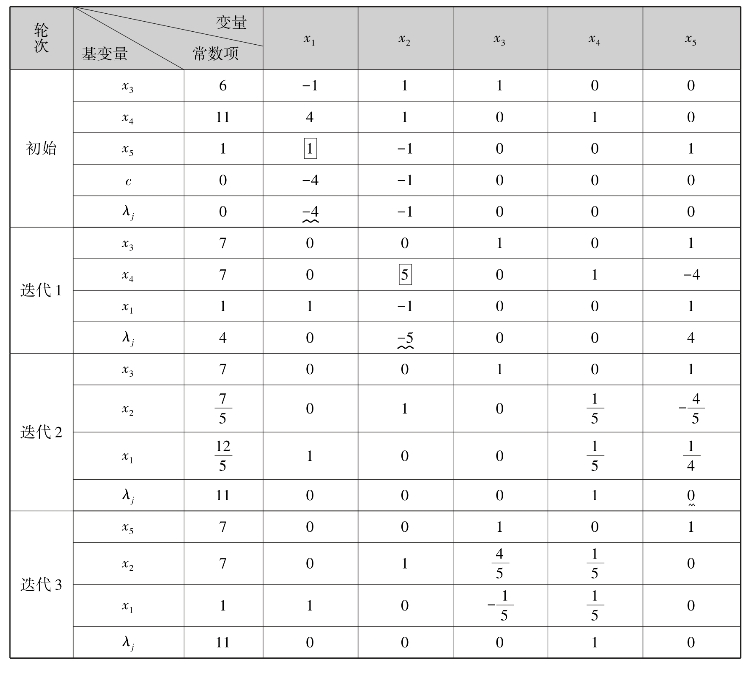
选择非奇异子阵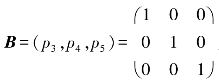为初始基，得初始基变量x3，x4，x5和非基变量x1，x2.列出单纯表如表7.9所示，并在表上进行换基迭代.

因为在表7.9中第二次迭代后，检验数已全部非负，所以有最优解X（2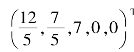）=，相应的最优值min S～=-11，从而原问题的最优解是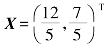，最优值为

由于在迭代2中有非基变量x5的检验数为零，这说明存在另一种换基的选择——x5可成为入基变量，于是继续迭代3，得另一个最优解X（3）=（1，7，0，0，7）T.此时，原问题的最优解仍为11.同理，因为迭代3也有非基变量（如x3）的检验数为零，可选择该非基变量为入基变量，又可进行换基迭代，从而求出又一个最优解……如此进行下去，可知这个问题有无穷多个最优解，且最优值均为11.

表7.9

一般来说，对于一个线性规划问题，如果其最优解对应的单纯形表中有非基变量对应的检验数为零，则问题的最优解可能不止一个，而一旦求得一个最优解，那么最优解必有无穷多个.

练习7.2

1.用单纯形法求解下列线性规划问题.

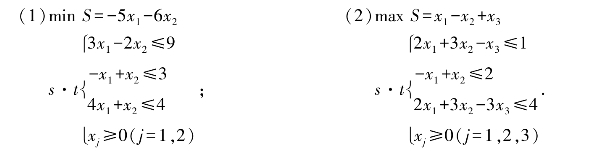
2.某厂生产甲、乙两种产品，生产甲种产品每件要消耗煤9吨，电力4千瓦，使用劳动力3个，获利70元；生产乙种产品每件要消耗煤4吨，电力5千瓦，使用劳动力10个，获利120元.有一个生产日，这个厂可动用的煤是360吨，电力是200千瓦，劳动力是300个，问应该如何安排甲、乙两种产品的生产，才能使工厂在当日的获利最大，并问该厂当日的最大获利是多少?