1.几个基本概念
设有线性规划问题minS=cX
其中c=(c1,c2,…,cn),X=(x1,x2,…,xn)T,b=(b1,b2,…,bm)T,
(1)基、基变量与非基变量.矩阵A中任意一个m阶的非奇异子阵B称为线性规划问题(7.2)的一个基,不妨设
那么Pj对应的变量xj(j=1,2,…,m)称为基变量,而其余的变量xm+1,xm+2,…,xn称为非基变量.
(2)基本解、基本可行解与可行基.对于基B=(p1,p2,…,pm),在AX=b中,令非基变量全为零,可唯一地确定出一个解
X=(x1,x2,…,xm,0,…,0)T
称为线性规划问题(7.2)的一个基本解.
如果基本解X又满足非负限制,即X≥0,则X被称为基本可行解,基本可行解对应的基称为可行基.
2.解法举例
例7.4 求解线性规划问题.
解 首先引进松弛变量x3≥0,x4≥0,x5≥0,将原线性规划问题转化为标准形式:
因为约束方程的系数矩阵为
显然子阵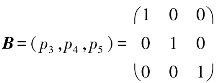 是非奇异的,从而是线性规划问题的一个基.于是变量x3,x4,x5成为对应于此基的基变量,变量x1,x2就是非基变量.
是非奇异的,从而是线性规划问题的一个基.于是变量x3,x4,x5成为对应于此基的基变量,变量x1,x2就是非基变量.
令x1=x2=0,由方程组(7.3)得到问题的一个基本解X(0)=(0.0,8,7,3)T.(https://www.xing528.com)
由于基本解X(0)满足非负限制条件,所以X(0)是一个基本可行解,相应的基B成为可行基,目标函数值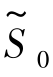 =-2×0-3×0=0.显然这个解不是最优解.
=-2×0-3×0=0.显然这个解不是最优解.
为寻求更优解,考察目标函数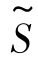 =-2x1-3x2,由于非基变量x1,x2的系数都是负数,x1,x2中只要有一个取正值,
=-2x1-3x2,由于非基变量x1,x2的系数都是负数,x1,x2中只要有一个取正值,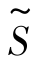 的值就会减小,又因x2的系数的绝对值比x1的大些,改变x2的值对
的值就会减小,又因x2的系数的绝对值比x1的大些,改变x2的值对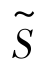 值的影响较大,所以考虑把非基变量x2换成基变量(称x2为入基变量).但是基变量只能有3个,必须从x3,x4,x5中换走一个作为非基变量(称为离基变量).至于换走哪一个,这需让入基变量x2保证所有的变量满足非负限制.为此,考虑让入基变量x2取正值,x1仍为非基变量取零.将方程组(7.3)等价变形为
值的影响较大,所以考虑把非基变量x2换成基变量(称x2为入基变量).但是基变量只能有3个,必须从x3,x4,x5中换走一个作为非基变量(称为离基变量).至于换走哪一个,这需让入基变量x2保证所有的变量满足非负限制.为此,考虑让入基变量x2取正值,x1仍为非基变量取零.将方程组(7.3)等价变形为
显然只有选择![]() ,才能使x3≥0,x4≥0,x5≥0同时成立.而当x2=3时,原基变量x5=3-3=0.因此确定x5为离基变量,得新基B1=(p2,p3,p4)和新基变量x2,x3,x4及非基变量x1,x5,此时对方程组(7.3)作初等变换,使新基变量x2,x3,x4的系数全变为1,得方程组的等价变形为:
,才能使x3≥0,x4≥0,x5≥0同时成立.而当x2=3时,原基变量x5=3-3=0.因此确定x5为离基变量,得新基B1=(p2,p3,p4)和新基变量x2,x3,x4及非基变量x1,x5,此时对方程组(7.3)作初等变换,使新基变量x2,x3,x4的系数全变为1,得方程组的等价变形为:
即
将式(7.6)代入目标函数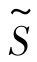 =-2x1-3x2中,得目标函数新的表达式为~S1=-9-2x1+3x5,于是得到线性规划问题(7.3)的一个等价形式,即
=-2x1-3x2中,得目标函数新的表达式为~S1=-9-2x1+3x5,于是得到线性规划问题(7.3)的一个等价形式,即
令x1=x5=0,得一基本可行解X(1)=(0,3,5,1,0)T,相应的目标函数值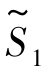 =-9-2×0+3×0=-9.显然这个解也不是最优解.因为目标函数
=-9-2×0+3×0=-9.显然这个解也不是最优解.因为目标函数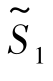 中x1的系数为负值,如果x1不取零而取正值,则目标函数值还可以减少.于是重复上述方法,将非基变量x1换作入基变量.为找出离基变量,在方程组(7.5)中令非基变量x5=0,得
中x1的系数为负值,如果x1不取零而取正值,则目标函数值还可以减少.于是重复上述方法,将非基变量x1换作入基变量.为找出离基变量,在方程组(7.5)中令非基变量x5=0,得
此时x2=3>0,为保证其他变量非负,令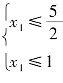 ,有
,有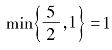 .显然只有选择x1=
.显然只有选择x1=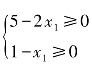 ,才能使x3≥0,x4≥0.而当x1=1时,有x4=1-1=0.因此选择x4为离基变量,得新基B2=(p1,p2,p3)和新基变量x1,x2,x3及非基变量x4,x5.将方程组(7.5)作等价变形,化为
,才能使x3≥0,x4≥0.而当x1=1时,有x4=1-1=0.因此选择x4为离基变量,得新基B2=(p1,p2,p3)和新基变量x1,x2,x3及非基变量x4,x5.将方程组(7.5)作等价变形,化为
即
将方程组(7.9)代入目标函数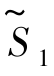 =-9-2x1+3x5中,得新目标函数
=-9-2x1+3x5中,得新目标函数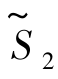 =-11+2x4-x5及原线性规划问题(7.3)的又一等价形式,即
=-11+2x4-x5及原线性规划问题(7.3)的又一等价形式,即
令x4=x5=0,得又一基本可行解X(2)=(1,3,3,0,0)T.
相应的目标函数值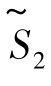 =-11+2×0-0=-11.它还不是最优解.因为目标函数值
=-11+2×0-0=-11.它还不是最优解.因为目标函数值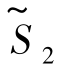 中非基变量x5的系数是负的,所以当x5取正值时,目标函数
中非基变量x5的系数是负的,所以当x5取正值时,目标函数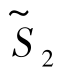 的值还有减小的可能.于是重复上述方法,将非基变量x5与基变量x3互换,得新基B3=(p1,p2,p5),新基变量x1,x2,x5,非基变量x3,x4及等价的方程组
的值还有减小的可能.于是重复上述方法,将非基变量x5与基变量x3互换,得新基B3=(p1,p2,p5),新基变量x1,x2,x5,非基变量x3,x4及等价的方程组
将其代入目标函数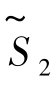 中,得相应的新目标函数
中,得相应的新目标函数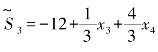 及相应的与(7.3)等价的线性规划问题:
及相应的与(7.3)等价的线性规划问题:
令x3=x4=0,又得一基本可行解X(3)(3,2,0,0,1)T,相应的目标函数值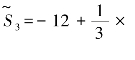
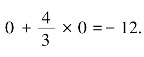 由于此时的目标函数
由于此时的目标函数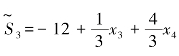 ,非基变量的系数均为正数,所以当它们之中任一个取正值时,都不能使目标函数S~3的值减少,因此X(3)=(3,2,0,0,1)T就是线性规划(7.12)使目标函数值最小的最优解.与它对应的基B3称为最优基.从而原线性规划问题(7.3)的最优解X=(x1,x2)=(3,2),相应的最优值max S=2×3+3×2=12.
,非基变量的系数均为正数,所以当它们之中任一个取正值时,都不能使目标函数S~3的值减少,因此X(3)=(3,2,0,0,1)T就是线性规划(7.12)使目标函数值最小的最优解.与它对应的基B3称为最优基.从而原线性规划问题(7.3)的最优解X=(x1,x2)=(3,2),相应的最优值max S=2×3+3×2=12.
通过此例可以发现,线性规划问题的单纯形法求解,就是不断重复换基,使基本可行解从其可行域的一个顶点转换到另一个顶点,使相应的目标函数值一次比一次更好,从而最终取得最优解.这就是单纯形法的基本思想.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




