齐次线性方程组解的讨论:大学应用数学

设有齐次线性方程组

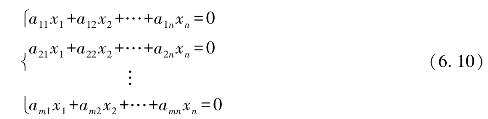
由于齐次线性方程组（6.10）的系数矩阵A与它的增广矩阵A～的秩总是相等，所以齐次线性方程组（6.10）总是有解，而且零解一定是它的解.于是由定理6.6可得如下定理.

定理6.7　齐次线性方程组（6.10）有非零解的充分必要条件是它的系数矩阵的秩小于它的未知量个数.

推论6.3　如果m=n，则齐次线性方程组（6.10）有非零解的充分必要条件是它的系数行列式等于零.

推论6.4　如果m＜n，则齐次线性方程组（6.10）必有非零解.

例6.26　设线性方程组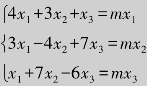有非零解，求m的值.

解　该方程组为齐次线性方程组，根据推论6.3知，该方程组有非零解的充分必要条件是它的系数行列式等于零，即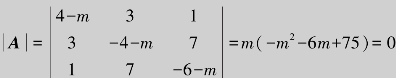.解得m=0或或

即当m=0或或时，原方程组有非零解.

例6.27　求解齐次线性方程组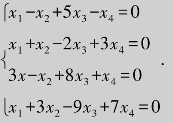

解　由于齐次线性方程组是一般线性方程组的特例，所以高斯-若尔当消元法对它仍然适用.

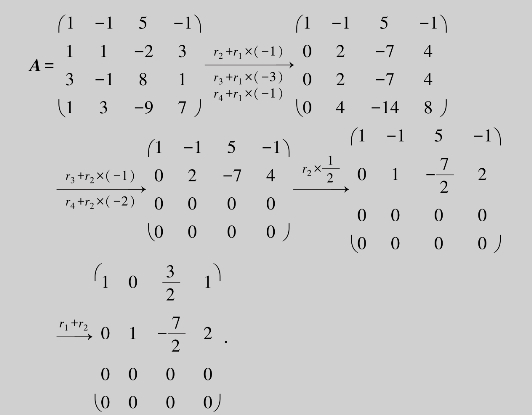
显然r（A）=2＜4（未知量个数），所以该方程组有无穷多解.设x3，x4为自由未知量，分别取任意常数C1，C2，于是得原方程组的解为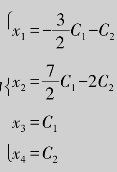（当C1=C2=0时，得零解）.

练习6.5

1.判断下列命题的正确性.

（1）（　　）线性方程组有解的充分必要条件是系数矩阵的秩与增广矩阵的秩相等.

（2）（　　）齐次线性方程组有非零解的充分必要条件是系数矩阵的秩小于未知量个数.

（3）（　　）齐次线性方程组的系数行列式不等于零，则它有解且只有零解.

（4）（　　）若=0，则矩阵方程AX=B无解.

2.讨论m取何值时，方程组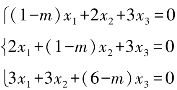有非零解.

3.求解下列线性方程组.

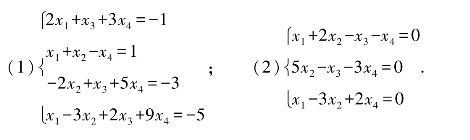
第6章　自测题

1.判断题

（1）（　　）若=0，则A=0.

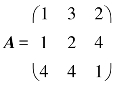（2）（　　）矩阵与矩阵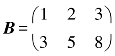不能左乘.

（3）（　　）线性方程组有解的充分必要条件是系数矩阵的秩与增广矩阵的秩相等.

（4）（　　）任意非零方阵都有逆矩阵.

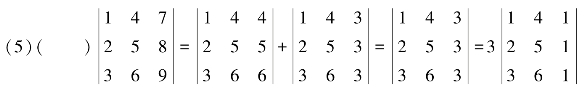
（6）（　　）齐次线性方程组有非零解的充分必要条件是系数矩阵的秩小于未知量个数.

2.选择题

（1）若AB=O，则________.

（A）A=O　　　　　　（B）B=O

（C）A=O或B=O　　　　（D）以上答案均不对

（2）若，则________.

（A）A=B　　　（B）AT=BT

（C）A-1=B-1　　（D）以上答案均不对

（3）设矩阵A2×2，B3×2，C3×3，下列可运算的式子是________.

（A）ABC　　　（B）BCA

（C）CBA　　　（D）BAC

（4）设A是可逆阵，下列运算正确的是________.(www.xing528.com)

（A）（2A）T=2AT　　（B）（2A）-1=2A-1

（C）[（（A）-1）-1]T≠[（（A）T）-1]-1　　　　（D）[（（A）T）T]-1=[（（A）-1）-1]T

（5）设A为n阶方阵，R（A）=r＜n，那么________.

（A）A可能不可逆　　　（B）

（C）A中所有r阶子式全不为零　　（D）A中没有不等于零的r阶子式

3.填空题

（1）

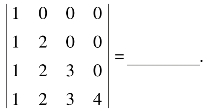
（2）A为三阶方阵，则

（3）设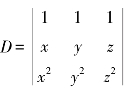，则元素x的代数余子式是________.

（4）用逆阵法解线性方程组AX=B的条件是________.

（5）若矩阵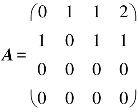，则R（A）=________.

4.解答题

（1）计算行列式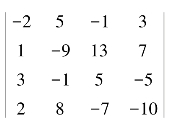的值.

（2）求矩阵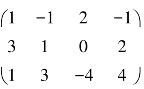的秩.

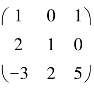（3）求矩阵的逆矩阵.

（4）讨论m取何值时，方程组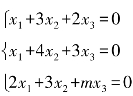有非零解?并求出它的一般解.

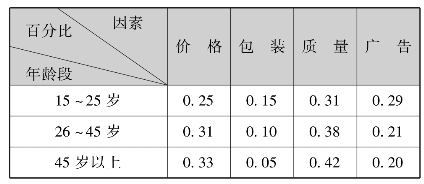
（5）通过市场调查，得到不同年龄的消费者在购买奶制品时优先考虑因素情况如表6.4所示，被调查者的年龄结构情况为：15～25岁占26%，26～45岁占47%，45岁以上占27%，求在消费者优先考虑的因素中，哪一个占的百分比最高?

表6.4

思政　阅读材料之六

数学之美

——图形王国

数学是一切科学的基础，它融入了我们生活中的方方面面，小小的字符与柔和的线条构成了大千世界的数学之美.

一个数学公式就是一个爱情密码.当年大数学家笛卡尔在给瑞典公主表白的时候，写了这样一封信，上面只有一句话，而这封信现在还供在欧洲的博物馆里，成为了千古佳话.那封信上写到：

r=a（1-sin θ）

各位，有谁知道它是什么意思吗?

r=a（1-sin θ）这个函数有两个变量，可对a赋值，然后进行求解.函数图像是心形线.这个方程又被称为“笛卡尔的爱情坐标公式”，如图所示，分别是a=1、a=2、a=3时的图像.

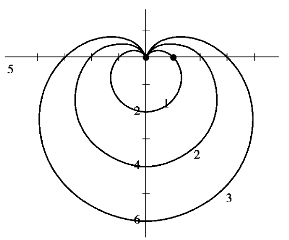
极简的公式，完整的循环，永恒的爱之密语

而这位公主呢，她恰好是个低调的数学迷，她一眼就看破了其中真意，于是优雅地在纸上，用直角坐标系将曲线画了出来，于是一个心形图案跃然纸上.

这就是数学的图形之美，她的美丽不像烟花般耀眼绚丽，却可给人带来心灵上的震撼.大家都会背李白的《登鹳雀楼》，下面让我们欣赏一下这首诗的图形之美吧！

白日依山尽

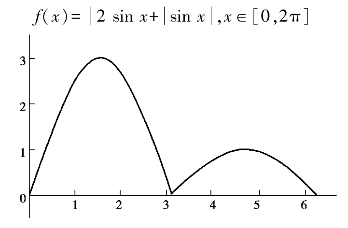
黄河入海流

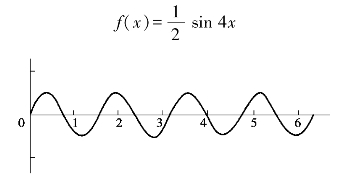
欲穷千里目

更上一层楼

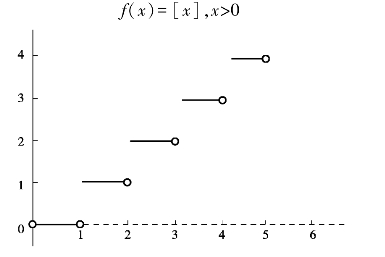
哪里有数学，哪里就有美，数学有诱人的魅力，数学有神奇的思想，数学更有巨大的力量.