一般线性方程组解讨论-大学应用数学

1.解的判定

设有线性方程组AX=B.

解线性方程组的一个基本方法是消元法.这一思想用矩阵反映出来，就是对方程组（6.6）的增广矩阵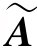施行行初等变换，最终将其化为行简化阶梯形矩阵

其中k≤n.

由于式（6.7）对应的线性方程组与原方程组是同解的，而且矩阵的初等变换不改变矩阵的秩，因此由式（6.7）不难得出以下结论：

（1）当dk+1≠0时，出现矛盾方程，故原方程组无解，此时r（A）=k，r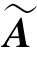（）=k+1，r（A）≠r （）；反之亦然.

（2）当dk+1=0时，有r（A）=r（A～）.

①若k=n，式（6.7）即为

此时得方程组唯一解x1=d1，x2=d2，…，xn=dn.

②若k＜n，式（6.7）对应的线性方程组为

这里有n-k个自由未知量xk+1，xk+2，…，xn，它们可以任意取值，所以此时原方程组有无穷多个解：

其中C1，C2，…，Cn-k为任意常数.

综上所述，得到线性方程组（6.6）解的判定定理.(www.xing528.com)

定理6.5　线性方程组（6.6）有解的充分必要条件是它的系数矩阵A的秩与它的增广矩阵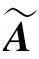的秩相等，即r（A）=r（）.

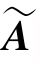定理6.6　设线性方程组（6.6）满足r（A）=r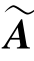（）=k.

（1）若k=n（未知量个数），则线性方程组（6.6）有唯一解.

（2）若k＜n（未知量个数），则线性方程组（6.6）有无穷多解.

例6.23　设线性方程组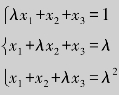.问：λ取何值时，方程组无解?有解?有无穷解?有唯一解?

显然，当λ=-2时，r（A）=2，r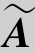（）=3，r（A）≠r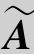（），此时方程组无解.

当λ≠-2时，对矩阵B施行行初等变换如下：

由矩阵C知，当λ=1时，r（A）=r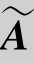（）=1＜3（未知量个数），方程组有解，且有无穷多组解；当λ≠-2且λ≠1时，r（A）=r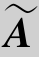（）=3（未知量个数），方程组有解，且有唯一解.

2.用高斯-若尔当消元法求解线性方程组

求解线性方程组有很多方法，其中一种方法是高斯-若尔当消元法.正如前面讨论的那样，对一般线性方程组（6.6）的增广矩阵施行有限次的行初等变换后，得到行简化阶梯形矩阵，由此便可以确定线性方程组（6.6）有解、无解及解的表达式.这种通过对方程组的增广矩阵施行行初等变换来求解方程组的方法称为高斯-若尔当消元法.它的优点在于既可判断出方程组解的存在性，又能同时把解求出来.

这里r（A）=r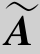（）=2＜4（未知量个数），所以方程组有无穷多解，且x3，x4为自由未知量，设它们分别取任意常数c1，c2，得方程组的无穷多解为：