奇偶函数的傅里叶级数应用

若f（x）的周期为T=2l，则.

（1）当f（x）为奇函数时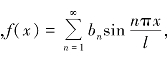其中

（2）当f（x）为偶函数时，其中

这个结论说明，如果f（x）为奇函数，那么它的傅里叶级数是只含有正弦项的正弦级数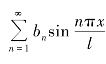；如果f（x）为偶函数，那么它的傅里叶级数是只含有余弦项的余弦级数

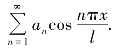
例5.24　设f（x）是周期为2π的周期函数，它在[-π，π]上的表达式为f（x）=x.将f（x）展开成傅里叶级数.

解　首先，所给函数满足收敛定理的条件，在点x=（2k+1）π　（k=0，±1，±2，…）处不连续，因此f（x）的傅里叶级数在点x=（2k+1）π　（k=0，±1，±2，…）处收敛于

在连续点x≠（2k+1）π　（k=0，±1，±2，…）处收敛于f（x）.

其次，若不计x=（2k+1）π　（k=0，±1，±2，…），则f（x）是周期为2π的奇函数.

按照公式有an=0（n=0，1，2，…）而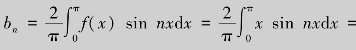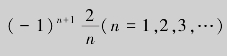，将求得的bn代入正弦级数，得f（x）的博里叶级数展开式为

例5.25　将周期函数（E为正的常数）展开成傅里叶级数.

解　所给函数满足收敛定理的条件，它在整个数轴上连续，因此u（t）的傅里叶级数处处收敛于u（t）.

因为u（t）是周期为2π的偶函数，所以有bn=0，而

将求得的an代入余弦级数，得u（t）的傅里叶级数展开式为

练习5.4 1.填空题.

（1）设f（x）是周期为2π的周期函数，在[-π.π]上的表达式为f（x）=x+1，又设S（x）为f（x）的傅里叶级数的和函数，则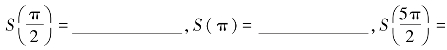____________，S（3π）=____________.

（2）设f（x）=1+x，0≤x≤π，则将f（x）展开成正弦级数，有an=________________；又若将f（x）展开成余弦级数，有bn=____________.

2.将下列周期为2π的函数展开成傅里叶级数，其中f（x）在[-π，π）上的表达式为

3.将下列各周期函数展开成傅里叶级数，其中f（x）在一个周期内的表达式为

第5章自测题

1.判断题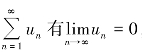

（1）（　　）若级数，则此级数收敛.

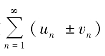（2）（　　）若级数收敛，级数发散，则级数发散.

（3）（　　）若级数收敛，则

（4）（　　）若加括号后所形成的级数收敛，则去掉括号后级数仍收敛.

（5）（　　）若级数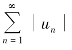收敛，则级数必收敛.

2.选择题

（1）下列级数收敛的是____________.

（2）级数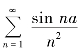的收敛性____________.

（A）条件收敛　　（B）绝对收敛　　　（C）发散　　　（D）不确定

（3）级数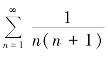的和是____________.(www.xing528.com)

（A）1　　　（B）2　　　（C）+∞　　　（D）0

（4）在下列级数中，发散的级数是____________.

（5）幂级数在开区间（-1，1）内的和函数是____________.

3.填空题

（1）函数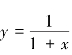在区间内幂级数展开式为____________

.

（2）两正项级数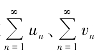满足un≤vn（n=1，2，3…），若级数______，则级数必定____________；若级数，则级数必定____________.

（3）若级数绝对收敛，则级数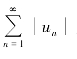必定____________；若级数条件收敛，则级数必定____________.

（4）级数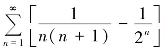的和为____________.

（5）若交错级数满足：①un≥un+1；②.则级数敛散性为____________，并且其和S≤____________.

4.解答题

（1）判断下列级数的收敛性.

（2）求下列级数的收敛区间.

（3）求级数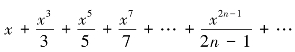在收敛域内的和函数.

（4）将函数f（x）=cos x展开成关于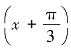的幂级数.

（5）将函数展开成关于（x-2）的幂级数，并指出其收敛域

思政　阅读材料之五

数学奖大满贯华人数学家还有谁……

丘成桐：美国现代数学家，菲尔兹和沃尔夫奖得主.原籍广东蕉岭，1949年4月4日生于广东汕头，后全家移居中国香港.早年丧父，家境清贫，母亲克服种种困难供其上学.在香港培正中学就读时勤奋钻研数学，成绩优异.1966年入香港中文大学数学系，1969年提前修完四年课程，为美国伯克利加州大学陈省身教授所器重，破格录取为研究生.在陈省身指导下，1971年获博士学位.1983年，他被授予菲尔兹（Fields）奖章——这是世界数学界的最高荣誉.后在斯托尼布鲁克的纽约州立大学、斯坦福大学等校任教，并为普林斯顿高级研究所终身教授，曾于圣地亚哥加州大学任教，现任教于哈佛大学.

19岁的时候来到美国伯克利.“21岁毕业时就注定要改变数学的面貌”这不是作者的话，这是几年前加州大学洛杉矶分校希望把丘教授聘请过来的时候，系里讨论时一个年纪很大的几何学家引用陈省身先生说的一句话.在伯克利学习期间他证明了卡拉比猜想、正质量猜想，开创了一个崭新的领域：几何分析.当年他只有28岁.也就是说，从入学伯克利到他在世界数学家大会做一小时报告之间相隔还不到10年.在他作报告的那一年，陈景润先生也同时被邀请做45分钟的报告.

20世纪70年代左右的伯克利分校是世界微分几何的中心，云集了许多优秀的几何学家和年轻学者.在这里，丘成桐得到IBM奖学金，并师从著名微分几何学家陈省身.数学是奇妙的，也是生涩的.即使是立志在数学领域建功立业的年轻学生，能坚持到最后并出成果的，也是寥若晨星.丘成桐正可谓这样一颗“晨星”.常常有这样的情景——偌大的教室中，听课的学生越来越少，最后竟然只剩下教授一人面对讲台下唯一的学生悉心教诲.这唯一的学生，就是丘成桐.到伯克利分校学习一年后，丘成桐便完成了他的博士论文，文中巧妙地解决了当时十分著名的“沃尔夫猜测”.他对这个问题的巧妙解决，使当时的世界数学界意识到一个数学新星的出现.

1976年，丘成桐被提升为斯坦福大学数学教授.

1978年，他应邀在芬兰举行的世界数学大会上做题为《微分几何中偏微分方程作用》的学术报告.这一报告代表了20世纪80年代前后微分几何的研究方向、方法及其主流.这之后，他又解决了“正质量猜测”等一系列数学领域难题.

丘成桐的研究工作深刻又广泛，涉及微分几何的各个方面，成果累累.

1981年，他32岁时，获得了美国数学会的维布伦（Veblen）奖——这是世界微分几何界的最高奖项之一.

1982年，他被授予菲尔兹（Fields）奖章——这是世界数学界的最高荣誉.

1989年，美国数学会在洛杉矶举行微分几何大会，丘成桐作为世界微分几何的新一代领导人出任大会主席.命运是公平的，奖章、荣誉，授予了那个在教室中坚持到最后的人.但这并不会让丘成桐止步不前，他继续进行着大量繁杂的研究工作，并不断取得成就.坚韧、坚持、锲而不舍，这就是丘成桐的精神.著名数学家郑绍远先生回忆说，对于许多艰深的数学问题，丘成桐已思考近20年，虽然仍未解决，他还是没有轻易放弃思考.

1994年，他又荣获了克劳福（Crawford）奖.大学期间，他以三年时间修完全部必修课程，还阅读了大量课外资料.他的突出成绩和钻研精神为当时的美籍教授萨拉夫所赏识，萨拉夫力荐他到美国加利福尼亚大学伯克利分校攻读博士研究生.

2010，获得沃尔夫数学奖，这是在阿贝尔奖出现前最接近诺贝尔奖的奖项，是数学界的终身成就奖.