大学应用数学幂级树近似计算简单应用

例5.20　求e的近似值，要求误差不超过0.0001.

解　根据ex的麦克劳林展开式：

于是令x=1得，

由于要求|rn|＜0.000 1，凭观察和试算，当取n=8时，

故取n=8，计算近似值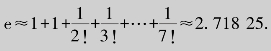

例5.21　计算积分的近似值，准确到第四位小数.

解　由于，因此所给积分不是广义积分.如果定义被积函数在x=0处的值为1，则它在积分区间[0，1]上连续.的麦克劳林级数是

故

这是一个交错级数，由于第四项，因此取前三项来计算积分的近似值，可准确到第四位小数，于是，

练习5.3

1.填空题.

（1）f（x）=ex的麦克劳林级数为________________，其中x∈____________.

（2）f（x）=ln（1+x）的麦克劳林级数为____________，其中x∈____________.(www.xing528.com)

（3）f（x）=sin 2x的麦克劳林级数为______________，其中x∈_____________.

（4）f（x）=的麦克劳林级数为______________，其中x∈____________.

（5）f（x）=的麦克劳林级数为______________，其中x∈____________.

（6）f（x）=cos x的麦克劳林级数为______________，其中x∈____________.

2.将下列函数展开成x的幂级数，并写出展开式成立的区间.

（1）　　　　（2）ax；

（3）sin2x；　　　（4）（1+x）ln（1+x）.

3.将函数展开成x的幂级数.

4.利用函数的幂级数展开式求下列各数的近似值.

（1）ln 3（误差不超过0.000 1）　　　（2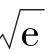）（误差不超过0.001）.

5.利用被积函数的幂级数展开式求下列定积分的近似值.