【摘要】:由上述定理,可以将具有任意阶导数的函数展开成x的幂级数,具体展开法较常用的有以下两种:1.直接展开法求f的各阶导数.求f(n=1,2,…).写出幂级数,并求出R.考察余项Rn是否趋于零.如果趋于零,则f在内的幂级数展开式为这里的余项.例5.16将函数f=ex展开成x的幂级数.解f=f′=f″=…
由上述定理,可以将具有任意阶导数的函数展开成x的幂级数,具体展开法较常用的有以下两种:
1.直接展开法
(1)求f(x)的各阶导数.
(2)求f(n)(0)(n=1,2,…).
(3)写出幂级数 ,并求出R.
,并求出R.
(4)考察余项Rn(x)是否趋于零.如果趋于零,则f(x)在(-R,R)内的幂级数展开式为
这里的余项![]() (ξ在0与x之间).
(ξ在0与x之间).
例5.16 将函数f(x)=ex展开成x的幂级数.
解 f(x)=f′(x)=f″(x)=…=f(n)(x)=…=ex,有
f(0)=f′(0)=f″(0)=…=f(n)(0)=…=1,于是得到ex的麦克劳林级数
此级数的收敛半径为R=+∞.
又因为
由于e|x|有界,而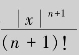 为收敛级数
为收敛级数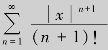 的一般项,所以有
的一般项,所以有 0.因而
0.因而![]() ,于是麦克劳林级数收敛于ex,即(https://www.xing528.com)
,于是麦克劳林级数收敛于ex,即(https://www.xing528.com)
同理,可以求得
2.间接展开法
利用幂级数可以逐项求导、逐项积分及已知函数的幂级数展开式将函数展开成幂级数.
例5.17 将函数f(x)=ln(1+x)展开成x的幂级数.
解 因为![]() 是收敛的等比级数
是收敛的等比级数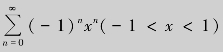 的和函数
的和函数
所以将上式从0到x逐项积分,得
例5.18 将函数f(x)=cos x展开成x的幂极数.
必须熟记如下五个函数的幂级数展开式:
ex,sin x,cos x,ln(1+x),(1+x)m
例5.19 将函数![]() 展开成x的幂级数.
展开成x的幂级数.
解 将函数变形为 ;由于
;由于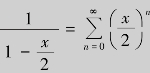 ,所以
,所以
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




