1.幂级数的定义
定义5.3 把形如![]() 的级数称为(x-x0)的幂级数,其中a0,a1,a2,…,an,…称为幂级数的系数.当x0=0时,级数变为
的级数称为(x-x0)的幂级数,其中a0,a1,a2,…,an,…称为幂级数的系数.当x0=0时,级数变为![]() ,把这种类型的级数称为x的幂级数.
,把这种类型的级数称为x的幂级数.
例如, 都是x的幂级数.
都是x的幂级数.
2.幂级数的收敛域
对于x的幂级数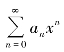 ,要求其收敛点,我们先找出使该级数绝对收敛的点,即使
,要求其收敛点,我们先找出使该级数绝对收敛的点,即使 收敛的点,然后由正项级数的比值审敛法求幂级数收敛的条件.由
收敛的点,然后由正项级数的比值审敛法求幂级数收敛的条件.由 ,得:当
,得:当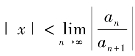 时,级数
时,级数 收敛,此时的收敛点在某个领域内,领域半径称为收敛半径;当
收敛,此时的收敛点在某个领域内,领域半径称为收敛半径;当 时,级数
时,级数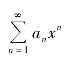 发散;当
发散;当 时,级数
时,级数 的收敛性需另作判断.
的收敛性需另作判断.
定理5.6 对于x的幂级数 ,如果
,如果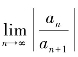 存在(或为无穷大),则该幂级数的收敛半径为
存在(或为无穷大),则该幂级数的收敛半径为
例5.10 求幂级数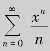 的收敛域.
的收敛域.
当x=1时,级数成为![]() ,它是发散的;当x=-1时,级数成为
,它是发散的;当x=-1时,级数成为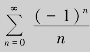 ,它是收敛的.
,它是收敛的.
所以,级数![]() 的收敛域为[-1,1).
的收敛域为[-1,1).
例5.11 求幂级数 的收敛域.
的收敛域.
解  ,所以,级数
,所以,级数 的收敛域为(-∞,+∞).
的收敛域为(-∞,+∞).
例5.12 求幂级数 的收敛半径.(https://www.xing528.com)
的收敛半径.(https://www.xing528.com)
解 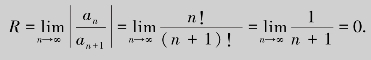 所以,幂级数
所以,幂级数 仅在点x=0处收敛.
仅在点x=0处收敛.
例5.13 求幂级数 的收敛域.
的收敛域.
分析 该级数中只出现x的偶次幂,不能直接用定理来求收敛半径R.可考虑比值审敛法.
解 设![]() ,于是
,于是
当![]() ,即|x|<
,即|x|<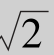 时,幂级数绝对收敛,收敛半径为
时,幂级数绝对收敛,收敛半径为 ;当
;当![]() ,即|x|>
,即|x|> ,幂级数发散;当x=
,幂级数发散;当x=![]() 时,级数成为
时,级数成为 ,它是发散的.
,它是发散的.
所以,幂级数 的收敛域是(-2,2).
的收敛域是(-2,2).
对于(x-x0)的幂级数的收敛域求法与上述方法类似,也可以用变量代换令x-x0=t,从而代换成t的幂级数求收敛区域.
例5.14 求幂级数 的收敛域.
的收敛域.
解 令t=x-1,上述级数变为 ,因为
,因为
当t=2时,级数成为 ,此级数发散;当t=-2时,级数成为
,此级数发散;当t=-2时,级数成为 ,此级数收敛.因此,级数
,此级数收敛.因此,级数 的收敛域为-2≤t<2.此时-2≤x-1<2,即-1≤x<3.
的收敛域为-2≤t<2.此时-2≤x-1<2,即-1≤x<3.
所以,级数 的收敛域为[-1,3).
的收敛域为[-1,3).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




