【摘要】：任意项级数的各项都换为它的绝对值，那么对应一个正项级数，该正项级数与原级数的收敛性有如下关系.定理5.5若收敛，则绝对收敛；如果发散而收敛，则称条件收敛.例如，级数绝对收敛；级数条件收敛.例5.8判定级数的收敛性，若收敛，则指出是绝对收敛还是条件收敛.解因为，所以，级数绝对收敛.例5.9判别级数的收敛性.解因为而级数是收敛的，根据比较审敛法可知，级数也收敛，所以，级数绝对收敛.练习5.1
任意项级数的各项都换为它的绝对值，那么对应一个正项级数，该正项级数与原级数的收敛性有如下关系.
定理5.5 若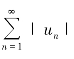
收敛，则
绝对收敛；如果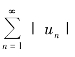
发散而
收敛，则称
条件收敛.
例如，级数
绝对收敛；级数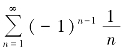
条件收敛.
例5.8 判定级数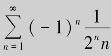
的收敛性，若收敛，则指出是绝对收敛还是条件收敛.
解 因为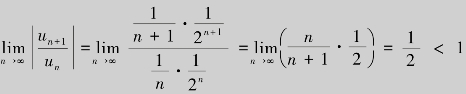
，所以，级数
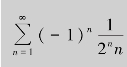绝对收敛.
例5.9 判别级数
的收敛性.
解 因为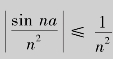
而级数
是收敛的，根据比较审敛法可知，级数
也收敛，所以，级数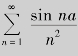
绝对收敛.
练习5.1
1.填空题.
（1）级数
的部分和Sn ____________，此级数的和S=____________.
（2）当|x|＜1时，级数
的和S=____________.(www.xing528.com)
（3）已知级数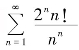
收敛，则
2.选择题.
（1）下列说法正确的是____________.
（2）下列级数发散的是____________.
（3）下列级数条件收敛的是____________.
3.判别下列级数的收敛性，如果收敛，求其和.
4.判别下列级数的收敛性.
5.用比较法判别下列级数的收敛性.
6.用比值法判别下列级数的收敛性.
7.判别下列级数的收敛性；如果是收敛的，指出是绝对收敛还是条件收敛.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
