1.级数的定义
对于数列{un},我们把和式u1+u2+u3…+un…称为常数项无穷级数,简称级数,记作![]() ,其中un称为级数的一般项.
,其中un称为级数的一般项.
例如, 等都是常数项级数.
等都是常数项级数.
在上述和式中,如果仅取有限项,即项数n分别为1,2,3,…,n,则对应的和式分别为:u1=S1,u1+u2=S2,u1+u2+u3=S3,…,u1+u2+u3+…+un=Sn,这里,我们把级数![]() 中的部分项的和式u1+u2+u3+…+un=Sn叫级数的部分和,把级数中部分和余下的部分叫级数的余项,记作Rn,有
中的部分项的和式u1+u2+u3+…+un=Sn叫级数的部分和,把级数中部分和余下的部分叫级数的余项,记作Rn,有![]() 把数列S1,S2,S3,…,Sn,…称为部分和数列{Sn}.
把数列S1,S2,S3,…,Sn,…称为部分和数列{Sn}.
2.级数收敛与发散的定义
定义5.1 如果级数![]() 的部分和数列{Sn}有极限S,即
的部分和数列{Sn}有极限S,即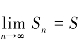 ,则称级数
,则称级数![]() 收敛,这时极限S称为级数的和,记作
收敛,这时极限S称为级数的和,记作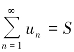 ;如果{Sn}无极限,则称级数
;如果{Sn}无极限,则称级数![]() 发散.
发散.
例5.1 证明等比级数(或几何级数)
当|q|<1时收敛,当|q|≥1时发散.
证 如果q≠1,其前n项的和
当|q|<1时,由于![]() ,于是
,于是![]() ,即等比级数收敛,且其和为
,即等比级数收敛,且其和为![]()
当|q|>1时,由于![]() ,于是当n→∞时,Sn是无穷大量,因此级数发散.
,于是当n→∞时,Sn是无穷大量,因此级数发散.
当q=1时,级数变为a+a+a+…,于是![]() ,因此级数发散.
,因此级数发散.
当q=-1时,级数变为a-a+a-a+…;当n为奇数时,Sn=a,而当n为偶数时,Sn=0;即当n→∞时.Sn无极限,所以级数发散.
综上所述,几何级数![]() 当|q|<1时收敛,当|q|≥1时发散.
当|q|<1时收敛,当|q|≥1时发散.
例5.2 证明级数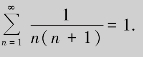
当n→∞时,Sn→1.
根据级数收敛的定义可知,级数的收敛性、部分和的极限与余项之间有如下关系:级数
例5.3 证明调和级数![]() 发散.(https://www.xing528.com)
发散.(https://www.xing528.com)
分析 由级数收敛的定义可如,当级数的部分和余项的极限不为零时,该级数就发散,我们只需证明其部分和的余项的极限非零即可.
证 当i=1,2,3,…,n时,![]() ,于是有
,于是有
显然,余项Rn不是无穷小量.因此,级数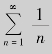 发散.
发散.
3.数项级数收敛的必要条件
定理5.1 若级数![]() 收敛,则
收敛,则![]()
推论5.1 对于级数![]() ,当n→∞时,若un不趋于零,则此级数必发散.
,当n→∞时,若un不趋于零,则此级数必发散.
例如,因为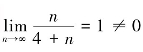 ,所以级数
,所以级数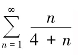 发散.
发散.
必须注意的是:级数的一般项趋于零并不是级数收敛的充分条件.
有些级数虽然一般项趋于零,但仍然是发散的.如例5.3已证明调和级数![]() 发散.
发散.
4.数项级数的基本性质
由级数收敛性定义.可得如下性质:
性质5.1 若级数![]() 收敛,其和为S,又k为常数。则
收敛,其和为S,又k为常数。则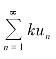 也收敛,且
也收敛,且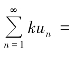
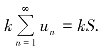
性质5.2 若两级数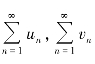 收敛,且
收敛,且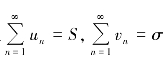 ,则两级数的代数和也收敛,且
,则两级数的代数和也收敛,且
性质5.3 在级数中去掉、加上或改变有限项,不会改变级数的收敛性.
性质5.4 收敛级数中的各项任意合并(即加上括号)后形成的新级数仍然收敛,而且其和不变.
但是,如果加括号后所形成的级数收敛,则不能断定原来的级数也收敛.例如,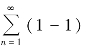 是收敛的,但级数1-1+1-1+1-1+…发散.
是收敛的,但级数1-1+1-1+1-1+…发散.
推论5.2 一个级数如果添加括号后所成的新级数发散,那么原级数一定发散.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




