《大学应用数学》二重积分的计算方法

通过对二重积分概念的建立，将一些非均匀变化所对应的量归结为二重积分问题.但是，若仅仅依赖于二重积分的定义或几何意义来求解二重积分，并不是一种切实可行的办法.事实上我们可以借助于一元函数定积分来帮助解决二重积分的计算问题.为便于问题的直观分析，我们考察：当被积函数f（x，y）≥0时，二重积分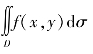的计算.

1.直角坐标系下二重积分的计算

设曲顶柱体的底是有界闭区域D，其中D是由直线x=a，x=b和曲线y=φ1（x），y=φ2（x）所围成的区域（图4.16），即D：a≤x≤b，φ1（x）≤y≤φ2（x）；曲顶柱体的曲顶面所对应的方程为z=f（x，y）.

图4.16

可以采取定积分中的元素法来计算该曲顶柱体的体积，如图4.17所示.

（1）先计算截面面积.在闭区间[a，b]上点x0处用垂直于坐标轴Ox的平面x=x0去截该曲顶柱体，可以得到一个截面，该截面是一个以闭区间[φ1（x），φ2（x）]为底，曲线z=f（x0，y）为曲边的曲边梯形（见图4.17的阴影部分），故该截面的面积为于是对于闭区间[a，b]上的任意点x处的裁面面积为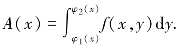

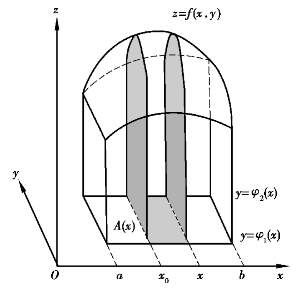
图4.17

（2）再计算体积元素.对于闭区间[a，b]上的任意点x，考察[x，x+dx]上的体积元素（体积的近似值），得dV=A（x）dx.

（3）后求体积（体积元素的积分）.

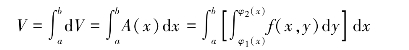
此积分顺序是，先求积分，得到一个关于x的变量式，再将该变量式在区间[a，b]上对x求积分.即将该问题转化为两次求积分，也称为二次积分或累次积分.

由二重积分的定义，曲顶柱体的体积V可以表示为底部区域上曲顶函数的二重积分，即

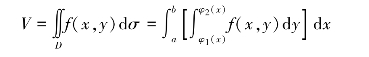
或

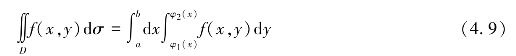
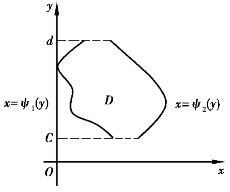
图4.18

由此可见：二重积分可以转化为累次积分.事实上，以上分析二重积分的计算方法对于被积函数在f（x，y）≤0时同样成立.

必须注意的是：在求积分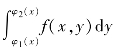的过程中，应将x当作常量.

这里，我们所分析的曲顶柱体的积分区域中，自变量x在常量之间变化，而自变量y在变量之间变化，我们所采取的措施是先对y、后对x求二次积分；若自变量y在常量c和d之间变化，而另一个自变量x在变量ψ1（y）和ψ2（y）之间变化时，则积分区域为D：ψ1（y）≤x≤ψ（y），c≤y≤d，如图4.18所示，则有

因此，将二重积分转化为二次积分有两种形式，而具体选择哪一种形式的二次积分，关键是要考虑积分区域和被积函数的特点.

例4.30　计算二重积分，其中积分区域D是由直线y=1、x=2、y=x所围成.

解　由于积分区域为（图4.19）D：1≤x≤2，1≤y≤x，因此可用（4.9）先对y、后对x求二次积分，即

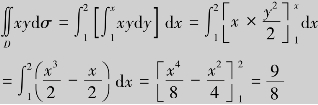
也可以考虑为D：1≤y≤2，y≤x≤2（图4.20）.因此先对x、后对求x二次积分，即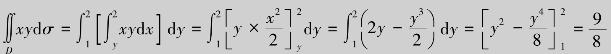

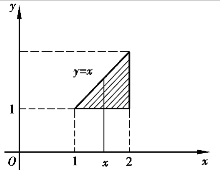
图4.19　

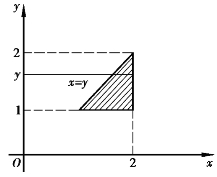
图4.20

例4.31　计算二重积分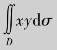，其中积分区域D是由抛物线y2=x及直线y=x-2所围成.

解　积分区域如图4.21所示，若先对x、后对y求二次积分，则积分区域为D：-1≤y≤2，y2≤x≤y+2，于是

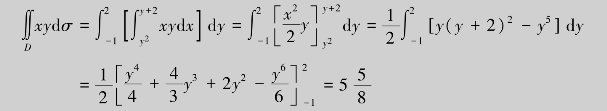
若先对y、后对x求二次积分，则当0≤x≤4时，φ1（x）≤y≤φ2（x），其中φ1（x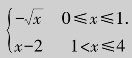）=，φ2（x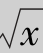）=，则必须将区域D分割为D1和D2两部分，如图4.22所示，其中

因此根据二重积分的性质4.6，就有

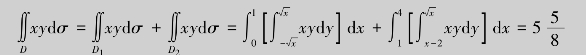
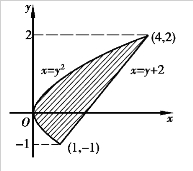
图4.21　

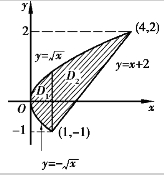
图4.22

例4.32　设积分区域是由直线y=x与曲线y=x2所围成，将二重积分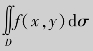表示为两种不同次序的二次积分.

解　积分区域如图4.23所示.若先对y求积分，则积分区域可表示为D：0≤x≤1，x2≤y≤x，积分为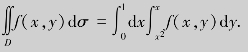

若先对x求积分，则积分区域可表示为0≤y≤1，y≤x≤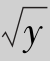，如图4.24所示，其积分为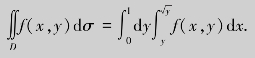

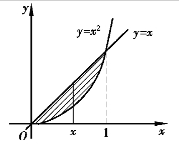
图4.23

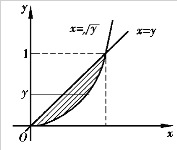
图4.24

例4.33　计算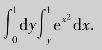

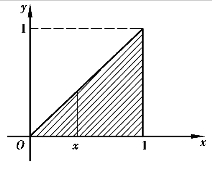
图4.25

分析　如果先对x求积分，则被积函数ex2的原函数不易求出.在这种情况下，可以考察先对y求积分，即交换积分次序.

解　首先将积分区域用点集表示，即0≤y≤1，y≤x≤1，对应的区域如图4.25所示.

再将图中的积分区域改写成自变量的另一种条件关系，即x在常量之间，0≤x≤1，此时，0≤y≤x.

最后交换积分次序并求出该区域上的二次积分：

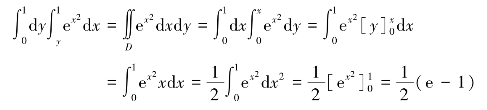
对于有些积分区域而言，在直角坐标系下表达式比较复杂，而该区域在极坐标系下的表达式相对简单，我们可以把直角坐标系下的二重积分转化为极坐标系下的二重积分.

2.极坐标系下二重积分的计算

将直角坐标系下的二重积分转化为极坐标系下的二重积分，需要将被积表达式代换成极坐标系下的被积表达式.关键是要将直角坐标系下的面积元素代换成极坐标系下的面积元素（见图4.26中的阴影部分），即dxdy=dσ=ρdρdθ.被积函数式代换法为x=>ρ cos θ，y=ρ sin θ.

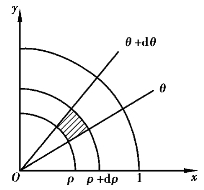
图4.26

例4.34　求，其中积分区域D为单位圆在第一象限内的部分.

分析　如果被积函数直接对x或直接对y求职分，都不易求出原函数，因此可将其转化为极坐标系下的积分.

解　（1）将直角坐标系下的被积表达式转化为极坐标系下的被积表达式，即

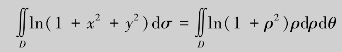
（2）确定积分变量ρ，θ的范围，有

（3）将极坐标系下的二重积分转化为二次积分

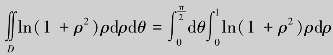
（4）求二次积分得

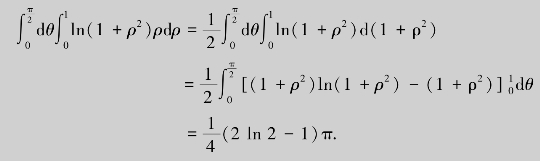
例4.35　计算二重积分，其中积分区域D是由圆x2+y2=2x所围成的.

解　在极坐标系下，积分区域D（见图4.27）可以表示为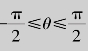：，0≤ρ≤2 cos θ.于是

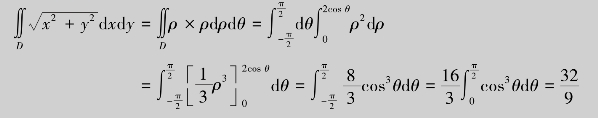
例4.36　计算二重积分，其中D：x2+y2≤R2.

分析　由于被积函数的积分不能直接求出，因此，将其转化为极坐标系下的二重积分.

解　由图4.28可知，区域D1在极坐标系下的条件为：0≤θ≤，0≤ρ≤R，于是

特别地，当R→+∞时，积分区域为整个xOy平面，有

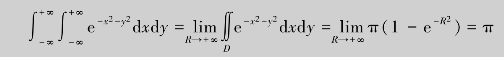(www.xing528.com)

而

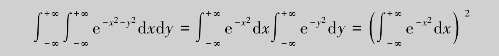
于是有

一般情况下，如果积分区域与圆有关系，或被积函数为f（x2+y2）的形式，则使用极坐标系下的积分法比较简便.

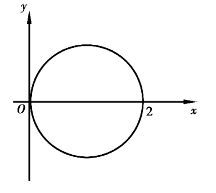
图4.27

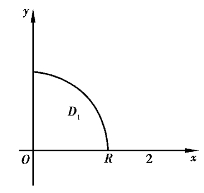
图4.28

练习4.5

1.填空题

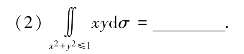
（3）设D：0≤x≤2，0≤y≤3，则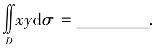

（4）设区域D由y=x，xy=1，x=2围成，则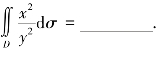

2.选择题

（1）设D是由单位圆在第二象限内的部分组成，则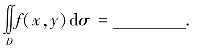

（2）D是矩形闭区域：|x|≤1，|y|≤1，则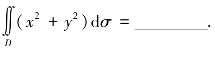

（3）设区域D由直线y=x，x=1和y=0围成，则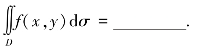

（4）设D={（x，y）|x2+y2≤a2，a＞0，y≥0}，在极坐标系下，二重积分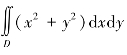可以表示为________.

3.计算下列二重积分.

（1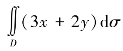），D是由两坐标轴及直线x+y=2所围成的闭区域.

（2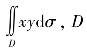）是由抛物线y2=2x及直线y=x-4所围成的闭区域.

（3），其中D由y=x，y2=x所围成的闭区域.

（4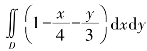），其中D由x=2，x=-2，y=1，y=-1围成的闭区域.

（5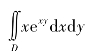），其中D由x=1，x=2，y=0及围成的闭区域.

（6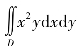），其中D由x2+y2≤1在第一象限内的部分.

（7），其中D：π2≤x2+y2≤4π2.

4.计算

第4章　自测题

1.填空题

（1）函数的定义域为________.

（2）二重极限

（3）如果函数f（x+y，x-y）=x2+y2，则函数f（x，y）=________.

（4）二重积分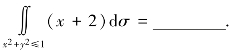

（5）函数z=4（x-y）-x2-y2的驻点为________.

2.选择题

（1）关于二元函数可微与可导的关系，下列叙述正确的是________.

（A）可微的点偏导数一定存在　　　（B）偏导数存在的点一定可微

（C）可微是偏导数存在的充要条件　　（D）都不能确定

（2）函数z=y cos x在点P（0，1）处的全微分为________.

（A）cos ldy+dx　　　（B）dy

（C）sin ldy+cos ldx　　　（D）sin ldy+sin ldx

（3）闭区域上连续函数的最值________.

（A）一定存在　　　（B）不一定存在

（C）一定在驻点处取得　　　（D）一定在边界线上取得

（4）设区域D由直线y=x，x=1和y=0围成，则

（5）设积分区域D为：x2+y2≤2y，则

3.计算题

（1）求下列函数的偏导数

（2）求函数z=x2-xy+y2+9x-6y+20的极值，

（3）某工厂要生产甲、乙两种产品，两种产品的单价分别是200元与150元，若成本函数为C（x，y）=2x2+y2，x，y分别为甲、乙两种产品的产量.问应如何安排产量可以使工厂的利润最大.

（4）设平面薄片所占的区域D是由抛物线y=x2及直线y=x所围成，在任意点（x，y）处的面密度为f（x，y）=x2y，求该薄片的质量.

（5）求二次积分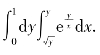

思政　阅读材料之四

华罗庚的人生故事

华罗庚一生都奉献给了中国数学，他先后开创了中国解析数论、矩阵几何学型群、自安函数论等，被誉为“中国现代数学之父”“人民科学家”.华罗庚虽仅有初中学历，但其一生发表数学研究论文200余篇，专著和科普性著作数十种，被芝加哥大学列入“当今世界88位数学伟人”之一.

一、爱琢磨数学，自学成英才

华罗庚（1910—1985年）出生在江苏省常州市金坛县（现为县级市）一个贫困家庭.这是当时一个非常闭塞的县城.童年时代，华罗庚特别爱动脑，对于一些别人看来司空见惯的事，往往也表现出浓厚的兴趣，常提出一些似乎希奇的问题.有一次，他同别人一块去城郊玩耍，见一座荒坟旁有石人、石马，就问比他大的同伴：“这些石人、石马有多重?”同伴回答说：“这怎么能知道呢.”华罗庚却不甘心，沉思片刻，说：“以后总会有方法知道的.”

华罗庚的数学作业经常有涂改的痕迹，很不整洁，老师开始时非常不满意.后来经过仔细辨别，老师发现华罗庚是在不断改进和简化自己的解题方法.华罗庚在中学读书时，曾对传统的珠算方法进行了认真思考.他经过分析认为，珠算的加减法难以再简化，但乘法还可以简化.凭着这一点改进，再加上他擅长心算，华罗庚在当时上海的珠算比赛中获得了冠军.

初中毕业后，华罗庚在上海上了一年职业学校，后因交不起学费，辍学回家帮父亲料理小杂货店.华罗庚没有屈从于命运的安排，毅然开始自学生涯.他每天坚持自学10个小时以上，没有纸，就用包棉花用的废纸写字、演算.他明白，求学问必须循序渐进，持之以恒.要学到真本领，就要花力气，绞脑汁，付出劳动的代价.

日复一日，华罗庚沉醉在数学王国中，有时候顾客喊他听不见，问他答非所问，买香烟他拿来了火柴，要买棉花却给了灯草，因此被人称为“罗呆子”.5年间，华罗庚自学了高中和大学初年级的全部数学课程.

1929年，华罗庚受雇为金坛中学庶务员，并开始在上海《科学》等杂志上发表论文.1930年春，华罗庚在《科学》杂志发表的《苏家驹之代数的五次方程解法不能成立之理由》，轰动数学界，引起了清华大学熊庆来教授的重视.1931年，他被调到清华数学系任助理员，从此踏上了一条通往学术的征途.在清华人才济济的环境中，华罗庚立下一个宏愿：以过人的努力，追求自己的成就.他认为，“天才出于积累，聪明在于勤奋”.基于勤奋与努力，华罗庚在清华只用了5年时间，就从助理员、助教进而到英国剑桥大学研究深造.在进修期间华罗庚一心只求学问，两年里写了10多篇论文，攻克了许多数学难题，深得著名数学家哈代的赞誉.他所写的一篇关于德国著名数学家高斯的论文，为他赢得了世界声誉.

1937年抗战爆发，华罗庚放弃攻读博士学位的机会回到清华担任正教授.南迁昆明后，清华大学、北京大学、南开大学合并组成了西南联合大学，华罗庚被聘请为教授.为躲避日军的频繁轰炸，华罗庚一家曾搬到离西南联大五里地的黄土坡村住下，附近山沟的防空洞成了他的工作间.可是有一天，敌机来了.一个炸弹落下来，防空洞被炸塌，华罗庚被活埋在里面.幸亏当时有两个学生正在附近，马上过来挖土，才把他拉出来.

1939年到1941年，在昆明的一个吊脚楼上，华罗庚在旧民居用香烟筒自制油灯的艰苦环境里，历时2年完成了有名的专著《堆垒素数论》.1946年华罗庚应邀赴美，历任普林斯顿数学研究所研究员、普林斯顿大学和伊利诺伊大学终身教授.

二、学习重方法，严师出高徒

华罗庚的一生是与现代中国数学开拓和发展的历史紧密联系在一起的，他为培养中华人民共和国数学家和骨干队伍做出了杰出贡献.他经常告诫学生，“拳不离手，曲不离口”，要抓住机会学习，就能做到“熟能生巧”.他常说：“必须知道，只有不畏困难，辛勤劳动的科学家，才有可能攀登上旁人没有登上过的峰顶.”

华罗庚认为，求学问就是一个“由薄到厚”和“由厚到薄”的学习过程.“譬如我们读一本书，厚厚的一本书，加上自己的注解，就越读越厚，我们知道的东西也就‘由薄到厚’了.但是这个过程主要是接受和记忆的过程.”后者则是消化和提炼的过程，“即把学到的东西，经过咀嚼、消化、融会贯通，提炼出关键性的问题来”，到这时就会感到这本书变薄了.

中科院数学所初建时，年轻的研究人员像学生一样听课，华罗庚对他们严格要求.每天黎明，他就去他们的宿舍敲门，然后一起讨论问题或是讲课；有时睡到半夜，他会把学生挨个叫起来，把白天所讲题目中发现的问题再讲一遍.他从不讲废话，也不闲扯，谈的都是数学.严师出高徒，短时间内，在华罗庚悉心培养下，以万哲先、陆启铿、王元、陈景润等为代表的年轻人迅速成长起来，共同在中国开创了解析数论、典型群、矩阵几何学等多方面的研究.

三、一心为人民，慷慨掷此身

中华人民共和国成立后，华罗庚放弃国外优厚的待遇，带领家人毅然归国，并在途径中国香港时，写下了《致中国全体留美学生的公开信》，大声疾呼：“朋友们！‘梁园虽好，非久居之乡’，归去来兮”，“为了抉择真理，我们应当回去；为了国家民族，我们应当回去……”归国后，他依然在清华任教，中科院数学所成立后兼任所长.1952年院系调整，清华数学系并入北大，华罗庚才离开清华.

从1965年开始，华罗庚开始思考数学如何直接为经济建设服务的问题，毅然放弃了钟爱的纯粹数学研究，全身心投入数学普及工作中.他选择了以改进工艺为主的“优选法”与改善组织管理的“统筹法”来普及.为了让普通工人能明白，他对这两个方法作了简化，尽量避免数学语言，以最易懂的话语进行讲解.在近20年的时间里，他不顾劳累和年老多病的身体，几乎跑遍了中国所有的省市自治区，传授数学知识和解决实际问题.

1985年6月，华罗庚访问日本，6月12日下午，在东京大学演讲.当演讲结束后，华罗庚在雷鸣般的掌声中坐下来，正当要接受鲜花的时候，突发心肌梗死，倒在讲台上，实践了自己的诺言：“最大的希望就是工作到生命的最后一刻.”人们给他送上挽诗：“将军死在战场，学者死在书房，可敬的你，耗尽心血一腔，光荣地死在科学的讲坛上.”