【摘要】：通过比较二重积分与定积分的定义可知，二重积分与定积分相比有如下类似的性质：性质4.4可以将被积函数中的常数因子提到二重积分的记号外面.即性质4.5被积函数的和（或差）的二重积分等于各个被积函数的二重积分的和（或差）.即性质4.6若有界闭区域D被有限条曲线分割为有限个小闭区域，则在D上的二重积分等于各小闭区域上的二重积分的和.例如，有界闭区域D被分割为两个小闭区域D1、D2，则该性质表示二重积
通过比较二重积分与定积分的定义可知，二重积分与定积分相比有如下类似的性质：
性质4.4 可以将被积函数中的常数因子提到二重积分的记号外面.即
性质4.5 被积函数的和（或差）的二重积分等于各个被积函数的二重积分的和（或差）.即
性质4.6 若有界闭区域D被有限条曲线分割为有限个小闭区域，则在D上的二重积分等于各小闭区域上的二重积分的和.
例如，有界闭区域D被分割为两个小闭区域D1、D2，则
该性质表示二重积分对于积分区域具有可加性.
性质4.7 若在有界闭区域D上，被积函数f（x，y）=1，σ为D的面积，则(www.xing528.com)
该性质的几何意义是：高为1的平顶柱体的体积在数值上等于其底面积.
性质4.8 若在有界闭区域D上，两个被积函数有关系f（x，y）≤g（x，y）则
特别地
性质4.9 设M和m分别是被积函数f（x，y）在有界闭区域D上的最大值和最小值，σ为D的面积，则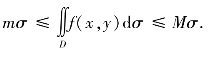
证 根据m≤f（x，y）≤M和性质4.7可知，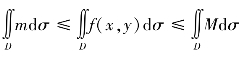
，根据性质4.4和性质4.7可知，
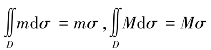，得证.
性质4.10 （二重积分的中值定理）设被积函数f（x，y）在有界闭区域D上连续，σ为D的面积，则在D上至少存在一点（ξ，η）使得下式成立
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
