二重积分：定义与几何意义

1.二重积分的定义

定义4.4　设z=f（x，y）是有界闭区域D上的有界函数，将D任意分割成n个小闭区域σ1，σ2，…，σn，它们所对应的直径分别为d1，d2，…，dn，各小闭区域的面积分别为Δσ1，Δσ2，…，Δσn.在每一个小闭区域σi（i=1，2，…，n）上任取一个点Pi（xi，yi）∈σi，当小闭区域中的最大直径d→0时，若极限存在，则此极限称为函数z=f（x，y）在D上的二重积分，记作即

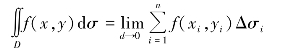
其中称为二重积分号，D称为积分区域，f（x，y）称为被积函数，f（x，y）dσ称为被积表达式，两个自变量x、y称为积分变量，dσ称为面积元素.

在二重积分的定义中，对有界闭区域D的划分是任意的，为了使问题的解决得以简化，在直角坐标系xOy中，我们可以用平行于坐标轴的直线簇来分割D，因此，除了包含边界点的一些小闭区域（求极限时，这些小闭区域可以忽略不计）外，其余的小闭区域都是矩形闭区域，在x与x+Δx和y与y+Δy之间的闭区域面积为Δσ=ΔxΔy（图4.15），为了方便起见，将dσ写成dxdy.于是二重积分也可以记作

与一元函数的定积分的存在性一样，有界闭区域上连续的二元函数的二重积分也一定存在.

根据二重积分的定又可知，曲顶柱体的体积和平面非均匀薄片的质量分别可以表示为如下二重积分的形式

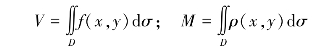(www.xing528.com)

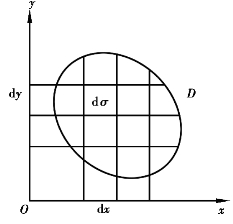
图4.15

2.二重积分的几何意义

若被积函数f（x，y）≥0，二重积分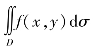在数量上表示以有界闭区域D为底，以二元函数z=f（x，y）为曲顶面的曲顶柱体的体积.

若被积函数f（x，y）≤0，二重积分在数量上

表示以有界闭区域D的底，以二元函数z=f（x，y）为曲顶面的曲顶柱体的体积的相反数.

若被积函数f（x，y）在区域D的若干部分区域上是正的，而在D的其他部分区域上是负的，则被积函数f（x，y）在区域D上的二重积分就等于xOy坐标平面上方部分的曲顶柱体体积与下方部分的曲顶柱体体积的差.