大学应用数学-问题举例揭示曲顶柱体体积的近似计算方法

曲顶柱体的体积　设有一个立体，它的底是xOy坐标平面上的有界闭区域D，它的侧面是以D的边界曲线为准线而母线平行于Oz坐标轴的柱面，它的顶是曲面z=f（x，y），这里f（x，y）≥0并且在区域D上连续（图4.14）.我们将这种立体称为曲顶柱体.空间内由曲面所围成的体积总可以分割成一些比较简单的曲顶柱体的体积的和.下面分析如何计算曲顶柱体的体积V.

图4.14

平顶柱体的体积公式为底面积×高.而曲顶柱体的高是不断变化着的。可以借鉴一元函数的定积分

中求曲边梯形面积的方法来帮助解决曲顶柱体的体积计算问题.对于有界闭区域D上的连续函数z=f（x，y），有：

（1）分割.任意分割D为n个小闭区域σ1，σ2，…，σn，它们所对应的直径为d1，d2，…，dn，各小闭区域的面积分别为Δσ1，Δσ2，…，Δσn，于是曲顶柱体就被分割成了n个小曲顶柱体.(www.xing528.com)

（2）取近似.在每一个小闭区域σi（i=1，2，…，n）上任取一个点Pi（ξi，ηi）∈σi.以该点所对应的函数值f（ξi，ηi）近似代替小曲顶柱体的高，则每一个小曲顶柱体体积的近似值为f（ξi，ηi）Δσi（i=1，2，…，n）.

（3）求和.对这n个小曲顶柱体的体积求和，得曲顶柱体体积的近似值为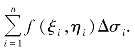

（4）取极限.当分制无限地细密时，则小闭区域的数量就越来越多，小闭区域σi的面积Δσi也就越来越小；当这n个小闭区域中最大的直径d=max{d1，d2，…，dn}趋向于零时，上述和式的极限就是该曲顶柱体的体积V，即

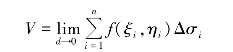
这样，求曲顶柱体的体积问题就归结为求上述和式的极限.事实上，实际应用过程中的许多量的相应改变量问题反映在图像上与上述问题类似.例如，非均匀分布的平面薄片的质量，在图像上反映为以薄片为底，以密度函数ρ（x，y）[ρ（x，y）≥0]为顶的曲顶柱体的体积.