大学应用数学：多元复合函数求偏导数方法

由于可以将多元复合函数视作是一元复合函数的推广，因此，求多元复合函数的偏导数的方法与一元复合函数的求导数的方法类似.利用多元函数全微分的叠加原理，我们可以推导出多元复台函数的偏导数法则.

定理4.2　若函数u=φ（t）及v=ψ（t）都在点t处可导，并且二元函数z=f（u，v）在相对应的点（u，v）处具有连续的偏导数，则复合函数z=f[φ（t），ψ（t）]在点t处可导，并且其导数可用下列公式计算

此复合函数各变量间的关系如图4.12所示，函数与自变量间的路径数与求导数公式中的项数相对应，而每年路径反映的又是函数与自变量之间的复合关系.

必须注意的是：此处函数z的自变量为t，属于一元函数，区别于二元函数的偏导数，此处的叫全导数.

例4.22　已知z=uv，u=sin x，v=ex，求

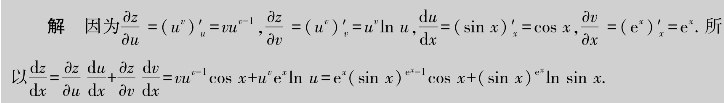
定理4.2中，如果中间变量u，v是二元函数，不妨设u=φ（x，y），v=ψ（x，y），则函数z对自变量的偏导数求法如下.

定理4.3　若二元函数u=φ（x，y）和v=ψ（x，y）在点（x，y）处的偏导数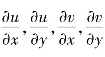都存在，并且在对应的点（u，v）处，二元函数z=f（u，v）具有连续的偏导数，则复合函数z=f[φ（x，y），ψ（x，y）]在点（x，y）处对两个自变量x，y的偏导数存在，并且其导数可用下列公式计算

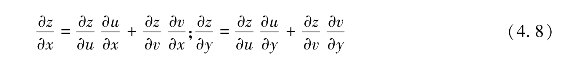
此复合函数的各变量间的关系如图4.13所示.

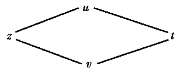
图4.12

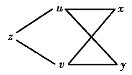
图4.13

例4.23　设z=eusin v、u=xy、v=x+y，求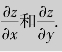

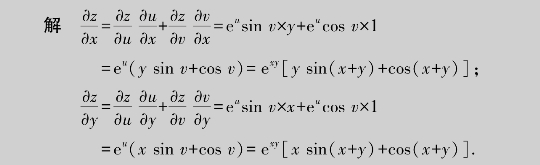
对于比较复杂的幂指型函数，可以通过变量代换将其转化为多元复合函数来求导数.

例4.24　设二元函数z=（x2-2y）xy，求

解　不妨设两个二元函数u=x2-2y，v=xy，则二元函数z=uv.于是

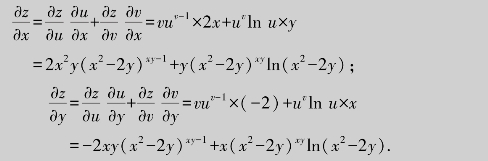
对于多元复合函数来说，如果各函数关系比较简单，也可以将中间变量的解析式直接代入表达式而对自变量直接求偏导数.

例4.25　设二元函数z=ex-2y，而x=sin t，y=t3，求

解　将中间变量x=sin t和y=t3代入函数z=ex-2y，得，应用一元复合函数求导数方法得

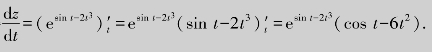
例4.26　已知z=f（x，y）=x2+ln y，而y=sin x，求

解　将中间变量y=sin x代入函数z=x2+ln y，得z=x2+ln sin x，应用一元初等函数求导数方法得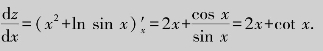

例4.27　设u=f（x，y，z）=e2x+3y-z，而z=x sin y，求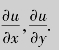(www.xing528.com)

解　将中间变量z=x sin y代入函数u=e2x+3y-z，得u=e2x+3y-x sin y，于是

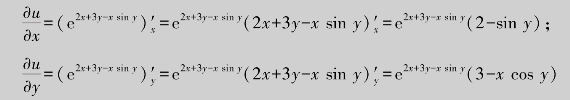
练习4.3

1.填空题

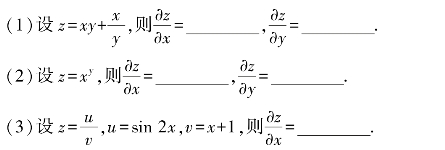
（4）（1.02）3.96的近似值为________，2.032×3.043的近似值为________.

2.选择题

（1）函数z=y cos x在点P（0，1）处的全微分为________.

（A）cos 1dy+dx　　　　（B）dy

（C）sin 1dy+cos 1dx　　　（D）sin 1dy+sin 1dx

（2）如果二阶混合偏导数在区域D内连续，则下列说法错误的是________.

（A）两个二阶混合偏导数相等　　　（B）二次求导所得结果与顺序无关

（C）两次求导顺序不同，所得结果不同　　　（D）二阶混合偏导数与二阶偏导数无关

（3）设函数z=sin（xy2），则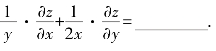

（A）cos（xy2）　　　（B）2ycos（xy2）

（C）2xcos（xy2）　　　（D）ycos（xy2）

（4）二元函数的可微与可导的关系是________.

（A）等价关系（B）可微一定可导

（C）可导一定可微（D）没有条件关系

3.求函数z=2x+3y2在点（2，1）处，当Δx=0.02，Δy=0.01时的全微分和全增量.

4.求下列函数的二阶混合偏导数.

（1）z=x4+y4-4x2y2；　　（2）z=ex sin（x-y）.

5.设函数z=sin（xy），而y=ex，求

6.求下列复合函数的偏导数

（1）z=（x2+y2）xy；　　　（2）