1.定义
设有三个变量x、y、z，当两个变量x、y在一定的范围D内取任意的一组值时，按照确定的对应关系f，变量z都有确定的值与之相对应，则变量z称为两个变量x、y的二元函数，记作z=f（x，y）.其中，变量x、y称为自变量，而变量z则称为因变量（或函数）.自变量x、y的取值范围D称为函数z=f（x，y）的定义域.而函数z=f（x，y）的取值范围称为值域.例如，例4.5中面积S是长x和宽y的二元函数.
2.定义域
由于二元函数的定义域和平面上的点的集合相对应，为了方便起见，我们将平面上由有限条直线或曲线所围成部分的点的集合称为区域.
例如：矩形、扇形、第一象限内等平面上的点集都构成区域.
若区域延伸到无穷远处，则该区域称为无界区域；否则，它总可以被包围在一个以原点为中心而半径适当大的圆内，这样的区域又称为有界区域.围成区域的直线或曲线也称为区域的边界；连同边界在内的区域称为闭区域；不包括边界的区域称为开区域.
例如，D1={（x，y）|x+y＞0}是一个无界的开区域（图4.5）.
D2={（x，y）|x2+y2≤1}是一个有界的闭区域（图4.6）.
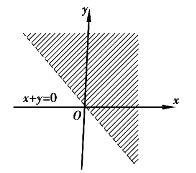
图4.5
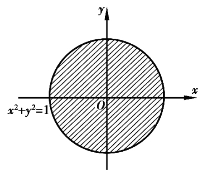
图4.6
二元函数定义域与一元函数定义域的求法相同，当函数的自变量有实际意义时，则应该根据它的实际意义来确定自变量的取值范围；对于那些单纯地由数学解析式所表示的函数而言，使该数学解析式有意义的自变量的取值范围就是该二元函数的定义域.
例4.8 求二元函数
的定义域.
解 要使该二元函数有意义，必须满足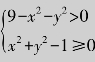
，即1≤x2+y2＜9.故该二元函数的定义域为D={（x，y）|1≤x2+y2＜9}.对应在xOy坐标平面上是以坐标原点为圆心、半径为3的圆与以坐标原点为圆心的单位圆所围成的圆环形区域，但不包括边界线的外圆部分x2+y2=9（图4.7）.
例4.9 求二元函数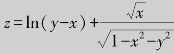
的定义域.(www.xing528.com)
解 要使该二元函数有意义，必须满足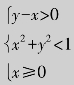
，即该二元函数的定义域为D={（x，y）|y-x＞0，x2+y2＜1，x≥0}，它所对应的区域是一个扇形（图4.8）.
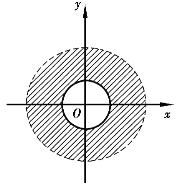
图4.7
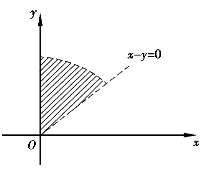
图4.8
3.函数值
对于二元函数z=f（x，y），当给定两个自变量x，y的一组值（x0，y0）时，就可以根据该函数的关系式z=f（x，y）来求出其相应的函数值了，其相应的函数值记作f（x0，y0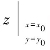），或
，或
例4.10 已如二元函数f（x，y）=x2+2y2-5x+3，求f（0，-2）与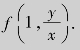
解 f（0，-2）=02+2×（-2）2-5×0+3=11，
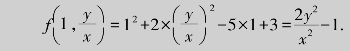
4.圆形
可以将二元函数视作关于三个变量x，y，z的三元方程，它对应的函数图形在空间直角坐标系内表示曲面（或平面）.
例如，二元函数z=Ax+By+D的图形表示平面，函数z和两个自变量x，y之间的关系反映在图形上就是该平面上点的竖坐标与横、纵坐标之间的关系.
函数z=x2+y2的图形表示顶点在原点、开口向着z轴正方向的旋转抛物曲面（图4.9）.
函数
的图形表示球心在原点、半径为R的半个球面（图4.10）.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
