微分方程应用举例：大学应用数学

许多实际问题的数学描述为微分方程问题.在应用过程中，将形形色色的实际问题转化为微分方程的求解问题，其步骤大致如下：

（1）根据实际要求确定要研究的量（自变量、未知函数、必要的参数等）并确定坐标系.

（2）找出这些量所满足的基本规律（物理的、几何的、化学的或其他学科等）.

（3）运用这些规律列出方程和初始条件.

（4）求解微分方程.

例3.42　（传染病的流行问题）设总人数N不变，t时刻得病的人数为x（t），它传染给正常人的传染率为r.

（1）如果不开展宣传运动，任其自然地流行.

（2）为了预防传染病的流行，从t=t0＞0开始持续宣传，使得传染上疾病的人数x（t）减少，减少的速度与总人数N成正比，这个比例也叫宣传强度α.

分析两种情况下传染上疾病的人数.

（1）不采取任何预防措施时，传染人数x（t）所满足的数学模型为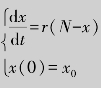，求解这个可分离变量的微分方程，得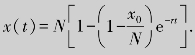

若t→+∞，有这说明，如果不采取任何预防措施，最终每个人都会被传染上疾病.

（2）在宣传强度为α时，传染人数x（t）所满足的数学模型为

得，将初始条件x（t0）代入并整理得

若t→+∞，有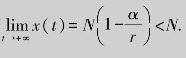这说明，持续而强有力的宣传能有效控制传染病的流行.

练习3.6

1.判断题

（1）（　　）微分方程的解可以是显函数，也可以是隐函数.

（2）（　　）dy=3xdx是一阶微分方程.

（3）（　　）是可分离变量的微分方程.

（4）（　　）y″=f（x，y′）是可降阶的二阶微分方程.

（5）（　　）不是一阶线性微分方程.

2.选择题

（1）满足曲线y=f（x）上点（x，y）处的切线斜率等于该点的横坐标的平方的微分方程是________.

（A）dy=x2　　　　　　（B）dy=x2dx

（C）y′=x2dx　　　　（D）y=x2dx

（2）的通解是________.

（A）y=ln x 　　（B）y=C

（C）y=ln x+C　　（D）

（3）y′+2y-2x=0的通解是________.

（4）若连续函数f（x）满足关系式，则f（x）=________.

（A）ex ln 2　　（B）e2x ln 2

（C）ex+ln 2　　（D）e2x+ln 2

（5）下列方程中可降阶的是________.

（A）y″+xy+y=1　　　（B）y″=xex+y

（C）（1-x2）y″=（1+x）y　　（D）yy″+（y′）2=5

3.填空题

（1）微分方程中未知函数导数的最高阶数，称为微分方程的________.

（2）（y′）2-y2=0的阶数为__________________________.

（3）不显含未知函数y的二阶微分方程y″=f（x，y′），可作代换y′=p，则y″=________可使原方程降阶.

（4）二阶线性齐次微分方程的形式为____________________________________________.(www.xing528.com)

（5）y″-2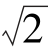y′+2y=0的特征根为________________________________________________.

4.求y′cos x=y满足条件的特解.

5.求y″=x cos x的通解.

6.求yy″=（y′）2的通解.

7.求y″-4y′+3y=0的通解.

8.求作一条曲线，使之通过点（2，3），并且曲线上任一点处的切线夹在两坐标轴之间的线段被切点平分.

9.设某商品的需求价格弹性为-p ln 2，已知该商品的最大需求量为2 000，试求该商品的需求函数Q=Q（p），并求p=3时该商品的需求量是多少?

第3章　自测题

1.判断题

（1）（　　）

（2）（　　）牛顿-莱布尼茨公式揭示了积分学中定积分与不定积分之间的联系.

（3）（　　）

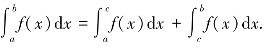
（4）（　　）csc x cot x的原函数是-csc x.

（5）（　　）

2.选择题

（A）sec x+x+C　（B）tan x-x+C

（C）sec x-x+C　　（D）tan x+x+C

（A）f（x）　　（B）f（x）+C　　（C）df（x）　　（D）f（x）dx

（A）-2　　（B）-1　　（C）1　　（D）2

（A）-2　　（B）-1　　（C）1　　（D）2

3.填空题

4.解答题

（4）求曲线y2=2x及直线y=x-4所围成的平面图形面积.

（5）求的右半支曲线及直线y=0，y=1，x=0所围成的平面图形分别绕y轴、x轴旋转一周所形成的旋转体的体积.

（6）设某产品的边际成本为（万元/百台），固定成本C0=1（万元），边际收益R′（Q）=8-Q（万元/百台），求：

①产量从100台增加到500台的成本增量.

②总成本函数C（Q）和收益函数R（Q）.

③产量为多少时利润最大?最大利润是多少?

思政　阅读材料之三

中国古代天文学家与数学

在中国古代灿烂的文明中，天文历法有着相当重要的地位.《尚书·尧典》中曾记载，尧曾组织了一批天文官员到东南西北四个地方去观测天象，以编制历法，预报季节.

下面介绍几位中国古代天文学家在天文研究中应用数学的故事.

东汉天文学家张衡（78—139）从小在数学、地理、文学等诸方面，就表现出了非凡的才能和广博的学识.他在担任太史令时主持观测天象、编订历法、候望气象、调理钟律（计量和音律）等事务.张衡在天文学方面有两项重要贡献，即发表著作《灵宪》和制作浑天仪.《灵宪》中记载了日、月角直径为整个天周的“七百三十六分之一，地广二百四十二分之一”.“七百三十六分之一”，换作现代通用角度单位即为29′21″，如此得到日、月的角直径当为29′35.3″，这和近代天文测量所得的结果误差只有2′左右.

南北朝数学家、天文学家祖冲之（429—500）经过多年的观测和推算，发现过去使用的《元嘉历》存在很大误差.于是祖冲之着手制定新的历法，在公元462年编制成了《大明历》，并于公元510年开始正式颁布施行.

唐朝天文学家张遂（僧一行，673—727）青年时代到长安，研究天文和数学，成为著名学者.为修订历法，测量日、月、星辰在其轨道上的位置并掌握其运动规律，他改进了张衡的“浑天仪”，制造出“浑天铜仪”.他使用“浑天铜仪”和“黄道游仪″观测天象时，可以直接测量出日、月、星辰在轨道上的坐标位置.他推断出天体上的恒星是移动的，这比英国天文学家哈雷（1656—1742）早了一千多年.张遂修订的《大衍历》是一部具有创新精神的历法，他采用不等间距二次内插法推算出每两个节气之间，黄经差相同，而时间距却不同.这种算法基本符合天文实际，这在天文学上是一个巨大的进步.

唐代天文学家、数学家李淳风（602—670），在天文、历法、数学、阴阳学等方面皆有建树，著有《推背图》《乙巳占》.李淳风是世界上第一个给风定级的科学家；注解的《周髀算经》和《古算十经》是世界上最早的数学教材，特别是为宋元时期数学的高度发展创造了条件；《乙巳占》10卷是李淳风的一部重要的星占学著作.李淳风根据他对天文历法的多年研究和长期观测，于麟德二年（665）编成新的历法，命名为《麟德历》.

元朝天文学家、数学家郭守敬（1231—1316）在授时历中对天文数据进行重新测定.他改革的天文计算方法可以归纳为两点：一是全面用内插法三次差计算，即所谓“垛叠招差″；二是引进了球面直角三角形法，即所谓“立浑比量”.