一阶微分方程解法|大学应用数学

1.可分离变量的微分方程

把形如

的微分方程称为可分离变量的微分方程.其特点是函数的导数等于x的变量式与y的变量式的积的形式.

其求解步骤为：

（1）分离变量.将含x的变量式与dx写在等式的一边，含y的变量式与dy分离在等式的另一边，即

（2）两边积分得通解.即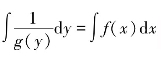，如果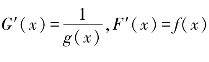，那么通解为G（y）=F（x）+C.

例3.34　1999年我国的国民生产总值（GDP）为80 423亿元，如果能保持每年8%的相对增长率，那么到2010年我国的国民生产总值是多少?

解　以t=0代表1999年，设第t年我国的国民生产总值为P（t），由相对增长率为8%，则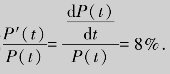

分离变量得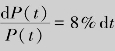，两边积分有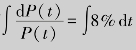，得ln P（t）=0.08t+ln C，即P（t）=Ce0.08t.

将初始条件P t=0=80 423代入通解得C=80 423，所以从1999年起第t年我国的国民生产总值为P（t）=80 423e0.08t，将t=2010-1999=11代入上式，就得2010年我国的国民生产总值为

P（11）=80 423e0.08×11≈193 891.787（亿元）

2.一阶线性微分方程

把形如

的方程称为一阶线性微分方程.其特点是，未知数y及其导数均为一次.当Q（x）≠0时，称为一阶线性非齐次微分方程；当Q（x）=0时，称为一阶线性齐次微分方程.即

它也是可分离变量的微分方程，因此对于一阶线性齐次微分方程，其求解法如下：

分离变量，两边积分，得，通解为

(www.xing528.com)

一阶线性齐次微分方程的解与未知数y的系数有关系.我们也可以通过直接代入公式求解一阶线性齐次微分方程的通解.

对于一阶线性非齐次方程的求解，可用“常数变易法”，就是在其对应的齐次微分方程的通解y=Ce-∫p（x）dx的基础上，将任意积分常数C变易为变量函数C（x），代入一阶线性非齐次微分方程，进一步确定变量函数C（x），得该一阶线性非齐次方程的通解.

求一阶线性非齐次方程通解的具体步骤为

（1）求出对应的齐次微分方程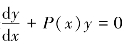的通解为

（2）常数变易.设的通解为

（3）将所设通解代入一阶线性非齐次微分方程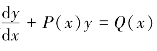，其中，

解得

（4）确定变量函数C（x），得

（5）将变量函数代入所设通解，得一阶线性非齐次方程的通解为

当然，求一阶线性非齐次微分方程的通解，也可以直接代入通解公式

例3.35　求微分方程y′-y cos x=2xesin x的通解.

解　先求对应的齐次方程y′-y cos x=0的通解为

设所求非齐次方程的通解为y=C（x）esin x，则y′=C′（x）esin x+C（x）esin x cos x.

将y=C′（x）esin x+C（x）esin x cos x，y=C（x）esin x代入原方程得C′（x）esin x=2xesin x，即C′（x）=2x，积分得

所以，原方程的通解为y=esin x（x2+C）.