定积分物理学应用-大学应用数学

1.变力沿直线做功

例3.27　弹簧在静止状态下受外力作用拉伸长度为4 cm（弹性限度内），设弹性系数为k，求拉伸过程中外力所做的功.

解　由于弹簧的弹力f与伸长的长度成正比，方向指向平衡位置，且f=-ks，于是外力为

F=-f=ks

选择弹簧伸长量s为积分变量，其取值范围为[0，4]，对于任意s∈[0，4]，在位移区间[s，s+ds]上，功元素为dW=Fds=ksds，于是

例3.28　水下施工前，需将高为10 m、底圆半径为4 m的围堰中的水全部吸出，求外力所做的功.

解　如图3.19所示，取水的深度x为积分变量，其取值范围为[0，10]，对于任意x∈[0，10]，在[x，x+dx]上，外力所做的功近似等于将体积为π×42×dx（m3）的水克服重力移动x m所做的功（功元素），即dW=ρ×π×16×x×dx=16πρxdx，其中水的比重ρ=9.8 kN/m3，于是

2.液体的压力(www.xing528.com)

例3.29　某水库的梯形闸门在水下8 m到12 m，如图3.20所示，梯形上底为6 m，下底4 m，求闸门所受的压力.

解　根据图形的对称性，只需求出半个梯形面上的液体的压力即可，其中梯形的一条腰对应的函数为，取水的深度x为积分变量，其取值范围为[8，12]，对于任意x∈[8，12]，在[x，x+dx]上，小梯形上所受的压强近似看作ρx，面积近似看作小矩形，则压力元素为

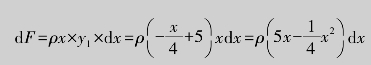
所以，闸门所受的液体的压力为

图3.19

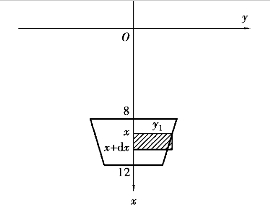
图3.20