大学应用数学教材：定积分的元素法

1.元素法的概念

首先回顾定积分的定义引入过程中求由曲线y=f（x）[f（x）≥0]和直线x=a，x=b，y=0围成的曲边梯形面积的四个步骤：

（1）分割.在[a，b]内任意插入n-1个分点把[a，b]分成n个小区间[xi-1，xi]（i=1，2，…，n），则大曲边梯形被分割成n个小曲边梯形.

（2）取近似.在[xi-1，xi]上任取一点ξi∈[xi-1，xi]，用小矩形的面积f（ξi）Δxi近似代替小曲边梯形的面积，即ΔAi≈f（ξi）Δxi.

（3）求和.将所有的小曲边梯形面积相加，就得出大曲边梯形面积的近似值，即

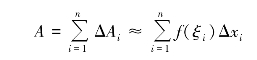
（4）取极限.令λ=max{Δxi}（i=1，2，…，n），于是，当λ→0时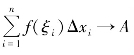，，即

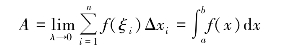
图3.9

在确定积分表达式的四个步骤中，主要是第二步确定小曲边梯形面积的近似值，为了简便起见，用ΔA表示任意[x，x+dx]上的小曲边梯形的面积，而且取该小区间左端点x处对应的函数值f（x）为小矩形的高，则小矩形的面积f（x）dx近似等于小曲边梯形的面积ΔA，即ΔA≈f（x）dx（图3.9中阴影部分），于是将小矩形面积求和并取极限即得曲边梯形的面积，事实上，小矩形的面积f（x）dx就是定积分的被积表达式，将该小矩形的面积f（x）dx称为面积元素，记作dA=f（x）dx，也即

(www.xing528.com)

将上述思想抽象、归纳后形成如下的一般方法：

计算某一数量S，若所求量S与变量x的变化区间[a，b]有关，且关于[a，b]具有可加性，则在[a，b]的任意[x，x+dx]上找出所求部分量的近似值dS=f（x）dx，其中f（x）在[a，b]上连续，然后以它作为被积表达式，从而得到所求量的积分表达式

这种方法称为元素法（或微元法），dS=f（x）dx称为S的元素（或微元）.

2.元素法的具体步骤

（1）根据问题的具体情况，选取一个变量（如x）为积分变量，并确定它的变化区间[a，b].

（2）在[a，b]上任取[x，x+dx]，以点x处对应的函数值f（x）与dx的乘积f（x）dx为所求量A的元素dA，即dA=f（x）dx.

（3）以所求量A的元素dA=f（x）dx为被积表达式，在[a，b]上求定积分，得

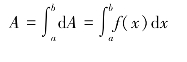
这就是所求量A的积分表达式.