牛顿-莱布尼茨公式：大学应用数学

定理3.6说明，积分上限函数Φ（x）是连续函数f（x）的一个原函数.根据原函数的性质，设F（x）为f（x）的另一原函数.则有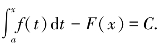当x=a时，有C=-F（a），即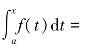F（x）-F（a）.当x=b时，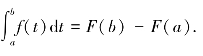

于是有下面定理.

定理3.7　若函数F（x）是连续函数f（x）在[a，b]上的一个原函数，则

这个定理称为微积分基本定理，这个公式称为牛顿-莱布尼茨（Newton-Leibniz）公式，它揭示了定积分与不定积分的内在联系，也表明：一个连续函数在[a，b]上的定积分等于它的任一原函数在[a，b]上的增量.即要计算定积分只需寻找被积函数的一个原函数，再计算原函数在[a，b]上的增量即可.该公式为定积分的计算提供了有效简便的方法.

必须注意的是：牛顿-莱布尼茨公式的运用条件是被积函数f（x）在[a，b]上连续.

例3.16　计算下列定积分.

例3.17　求函数y=sin x在[0，π]上与x轴所围成的图形的面积.

解　由定积分的几何意义知，所求面积等于y=sin x在[0，π]上的定积分.即

练习3.3

1.填空题.

（3）若连续函数f（x）满足，则f（x）=________

.

（4）设函数，则f′（x）=________

.(www.xing528.com)

（5）若连续函数

（6）设

2.选择题.

（1）不能直接使用微积分学的基本公式的是________.

（2）设，则f（x）________.

（A）e2x　　（B）2e2x

（C）2xe2x-1　　（D）2xe2x

（3）定积分

（A）f（6）-f（3）　　　（B）3[f（2）-f（1）]

3.求下列各极限.

4.计算下列定积分.