根据定积分的定义及极限运算法则可得定积分具有如下性质.
性质3.3 两个函数代数和的定积分等于它们定积分的代数和,即
![]()
此性质可推广到有限个函数代数和的情形.
性质3.4 被积函数中的常数因子可以提到积分号外,即
![]()
性质3.5 若在[a,b]上f(x)=k(k为常数),则
![]()
特别地,当k=1时,有![]()
性质3.6 若把[a,b]分为[a,c]和[c,b]两部分,则有
![]()
这个性质表明定积分对于积分区间具有可加性.
实际上,无论a,b,c三点的相对位置如何,性质4仍然成立.例如,当a<b<c时,由性质4知![]() 于是
于是
![]()
性质3.7(比较性质) 若在[a,b]上有f(x)≥g(x),则
![]()
该性质说明,要比较相同区间上定积分的大小,只要比较被积函数的大小即可.
推论3.1 若在[a,b]上f(x)≥0,则![]()
推论3.2 若a<b,则![]()
性质3.8(估值性质) 设M和m分别是f(x)在[a,b]上的最大值和最小值,则
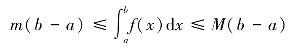
性质3.9(积分中值定理) 若f(x)在[a,b]上连续,则在[a,b]上至少存在一点ξ,使
![]()
积分中值定理的几何解释:在[a,b]上至少存在一点ξ,使得由曲线y=f(x)(f(x)≥0),直线x=a,x=b及x轴所围成的曲边梯形的面积,恰好等于同一底边而高为f(ξ)的矩形的面积(图3.7).f(ξ)称为连续函数f(x)在[a,b]上的平均值,即
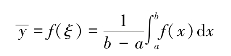
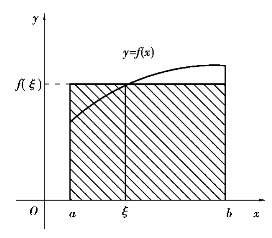
图3.7(https://www.xing528.com)
例3.13 比较下列积分值的大小.
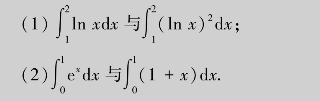
解 (1)由于在[1,2]上0≤ln x<1,所以ln x≥(ln x)2,故有
![]()
(2)令f(x)=ex-(1+x),则f′(x)=ex-1,因为在[0,1]上f′(x)≥0,即f(x)单调增加,所以对任意x∈[0,1],都有f(x)≥f(0)=0,即ex-x-1≥0⇒ex≥x+1,故有
![]()
例3.14 估计定积分![]() dx值的范围.
dx值的范围.
解 因为![]() ,令f′(x)=0,得驻点x=0,又因f(0)=1,f(-1)=e-1,f(2)=e-4,故有m=e-4,M=1,由估值性质得
,令f′(x)=0,得驻点x=0,又因f(0)=1,f(-1)=e-1,f(2)=e-4,故有m=e-4,M=1,由估值性质得![]()
练习3.2
1.填空题.
(1)某物体以速度v=gt(m/s)作自由落体运动,该物体运动10 s后所经过的路程用定积分可以表示为________.
(2)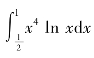 的符号是________.
的符号是________.
(3)若函数f(x)在[-1,1]上连续,且![]() ,则
,则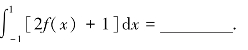
2.选择题.
(1)定积分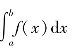 是________.
是________.
(A)一个常数 (B)一个函数族
(C)f(x)的一个原函数 (D)一个非负常数
(2)设函数f(x)在[a,b]上连续,则![]() 的值为________.
的值为________.
(A)小于0 (B)大于0
(C)等于0 (D)不能确定
(3)下列不等式中,成立的是________.
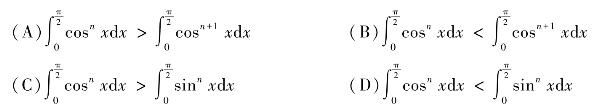
(4)设函数y=f(x)在[a,b]上连续,则曲线y=f(x)与直线x=a,x=b及x轴所围成的平面图形的面积等于________.

3.利用定积分的几何意义说明下列定积分等式.
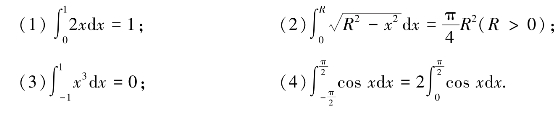
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




