大学应用数学-不定积分的积分法

利用基本积分公式及不定积分的性质，只能计算出少量简单函数的不定积分，因此还需要进一步研究不定积分的计算方法.常用的基本积分法是换元积分法和分部积分法，本节将讨论不定积分的第一、二类换元法和分部积分法.

1.第一类换元积分法（凑微分法）

在微分法中，复合函数的微分法是一种重要的方法，积分法作为微分法的逆运算，也有相应的方法，就是换元积分法.

定理3.3　若，且u=φ（x）具有连续导数，则

这种求不定积分的方法叫作第一类换元积分法（或凑微分法）.凑微分法的关键是把被积表达式凑成f[φ（x）]dφ（x）的形式.下面通过例子介绍凑微分法的思路.

例3.3　求下列不定积分.

解　（1）对照基本积分公式表，上式与公式（3）相似，为此将dx写成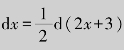，代入式中，有

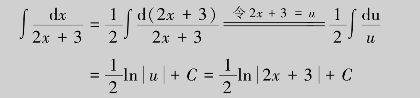
（2）上式与基本积分公式表中公式（2）相似，为此将xdx写成代入式中，有

若变量代换的过程熟练以后，则可以不写出中间变量u.第一类换元积分法的关键是通过凑微分寻找变换u=φ（x），从而将原积分化为关于u的简单积分，再套用基本积分公式求解.

现将凑微分时常用的微分式列举如下（其中a，b为常数，且a≠0）：

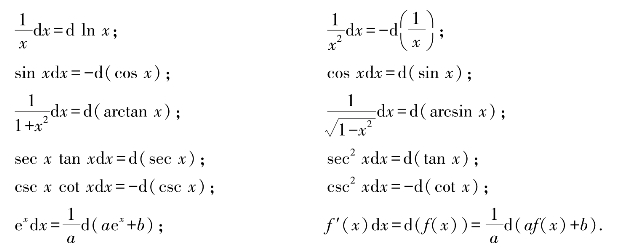
在凑微分时，要具体问题具体分析，应在熟记基本积分公式和常用凑微分式子的基础上，通过不断练习，才能掌握这一重要的积分法.

例3.4　求下列不定积分.

类似地，可得

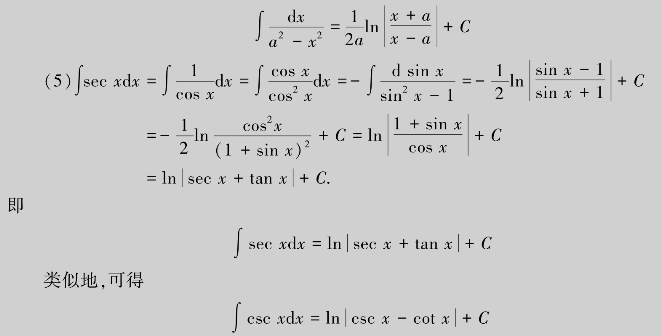
本例题得到的这几个积分以后经常用到，可以作为公式使用.

2.第二类换元积分法（拆微分法）

第一类换元积分法是通过变换u=φ（x），将积分转化为积分但对于某些带根号的无理式的积分，第一类换元积分法无法完成.此时需要作相反的代换，即令x=φ（t），将积分化为积分这就是下面要讨论的第二类换元积分法.

定理3.4　设函数f（x）连续，x=φ（t）单调、可导，且φ′（t）≠0.若∫f[φ（t）]φ′（t）dt=F（t）+C，则

其中t=φ-1（x）是x=φ（t）的反函数.

通常把这种换元积分法称为第二类换元积分法，又称为拆微分法.

第二类换元积分法的关键在于合理选取变量代换x=φ（t），消去被积函数中的根号，使积分的计算简单化.下面举例说明第二换元积分法常用的几种变量代换.

（1）根式代换.若被积函数中含有根式，一般可作变量代换，消去根式.

例3.5　求下列函数的积分.

解　（1）为了消去被积函数中的根式，令，则，dx=t2dt，于是有

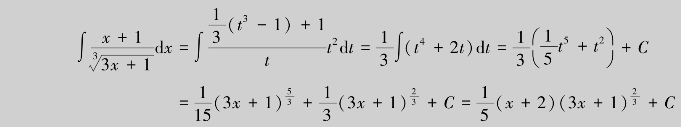
（2）为了同时消去两个异次根式，可令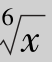=t，则x=t6，dx=6t5dt，于是有

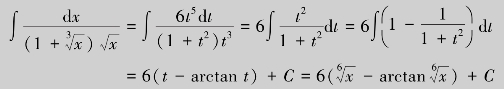
（2）三角代换.

例3.6　求下列函数的积分.

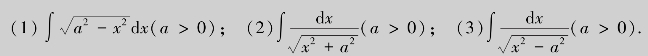
解　（1）为了消去被积函数中的根号，使两个量的平方差等于另外一个量的平方，我们联想到同角三角函数的平方关系式sin2x+cos2x=1.为此，设，则dx=a cos tdt，于是有

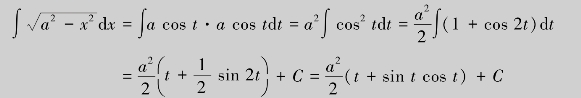
回代，将变量t换为x.为简便起见，根据代换x=a sin t做辅助直角三角形（图3.2）.由于因此

（2）为了消去被积函数中的根号，利用1+tan2 t=sec2 t.设x=a tan t，则dx=a sec2 tdt，，于是有

根据代换x=a tan t做辅助直角三角形（图3.3）.由于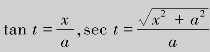，因此

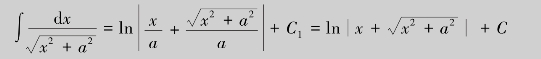
其中C=C1-ln a.

（3）为了消去被积函数中的根号，利用sec2 t-1=tan2 t.设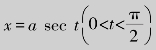，则dx=a sec t tan tdt，，于是有

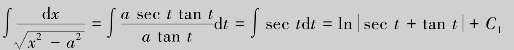
根据代换x=a sec t做辅助直角三角形（图3.4）.由于，因此

其中C=C1-ln a.

一般地，当被积函数含有

图3.2

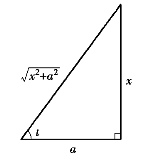
图3.3

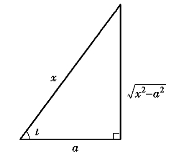
图3.4

（3），可作代换

通常称以上代换为三角代换.具体解题时，对具体问题要具体分析，不要拘泥于上述三角代换，选取尽可能简捷的代换.例如，就不必用三角代换，而用凑微分更为方便.

3.分部积分法

在复合函数求微法则的基础上得到了换元积分法，但当被积函数为两种不同类型的初等函数的乘积时，换元积分法不一定有效.下面将利用两个函数乘积的微分法则来推导计算不定积分的另一种方法——分部积分法.(www.xing528.com)

设函数u（x），v（x）具有连续导数，由两函数乘积的微分公式d（uv）=udv+vdu，得

udv=d（uv）-vdu

两边积分得

称该公式为分部积分公式.这个公式把积分∫udv转化为∫vdu，当后一个积分比前一个积分容易计算时，分部积分公式就可以起到化难为易的作用了.当遇到被积函数为两种不同类型的初等函数乘积形式时，常应用分部积分公式.

例3.7　求

解　被积表达式x cos xdx可分解为x与cos xdx的乘积.设u=x，dv=cos xdx=d sin x，从而v=sin x，于是有

若选取u=cos x，dv=x d x，则

结果被积函数中x的幂升高了，积分的难度反而增大.由此可见，如果u和dv选取不当，就可能使不定积分的计算变得困难，所以运用分部积分法时，恰当选取u和dv是一个关键.选取u和dv应使不定积分的计算更简便，一般应考虑下面两点：

（1）v要容易求得（可用凑微分法求出）；

（2）∫vdu要比∫udv容易计算.

例3.8　求下列函数的积分.

解　（1）设u=x，dv=ex dx=dex，则

在熟练以后，略去u，v的形式而直接计算.

当被积函数只有一个因子而又不能使用换元积分法时，可用分部积分法.并且在应用分部积分法时，常用到下面的规律：

（1）对于等，选取u=xn；

（2）对于等，选取u=ln x，arccos x，arctan x；

（3）对于等，选取u=eax，sin bx，cos bx均可，需采用“循环解出”的策略.在使用多次分部积分法后，出现“循环现象”.此时，可将该算式看成一个所求积分的方程，解出该积分即可.

例3.9　求

例3.10　求

例3.11　求

将再次出现的移至左端，整理得所求积分为

必须注意的是：（1）因为不定积分代表全体原函数，循环解出时，特别注意加上任意常数C.

（2）有时换元积分法和分部积分法在求积分运算时往往同时使用.

例3.12　求

解　令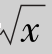=t，则x=t2，dx=2tdt，于是

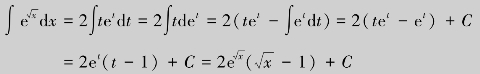
练习3.1

1.填空题

（1）d________=3dx，

（2）设x3为f（x）的一个原函数，则df（x）=________；

（3）已知，则f（x）=________；

（4）

2.选择题

（1）设f（x）是可导函数，则

（A）f（x）　　　　　（B）f（x）+C

（C）f′（x）　　　　（D）f′（x）+C

（2）设f（x）是连续函数，且，则下列各式正确的是________.

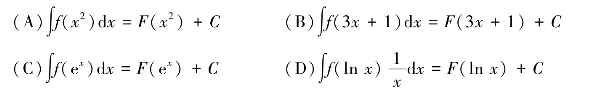
（4）若f′（x）=g′（x），则下列式子一定成立的是________.

（5）

（A）f（x）+C　　　　（B）f′（x）+C

（C）xf（x）+C　　　（D）f2（x）+C

3.求下列不定积分

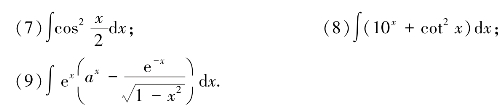
4.一曲线通过点（e2，3），且在任一点处的切线斜率等于该点横坐标的倒数，求该曲线的方程.

5.利用换元积分法求下列不定积分.

6.利用分部积分法求下列不定积分.

7.设f′（ex）=1+x，求f（x）.

8.已知f（x）的原函数为ln2x，求

9.某商品的需求量θ为价格P的函数，该商品的最大需求量为1 000，已知需求量的变化率为，求该商品的需求函数.