大学应用数学：不定积分概念与性质

1.不定积分的概念

定义3.1　若在区间I上可导函数F（x）的导函数为f（x），即对任一x∈I，都有

F′（x）=f（x）或dF（x）=f（x）dx

则称函数F（x）为f（x）在区间I上的原函数.

例如，由于（sin x）′=cos x，所以sin x是cos x的原函数；又由于（x2）′=2x，（x2+1）′=2x，（x2+C）′=2x（C为任意常数），所以x2，x2+1，x2+C都是2x的原函数.

研究原函数必须解决以下两个问题：

（1）一个函数的原函数在什么条件下存在?若存在，是否唯一?

（2）若已知某函数的原函数存在，如何求出原函数?

关于第一个问题，有下面的两个定理；至于第二个问题，则是本章要介绍的各种积分法.

定理3.1　若函数f（x）在区间I上连续，则函数f（x）在区间I上存在原函数F（x）.

由于初等函数在其定义域内连续，所以由定理3.1知，初等函数在其定义域内存在原函数.

定理3.2　若F（x）是函数f（x）在区间I上的一个原函数，则函数f（x）有无穷多个原函数，且它们彼此相差一个常数.

定理3.2说明，若一个函数有原函数，则它必有无穷多个原函数，且它们彼此相差一个常数.所以，要求函数f（x）的所有原函数，只需求出函数f（x）的一个原函数F（x），然后再加上任意常数C，即用F（x）+C表示函数f（x）的所有原函数.

定义3.2　若函数F（x）是f（x）在区间I上的一个原函数，则函数f（x）的全体原函数F（x）+C称为f（x）在区间I上的不定积分，记做∫f（x）dx，即

f（x）dx=F（x）+C

其中记号“”称为积分号，f（x）称为被积函数，f（x）dx称为被积表达式，x称为积分变量，C称为积分常数.

例3.1　求下列不定积分.

解　（1）由于（sin x）′=cos x，所以

（2）由于

（3）由于

（4）当x＞0时，；当x＜0时，，所以(www.xing528.com)

函数f（x）的一个原函数F（x）的图形称为f（x）的一条积分曲线.显然y=F（x）+C的图形是由曲线y=F（x）沿y轴方向上、下任意平行移动而得到的无穷多条曲线构成的曲线族，称为函数f（x）的积分曲线族，这就是不定积分的几何意义.在积分曲线族中，所有曲线在横坐标相同的点处的切线相互平行（图3.1）.

图3.1

求不定积分的运算叫作积分运算，积分运算与微分运算互为逆运算，具有如下关系：

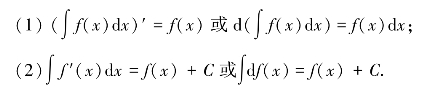
2.基本积分公式

由于积分运算是微分运算的逆运算，所以由导数的基本公式得到基本积分公式.为方便起见，现将基本积分公式列表如下：

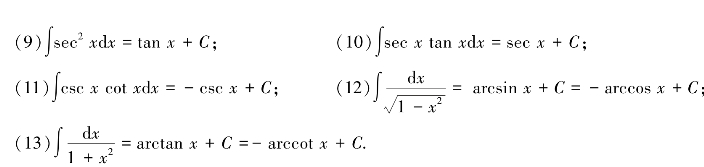
以上13个基本积分公式是求不定积分的基础，学习时应与相应求导公式对照记忆.

3.不定积分的性质

由不定积分的定义可以推得不定积分具有下列性质：

性质3.1　设函数f（x）的原函数存在，k为非零常数，则

性质3.2　设函数f（x）与g（x）的原函数都存在，则

例3.2　求下列不定积分.

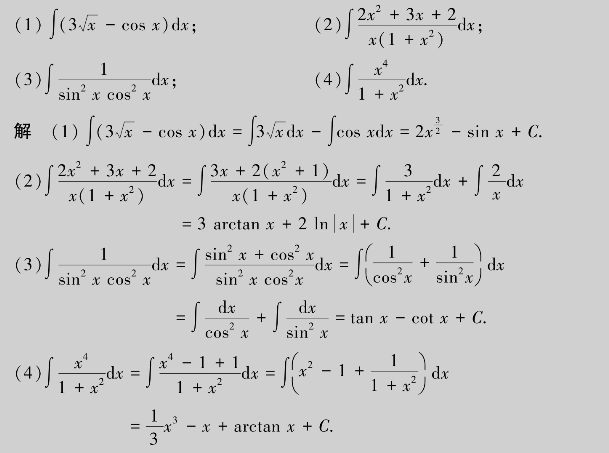
必须注意的是：（1）分项积分后，不必在每个积分结果中都“+C”，只需总的加一个常数C即可.

（2）为了检验积分结果是否正确，可将积分结果求导，看是否等于被积函数即可.