微分在近似计算中的应用-大学应用数学

1.函数增量的近似值

根据前面的分析，对于可导函数，当|Δx|很小时，可以用函数的微分dy近似代替函数的增量Δy，即Δy≈dy=f′（x）dx.

例2.40　一半径为10 cm的金属圆片加热后，半径增加了0.02 cm，求面积增量的近似值.

解　圆的面积A是半径r的函数，即A=πr2，于是dA=d（πr2）=2πrdr.

当r=10 cm，dr=0.02 cm时，函数的微分为dA=2π×10×0.02=0.4π.

因为Δr=0.02 cm很小，所以ΔA≈dA≈1.256 cm2.

2.函数的近似值

对于可导函数y=f（x），当自变量由x变化到x+Δx时，如果|Δx|很小，函数的增量与微分近似相等，即Δy=f（x+Δx）-f（x）≈dy，于是有

f（x+Δx）≈f（x）+f′（x）Δx

这说明，函数在点x附近（x+Δx）的函数值f（x+Δx）近似等于函数在点x处的函数值与函数在该点处的微分之和.

例2.41　计算sin 30° 30′的近似值.(www.xing528.com)

解　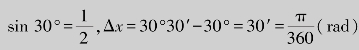，当时，函数y=sin x的微分为

由近似公式f（x+Δx）≈f（x）+f′（x）Δx，可知

3.常用的近似计算公式

当|x|很小时，用近似等式f（x）≈f（0）+f′（0）x可推导出下面几个常用的近似公式：

（1）sin x≈x（x以弧度为单位）；　　（2）tan x≈x（x以弧度为单位）；

（3）arcsin x≈x；　　　　（4）arctan x≈x；

（5）ln（1+x）≈x；　　　　（6）ex≈1+x；

例2.42　求下列近似值.

（1）e0.02；　　　（2）

解　（1）e0.02≈1+0.02=1.02.