1.微分的定义
设函数y=f（x）在点x的某个邻域内有定义，当自变量由x变化到x+Δx时，如果相应函数的增量Δy能表示为Δy=AΔx+o（Δx），其中A与Δx无关.则称函数y=f（x）在点x处可微，并将Δy的线性主部AΔx称为函数y=f（x）在点x的微分，记作dy，即
dy=AΔx
如果将等式Δy=AΔx+o（Δx）两边同时除以Δx，得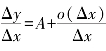
，当Δx→0时，得f′（x）=A.所以，函数y=f（x）在点x处的微分公式为
dy=f′（x）Δx
当函数y=x时，函数的微分dy=dx=x′Δx=Δx，即dx=Δx，于是函数y=f（x）的微分可以写成
dy=f′（x）dx.
如果将等式dy=f′（x）dx两边同时除以dx，即得
.
必须注意的是：（1）函数的微分等于函数的导数与自变量微分之积.根据导数公式和运算法则可以推导微分公式和运算法则.（2）上述等式也表明函数y=f（x）的微分与导数之间的关系，即可导的点一定可微，可微的点也一定可导.（3）函数在某点的导数
可以看作是函数的微分与自变量微分的商，所以导数也称为微商.（4）对于可导函数，当自变量的增量的绝对值比较小（或|Δx|→0）时，可以用函数的微分dy近似代替函数的增量Δy.（5）微分与导数虽然有着密切的联系，但他们具有本质区别：导数是函数在一点处的变化率，而微分是函数在一点处由自变量增量所引起的函数增量的主要部分；导数的值只与x有关，而微分的值与x和Δx都有关.
例2.38 设函数y=x3，求当x=1，Δx=-0.01时函数的微分和增量.
解 因为y′=（x3）′=3x2，所以dy=y′dx=y′Δx，将x=1，Δx=-0.01代入上式即得函数在该点的微分为(www.xing528.com)
dy=3×（-0.01）=-0.03
而函数的增量为
Δy=（1-0.01）3-13=-0.03+0.003=-0.029 7
可见，当|Δx|比较小时，dy与Δy很接近.
2.微分的几何意义
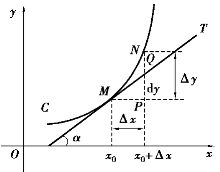
图2.8
设可导函数y=f（x）的图像是一条曲线，如图2.8所示，对于任一自变量x0，在曲线上对应点为M（x0，y0），当自变量变化到x0+Δx时，对应曲线上的点为N（x0+Δx，y0+Δy），过点M作曲线的切线MT，倾斜角为α，因tan α=f′（x），故
f′（x）Δx=dy=PQ
因此，微分的几何意义是函数曲线的切线上纵坐标的改变量.当|Δx|很小时，我们用函数的微分近似代替函数的增量，也就是用切线段MT上纵坐标的增量代替曲线段MN上纵坐标的增量.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
