与极值不同,最值是一个整体概念,它是指自变量在某确定范围内对应的函数值比较大小,最大值和最小值统称为最值,使函数取得最值的点称为最值点.
1.闭区间上连续函数的最值
从图2.5可以看出.闭区间[a,b]上的连续函数y=f(x)的最大值和最小值只有可能在区间端点和极值点处取得.因此,我们只需要比较区间端点处与可能极值点处对应的函数值的大小即可,其中,最大的那个值就是[a,b]上的连续函数y=f(x)的最大值,最小的那个值就是[a,b]上的连续函数y=f(x)的最小值.
例2.23 求函数![]() 在[-2,2]上的最大值与最小值.
在[-2,2]上的最大值与最小值.
解 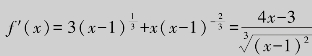 .显然,x=1为不可导点;令f′(x)=0,得驻点为
.显然,x=1为不可导点;令f′(x)=0,得驻点为![]() ,计算并比较以下几个函数值的大小:
,计算并比较以下几个函数值的大小:
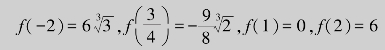
所以,函数![]() 在[-2,2]上的最大值为
在[-2,2]上的最大值为![]() ,最小值为
,最小值为![]()
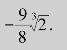
2.开区间内可导函数的最值
开区间内可导函数的极值点就是驻点,所以,开区间内可导函数的最值点就在驻点处.在实际应用问题中,如果可导函数的最值存在,且函数在所考虑的区间内只有一个驻点,则该驻点就是函数的最值点.
 (https://www.xing528.com)
(https://www.xing528.com)
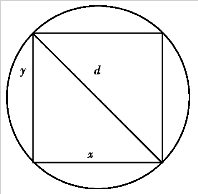
图2.6
例2.24 横截面为矩形的梁,它的强度与矩形的长和宽的平方的乘积成正比.现在要把直径为d的圆柱形木材加工成横截面为矩形的梁,如图2.6所示.若要使梁有最大的强度,问矩形的长和宽之比应是多少?
解 设梁的横截面的长为x,宽为y,梁的强度为η,则
η=kxy2(k为比例系数)
由于y2=d2-x2(0<x<d),代入上式得η=kx(d2-x2),求导数得η′=k(d2-3x2),令η′=0,得驻点为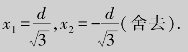
由于梁的最大强度一定存在,且在(0,d)内取得,所以当![]() 时,梁的强度η最大,此时,
时,梁的强度η最大,此时,![]() ,所以,当长和宽的比
,所以,当长和宽的比![]() 时,强度最大.
时,强度最大.
例2.25 设某厂生产某种产品x吨时,其销售收入为![]() (万元),成本函数为
(万元),成本函数为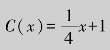 (万元),求总利润达到最大时的产量x.
(万元),求总利润达到最大时的产量x.
解 设总利润函数为L(x),则有L(x)=R(x)-C(x)=![]() ,求导数得L′(x)=
,求导数得L′(x)=![]() .令L′(x)=0,得驻点为x=64.由于最大利润一定存在且在(0,+∞)内,所以当产量x=64吨时利润最大,此时最大利润为L(64)=15(万元).
.令L′(x)=0,得驻点为x=64.由于最大利润一定存在且在(0,+∞)内,所以当产量x=64吨时利润最大,此时最大利润为L(64)=15(万元).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




