汽车广告制作成本分析及观众增加效果

例1.25　某汽车公司做30分钟的广告，其内容为：一段喜剧小品、一段音乐、至少3分钟的广告.电视台规定，30分钟节目中的广告时间不得超过12分钟，且无论如何不得超过喜剧小品的时间，又喜剧小品的时间不得超过20分钟，其余时间演奏音乐.播放成本：喜剧小品150元/分钟、音乐100元/分钟、广告50元/分钟.由经验知，播1分钟的喜剧，增加4 000观众，播1分钟的音乐，增加2 000观众，播1分钟的广告，减少1 000观众.汽车公司希望：在付出最少成本的情况下获得最多的观众.问：如何分配节目播出时间，才能满足汽车公司的需求?

解　模型准备　考虑观众人数与节目类型的关系，播出成本与节目类型和时间的关系，从而收集相关数据，如题目中给出的数据.

模型假设　观众人数的变化影响中，忽略其他媒体、社会因素或自然因素的影响；对于具体的节目类型观众的影响中，也忽略节目的相对差异性等.

模型建立　假设播放喜剧的时间为x（分钟），播放广告的时间为y（分钟），播放音乐的时间为30-x-y（分钟），则

观众人数　N=4 000x+2 000（30-x-y）-1 000y=60 000+2 000x-3 000y.

成本　C=150x+100（30-x-y）+50y=3 000+50（x-y）.

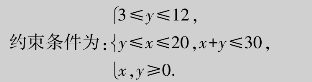
模型求解　如图1.18所示，将约束条件反映在多边形中，分析成本函数可知，成本最小值3 000元在线段AB上取得.

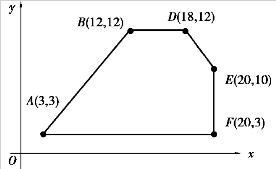
图1.18

在点A处，NA=57 000人；

在点B处，NB=48 000人.

同样的成本，在点A处观众最多，所以，可以建议汽车公司节目播出时间安排为：喜剧与广告各3分钟，音乐24分钟，这样，在成本最少的情况下，观众人数最多.

模型分析与检验　对于该模型的解决方案，由于数据的收集有限，因而，不一定是使30分钟广告达到最大收益的广告策略.如果能够进一步收集与分析观众人数与产品销售量之间的关系，就可以找出在现有条件下的最优投人产出比，使汽车公司获得最大的收益.

模型的应用　此模型适用于在一定的广告费用情况下如何分配节目时间，使观众人数最多的问题.

练习1.5

某企业有下面4个投资机会

项目A：从第1年到第4年每年年初需投资，并于次年年末回收本利115%；

项目B：从第3年年初需要投资，到第5年末回收本利125%，但规定最大投资额不超过50万元；

项目C：第2年年初需要投资，到第5年末才能回收本利140%，但规定投资额不超过60万元；

项目D：5年内每年年初买公债，于当年末归还，年利率6%.

企业现有资金100万元，问应如何确定每年给这些项目投资，使到第5年末拥有资金的本利总额最大?请你为企业建立最优投资方案的数学模型.

第1章自测题

1.填空题

（1）若函数f（x）的定义域为[0，1]，那么f（2x+1）的定义域为________.

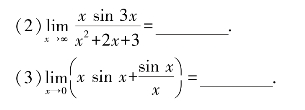
（4）设x→0时，ln（1-x）与eax-1是等价无穷小，则a=________.

（5）设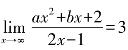，则a=________，b=________.

（6）设f（x）在x=2处连续，且，则f（2）=________.

2.选择题

（1）下列函数在定义域内有界的是________.

（2）设

（A）1　　（B）-1　　　（C）0　　（D）不存在

（3）若

（4）函数间数点的个数为________.

（A）0个　　（B）1个　　（C）有限多个　　（D）无穷多个

（5）x=-1是函数的________间断点.

（A）跳跃　　（B）可去　　（C）无穷　　（D）震荡

（6）已知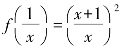，则f（x）=________.

3.计算题

（1）求下列极限.

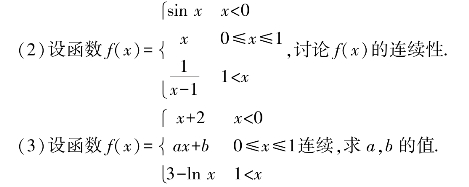(www.xing528.com)

（4）证明方程x3+3x-1=0至少有一个小于1的正根.

思政　阅读材料之一

数学到底有多重要

2019年7月22日，《人民日报》在新浪微博上发布了一条官微，钦点了“无处不用”的数学：“数学到底有多重要?这个学科影响国家实力！宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，生物之谜，日用之繁，无处不用数学.”近日，科技部、教育部、中科院、自然科学基金委联合印发《关于加强数学科学研究工作方案》.统计计算、模型算法……数学不止用于星空之上，也用于社会之中.为何要学数学?或许，这就是答案.

（1）数学与航空航天

•世界上任何一枚火箭的设计制造，都离不开一个公式

齐奥尔科夫斯基公式，1903年，由俄国科学家康斯坦丁·齐奥尔科夫斯基提出.这个公示是关于火箭飞行速度同火箭发动机喷气速度、火箭质量、燃料质量关系.

•航天器何时发射是可以算出来的

航天器发射时间限制条件繁多，包括光照条件、回收时间、交会对接等等.通过建立每个限制条件和发射时间之间的计算公式，可分别计算出相应的发射窗口，取其共同部分便是航天器最终的发射时间.

（2）数学与国防安全

•定量化分析、建模用于现代化战争

大到战役指挥，小到作战方案，都需要进行定量化分析，建立模型，形成随机应变的作战指挥系统.其中概率统计、运筹学等数学分支发挥着重要作用.

•数论用于信息的“加密”与“解密”

公开密钥算法大多基于计算复杂度很高的难题，求解需要在高速计算机上耗费许多时日才能得到答案.这些方法通常来自于数论.例如，RSA源于整数因子分解问题，DSA源于离散对数问题，而椭圆曲线密码学则基干与椭圆曲线相关的数学问题.

（3）数学与生物医药

•生命现象可以通过数学模型研究

数学模型能定量描述生命物质运动过程，一个复杂的生物学问题借助数学模型能转变成数学问题，通过对数学模型的逻辑推理、求解和运算，就能够获得客观事物的有关结论，达到对生命现象进行研究的目的.

•用数学辅助精准医疗

浙江大学一团队通过数学模型和数学算法，不仅能重构病人腹部三维，还编成软件呈现给医生，帮助进行精准判断.他们还利用深度学习处理超声影像，同时加入旋转不变性等现代数学的概念，研制出基于超声影像的智能诊断系统的DE超声机器人.

（4）数学与信息

•没有快速傅里叶变换，就没有当今互联网

在主要信息学科的建立和发展中，一些著名数学家往往成为相关领域的开创者.没有快速傅里叶变换就没有当今互联网；谷歌的核心技术就依赖于大型矩阵特征值的快速算法.

•解决物联网中的关键科学问题

提出并发展具有原创性的理论和方法，给出具有实时性、精确性、智能性和鲁棒性的分布式网络算法，有助于解决以物联网为代表的网络优化与控制技术中的关键科学问题，包括网络资源的有效分配等.

（5）数学与能源

•偏微分方程组、几何学关乎电的安全

很大一片地区联成由若干电网组成的大电网.每个电网由若干发电厂支持，每个发电厂的生产过程都可用微分方程组描述，用高阶代数方程作为约束条件.发电与供电、输电的安全问题涉及复杂的偏微分方程组、几何学等多方面数学问题.

•数学也能用于油气勘探

由于油气资源的勘探日益复杂，利用大型的计算机和先进的数学方法处理油气勘探地震资料，已经成为国内外油气勘探的最重要的手段.

（6）数学与海洋

•大数据实现天气预报

动力系统、偏微分方程、随机微分方程、计算方法等研究方向在大气与海洋科学的研究中都有重要应用.例如，深圳打造的海洋大数据系统，通过数据融合和交织分析，能给出指定区域的出行建议，并能预测台风登陆行径，为专家决策提供依据.

•数学模型可以预测海啸

数学模型通过估计海啸登陆的地点、海浪的高度，以及海浪前进的速度，为海啸预警系统提供支持.更根本的是，数学科学有助于映射海底的地形，并根据不规则地形布置在相隔数百英里的地方的独立海洋验潮仪的数据推断大尺度波浪的行为.

（7）数学与先进制造

•CAD核心功能建立在计算几何等数学基础上

在数字化设计制造技术发展的每个关头，数学方法都起了关键作用.例如，计算机辅助设计（CAD）的核心功能，曲面造型、参数化设计、协同设计等，直接建立在计算几何、计算代数几何、自动推理、运筹学等数学分支的基础上.

•用于高档数控机床的数控系统

数控系统是数控机床的“大脑”，是决定其性能的关键因素.数控系统的若干核心技术，是实现高速、高精控制的基础.这些问题可以归结为几何计算、非线性方程组求解与最优控制问题.

（8）数学与人工智能

•人工智能归根结底是算法

人工智能实际上是一个将数学、算法理论和工程实践紧密结合的领域，归根结底是算法.也就是数学、概率论、统计学等各种数学理论的体现.例如一个概率公式加上一个马尔可夫假设就可以做到简单的机器翻译和语音识别.

•数学让人工智能成为规范的科学

人工智能综合性很强，机器识别、遗传算法、概率统计、数据科学、数值分析等等都在人工智能领域起着重要的作用.数学是这些分门别类知识的核心基础，数学让人工智能成为了一门规范的科学.

可以说数学不以“有用”为研究的原点，实际上却又是极为“有用”的学科.数学的基础性、引领性使得它在科学研究中处于独一无二的核心地位，它对一个国家、一个民族的长远发展的影响是深远的、至关重要的.长期以来，数学研究在发达国家的科学战略中始终居于最重要的地位.因此，从长远来看，我们的国家要实现可持续发展不能缺少原创性的科学研究，不能缺少原创性的数学研究.目前我国处于创新发展的关键时期，历史机遇难得.为实现中华民族的伟大复兴，亟须更加重视数学的研究与教育，重建对数学的正确认识，希望有更多的优秀人才加入数学研究的队伍当中，探寻发现数学那不止于“有用”的独特魅力.