大学应用数学函数的间断点

函数的不连续点称为该函数的间断点，即不满足函数连续的三个条件之一的点为间断点.由于函数在某一点间断的情况很多，为了区别，通常将间断点进行分类.

定义1.18（间断点的分类）　设x0为函数y=f（x）的间断点.如果左极限f（x0-0）和右极限f（x0+0）都存在，则称x0为函数y=f（x）的第一类间断点；否则，称x0为函数y=f（x）的第二类间断点.对第一类间断点：若f（x0-0）=f（x0+0），则称x0为函数y=f（x）的可去间断点；若f（x0-0）≠f（x0+0），则称x0为函数y=f（x）的跳跃间断点.

例如，函数在点x=0处无定义，且，故x=0是函数的第一类间断点（可去间断点）.因为若补充定义，令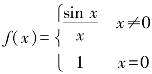，则函数在点x=0处连续.

图1.16

例1.23　讨论函数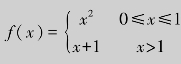在x=1处的连续性.

解　因为函数f（x）在分段点x=1处的左、右极限

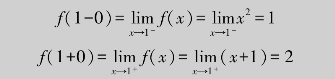
因为左、右极限都存在但不相等，所以x=1是函数f（x）的第一类间断点（跳跃间断点）.如图1.16所示，图像在x=1处出现了跳跃现象.

例1.24　讨论函数在x=0处的连续性.

解　因为函数在x=0处无定义，且在x=0处左、右极限都不存在，所以x=0是y的第二类间断点.又因为当x→0时，函数在-1到1之间作无限次震荡（见图1.17），这样的间断点称为震荡间断点.

图1.17(www.xing528.com)

另外，若，则称x0为y=f（x）的无穷间断点.例如，函数在点x=0处无定义，且，则称x=0是函数的无穷间断点.

练习1.4

1.讨论下列分段函数在分段点处的连续性.若为间断点，判定其类型，并写出连续区间.

2.设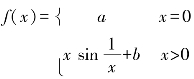，试确定常数a，b的值，使f（x）在点x=0处连续.

3.求下列极限.

4.求下列函数的间断点并判定其类型；如果是可去间断点，则补充定义使函数在该点连续.

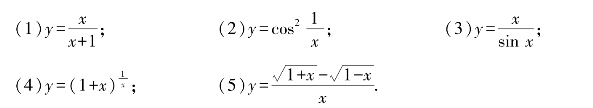
5.证明方程x5-3x=1在（1，2）中至少有一个实根.

6.证明方程x·2x=1至少有一个小于1的正根.

7.设f（x），g（x）在[a，b]上连续，且f（a）＞g（a），f（b）＜g（b），证明：方程f（x）=g（x）在（a，b）内必有实根.