比较无穷小-大学应用数学

前面讨论了两个无穷小的和、差、积仍然是无穷小，而两个无穷小的商不一定是无穷小.商的极限出现几种不同情况，反映了无穷小趋于0的速度的差异.为了比较无穷小趋于0的快慢，引入如下概念.

定义1.14　设α与β是自变量在同一变化过程中的两个无穷小，

（1）如果，则称β是比α高阶的无穷小，记作β=o（α）.

（2）如果，则称β是比α低阶的无穷小.

（3）如果，则称β与α是同阶无穷小.

（4）如果，则称β与α是等价无穷小，记作α～β.

例如，因为，所以当x→0时，x2=o（x），x是比x2低阶的无穷小，5x与x是同阶无穷小，sin x～x.

等价无穷小在求两个无穷小之比的极限时，具有重要的作用，对此有如下定理.

定理1.8　设在自变量的同一变化过程中，α～α′，β～β′，且，则

定理指出，在计算函数极限时，无穷小因子可用其等价无穷小代换，而极限不改变.

可以证明：当x→0时，有如下常见的几个等价无穷小量，应熟记.(www.xing528.com)

例1.18　求下列极限.

解　（1）因为x→0时，tan 5x～5x，sin 3x～3x，所以

（2）因为x→0时，，所以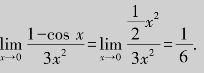

（3）因为x→0时，sin x～x，tan x～x，，所以

必须注意的是：等价无穷小代换只能对分子或分母中的因式进行代换.若极限式中分子或分母中的无穷小是以和或差的形式出现，则不能代换，否则导致错误的结果.

练习1.3

1.求下列极限.

2.求a的值，使函数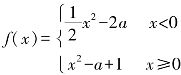在x=0处的极限存在.

3.证明当x→0时，x3+2x2是比x高阶的无穷小.

4.利用等价无穷小的性质，求下列极限.