【摘要】：-y=cot x，当x→0时；y=ex，当x→+∞时；y=ln|x|，当x→0时；，当x→∞时.6.指出下列函数在什么情况下是无穷小，在什么情况下是无穷大?
1.无穷大的定义
定义1.13 在自变量x的某一变化趋势下，若函数的绝对值|f（x）|无限增大，则称函数f（x）为自变量x在该变化趋势下的无穷大量，简称无穷大.f（x）为x→x0的无穷大，记作
例如，当x→1时，
的绝对值无限增大，故
是当x→1时的无穷大，即
；当x→0+时，ln x取负值但其绝对值无限增大，故ln x为x→0+时的负无穷大，即
必须注意的是：（1）无穷大是一个绝对值无限增大的变量，而不是绝对值很大的常量.
（2）无穷大不趋向于任何确定的常数，所以无穷大的极限不存在.
2.无穷大与无穷小的关系
定理1.5 在自变量的同一变化过程中，
（1）若函数f（x）是无穷小，且f（x）≠0，则
是无穷大；
（2）若函数f（x）是无穷大，则
是无穷小.
练习1.2
1.观察下列数列的变化趋势，写出他们的极限.(www.xing528.com)
2.利用函数的图形，求下列极限.
3.设函数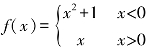
，画出其图像，求极限
，并判定
是否存在.
4.证明
不存在.
5.指出下列各题中，哪些是无穷小，哪些是无穷大?
-
（1）y=cot x，当x→0时； （2）y=ex，当x→+∞时；
（3）y=ln|x|，当x→0时； （4）
，当x→∞时.
6.指出下列函数在什么情况下是无穷小，在什么情况下是无穷大?
7.求下列函数的极限.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
