大学应用数学：初等函数性质与变换

1.基本初等函数

常数函数　　　y=C（C为常数）；

幂函数　　　　y=xa（a为实数）；

指数函数　　　y=ax（a＞0，且a≠1，a为常数）；

对数函数　　　y=logax（a＞0，且a≠1，a为常数）；

三角函数　　　y=sin x，y=cos x，y=tan x，y=cot x，y=sec x，y=csc x；

反三角函数　　y=arcsin x，y=arccos x，y=arctan x，y=arccot x.

以上六类函数统称为基本初等函数.它们的性质、图像见表1.1.

表1.1

续表

续表

2.复合函数

定义1.3　设y=f（u），u=φ（x），且函数u=φ（x）的值域与函数y=f（u）的定义域交集为非空集合，则称y=f[φ（x）]为由y=f（u）与u=φ（x）复合而成的复合函数，其中u叫作中间变量.

必须注意点是：

（1）复合函数的定义可以推广到多个中间变量的情形.

（2）将一个较复杂的函数分解为若干个简单函数时，一定要分清层次，由外到内，逐层分解.

（3）并不是任意两个函数都能构成复合函数.例如，y=arcsin u和u=x2+5就不能构成复合函数.因为当x∈（-∞，+∞）时，u=x2+5≥5，此时y=arcsin u无定义.

例1.5　指出下列函数由哪些简单函数复合而成.

解　（1）可以看作由，u=1+2x复合而成.

（2）可以看作由y=3u，u=v2，v=tan x复合而成.

必须注意的是：能否正确分析复合函数的构成直接决定了是否能熟练掌握微积分的方法和技巧.(www.xing528.com)

3.初等函数

由基本初等函数经过有限次四则运算和有限次函数复合所构成的，并且可以用一个解析式表示的函数，称为初等函数.例如f（x）=x sin x，，f（x）=e5x+1sin x，等都是初等函数；但分段函数一般不是初等函数，如函数不能用一个解析式表示，故不是初等函数.

练习1.1

1.填空题.

（1）若函数，则f（-1）=__________，f（2）=__________，f（0）=________.

（2）若函数，则函数f（x）的定义域为________.

（3）函数的定义域是________.

（4）设，那么f（x）=________.

（5）设f（x-1）=x2-x+1，则f（x）=________.

2.选择题.

（1）已知函数，则f[f（x）]=________.

（2）下列函数中，有界的函数是________.

（3）如果函数y=f（x）的定义域为（0，1]，则函数y=f（2x）的定义域为________.

（A）[0，1]　　（B）[-1，0]　　（C）（0，+∞）　　（D）（-∞，0]

3.下列各组函数是否是相同的函数?

4.试作出函数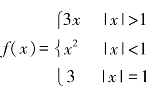的图像.

5.判断下列函数的奇偶性.

6.将下列函数分解为简单函数.