大学应用数学-函数性质详解

1.函数的概念

定义1.1　设x和y是两个变量，D是给定的非空数集，如果变量x在D内任取一个确定的数值时，变量y按照一定的法则f都有确定的数值与之对应，则称变量y是变量x的函数，记作

y=f（x），x∈D，

其中变量x称为自变量，变量y称为因变量（或函数），数集D称为函数的定义域，f称为函数的对应法则.

如果自变量x在定义域D内任取一个确定的数值时，只有唯一的函数值与之对应，则称该函数为单值函数；否则，如果有多个函数值与之对应，则称该函数为多值函数.如y=x2是单值函数；而x2+y2=4是多值函数.如果没有特别说明，本书所讨论的函数都是单值函数.

当x取确定数值x0∈D时，通过法则f，函数有唯一确定的值y0与之相对应，称y0为函数y=f（x）在x0处的函数值，记作

由全体函数值构成的集合称为函数的值域，记作M，即M={y|y=f（x），x∈D}.

由函数的定义知，函数是由定义域和对应法则确定的，因此把函数的对应法则和定义域称为函数的两个要素.若两个函数具有相同的定义域和对应法则，则称他们是相同的.函数的表示方法常用的有三种：表格法、图像法、解析式法.

例1.1　设，求f（2），，f[f（x）].

解　分别用2，，f（x）代替中的x，得

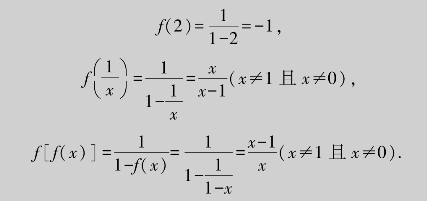
例1.2　下列各组函数是否相同，为什么?

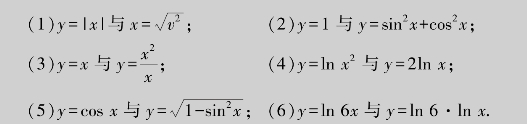
解　因为（1）与（2）中两函数的两要素分别相同，所以是相同的函数；（3）与（4）中两函数的定义域不同，所以是不同的函数；（5）与（6）中两函数的对应法则不同，所以是不同的函数.

2.函数的定义域

函数的定义域通常分为以下两种情况：

（1）对于实际问题，根据问题的实际意义确定.

例如，自由落体运动过程中位移s（t）随时间t变化的函数关系为，定义域为[0，T]，其中T为落地时间；圆面积S是圆半径r的函数S=πr2，定义域为（0，+∞）.

（2）由解析式表示的函数，其定义域就是使表达式有意义的一切实数组成的集合.

例1.3　求函数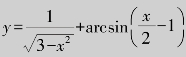的定义域.

解　要使函数有意义，必须有

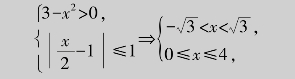
即0≤x＜.因此，所给函数的定义域为[0，）.

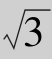3.函数的几种特性

设函数y=f（x）在区间I上有定义（区间I为函数f（x）的整个定义域或其定义域的一部分），则函数一般具有下列几种特性.

（1）有界性.如果存在正数M，使对任意的x∈I，恒有|f（x）|≤M，则称函数y=f（x）在区间I上有界，否则称f（x）在区间I上无界.

从图形上看，有界函数的图像介于两条直线y=-M与y=M之间（见图1.1）.

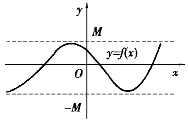
图1.1

例如，函数y=sin x在（-∞，+∞）上有界，因为对任意的x∈（-∞，+∞），恒有|sin x|≤1，而函数在区间（0，1）内无界，但在区间（1，2）内有界.

必须注意的是：讨论函数的有界性，必须先指明自变量x所在的区间.(www.xing528.com)

（2）单调性.若对任意的x1，x2∈I，当x1＜x2时，恒有f（x1）＜f（x2）（或f（x1）＞f（x2）），则称函数y=f（x）在区间I上单调增加（或单调减少）.区间I称为单调增区间（或单调减区间）；单调增加函数和单调减少函数统称为单调函数；单调增区间和单调减区间统称为单调区间.

一般地，单调增加函数的图像为沿x轴正向单调上升的曲线，如图1.2所示；单调减少函数的图像为沿x轴正向单调下降的曲线，如图1.3所示.

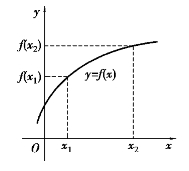
图1.2

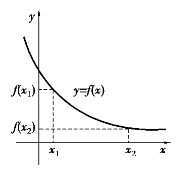
图1.3

例如，y=x3在（-∞，+∞）内是单调增加函数；y=x2在（-∞，0]内单调减少，在[0，+∞）内单调增加，在（-∞，+∞）内y=x2不是单调函数.

必须注意的是：讨论函数的单调性，必须先指明自变量x所在的区间.

（3）奇偶性.设函数f（x）的定义区间I关于原点对称，若对任意的x∈I，都有f（-x）=f（x），则称函数f（x）是区间I上的偶函数；若对任意的x∈I，都有f（-x）=-f（x），则称函数f（x）是区间I上的奇函数；若函数既不是奇函数也不是偶函数，则称为非奇非偶函数.

偶函数f（x）的图像关于y轴对称（见图1.4）；奇函数的图像关于原点对称（图1.5）.

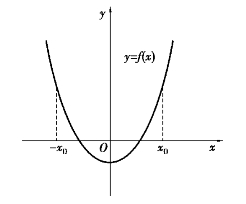
图1.4

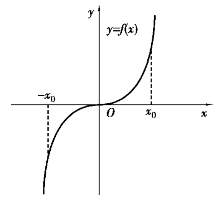
图1.5

例如，y=sin x为奇函数；y=cos x为偶函数；而y=x2+x为非奇非偶函数.

（4）周期性.如果存在不为零的实数T，使得对于任意的x∈I，x+T∈I，都有f（x+T）=f（x），则称函数y=f（x）是周期函数，T是y=f（x）的一个周期.通常所说的周期函数的周期是指它的最小正周期.

例如，y=cos x是以2π为周期的周期函数；y=tan x是以π为周期的周期函数.

4.分段函数

在定义域的不同范围具有不同的表达式的函数称为分段函数，其定义域为各部分定义域的并集.分段函数是整个定义域上的一个函数，不能理解为多个函数.一般来说，分段函数需要分段求值，分段作图，分段表示.

例1.4　王先生到郊外去观景，以2 km/h的速度匀速步行1 h后，他发现一骑车人的自行车坏了，便花了1 h帮人把车修好，随后加快速度，以3 km/h的速度匀速步行1 h后到达终点，然后立即以匀速折返，耗时2 h返回到出发点.请把王先生离家的距离关于时间的函数用图像法描绘出来.

解　王先生离家的距离y（km）是时间x（h）的函数，图形如图1.6所示.用解析式法表示为

该函数为分段函数，其函数定义域为[0，5].

5.反函数

定义1.2　设函数y=f（x）的定义域为D，值域为M.如果对于M中的每个数y，在D中都有唯一确定x与之对应，且使y=f（x）成立，则确定了一个以y为自变量，x为因变量的函数，称为函数y=f（x）的反函数，记作x=f-1（y），其定义域为M.值域为D.

由于习惯上用x表示自变量，用y表示因变量，因此将反函数中x与y互换位置，即记作y=f-1（x），x∈M，并称函数y=f-1（x）是函数y=f（x）的反函数.函数y=f（x）与其反函数y=f-1（x）的图像关于直线y=x对称（图1.7）.

必须注意的是：只有单调函数才有反函数，且其反函数也是单调函数.

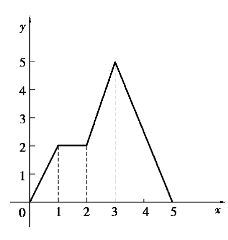
图1.6

图1.7