智能运输系统中轨道区间段干扰问题解决方法

发生事故、故障或者遭到破坏之后，当然也可能是由于维护的原因，某段轨道可能暂时无法使用。虽然RYNSORD并没有在设计过程中就制定出处理这种问题的办法，但是本章假设：一旦发生故障，轨道区间段的两个端点上的车站在一个时间步长内，即实际操作的60s内就知道了该故障的发生。此外，故障发生时正行驶在某轨道区间段上的火车将继续行驶，并安全到达另一端。在端点的车站将通过取消所有预留来阻止其他火车使用该轨道，并强制命令所有受影响的火车重新选择路径。

图7.6 8条链路出现故障，时间步长为1440、输入率为0.05时每列火车的误差标准Ⅰ与车辆 进入时间的函数（图a）以及每列火车的误差标准Ⅱ和仿真时间的函数（图b）

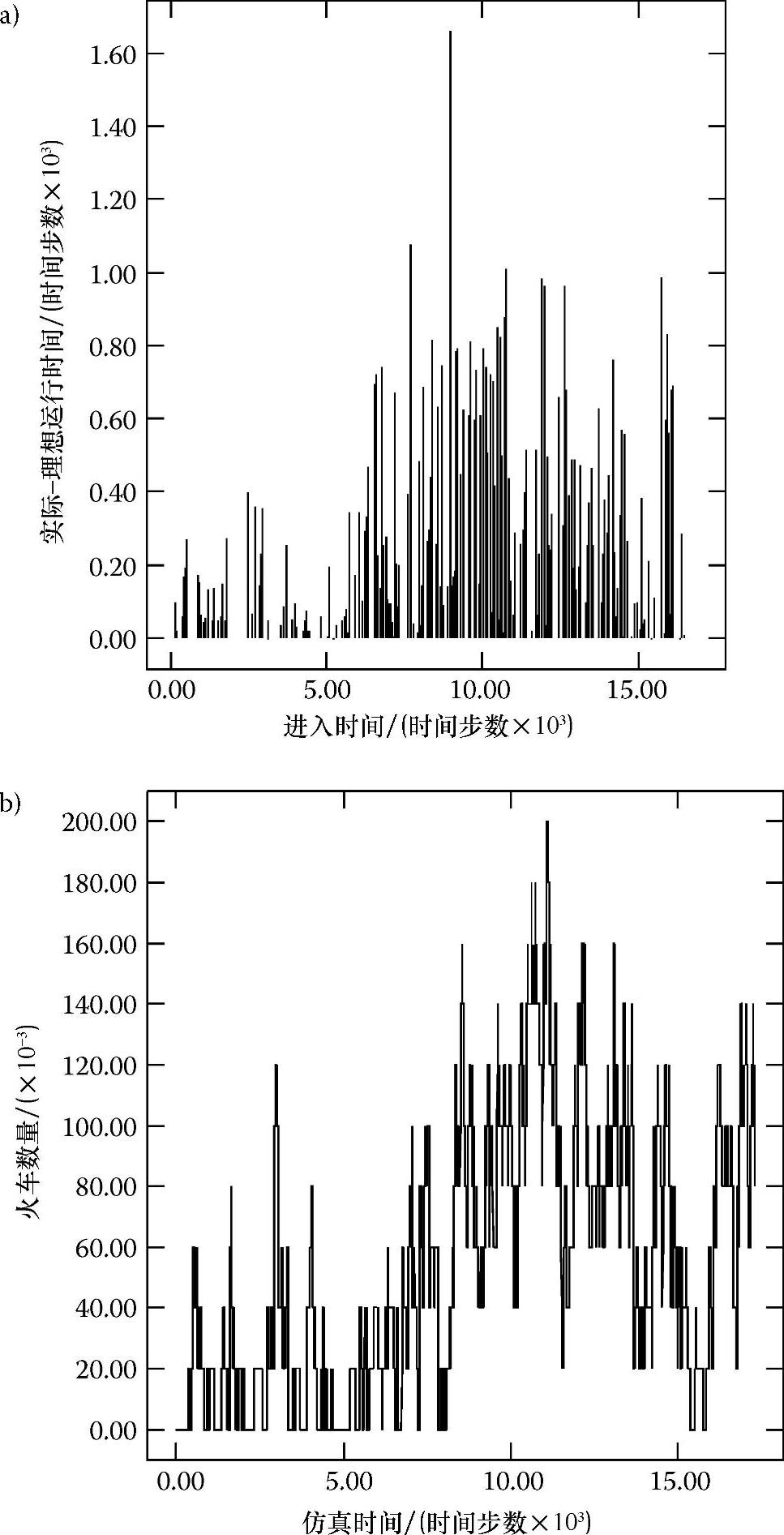
图7.78 条链路出现永久故障，输入率为0.05时每列火车的误差标准Ⅰ随进入时间变化的函数（图a）以及每列火车的误差标准Ⅱ随仿真时间变化的函数（图b）

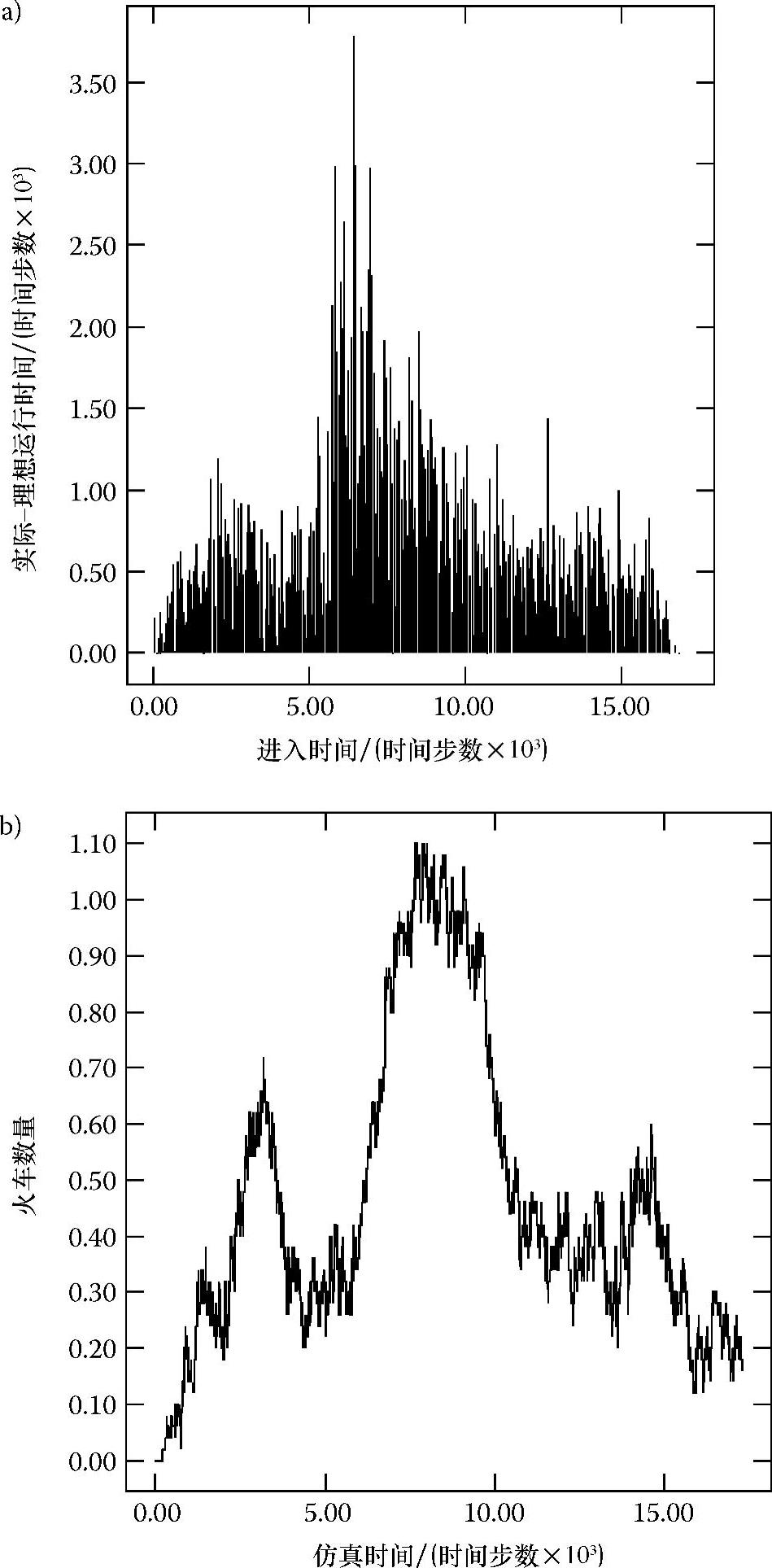
图7.8 8条链路出现故障，时间步长为1440、输入率为0.125时每列火车的误差标准Ⅰ随进入时间变化的函数（图a）以及每列火车的误差标准Ⅱ随仿真时间变化的函数（图b）

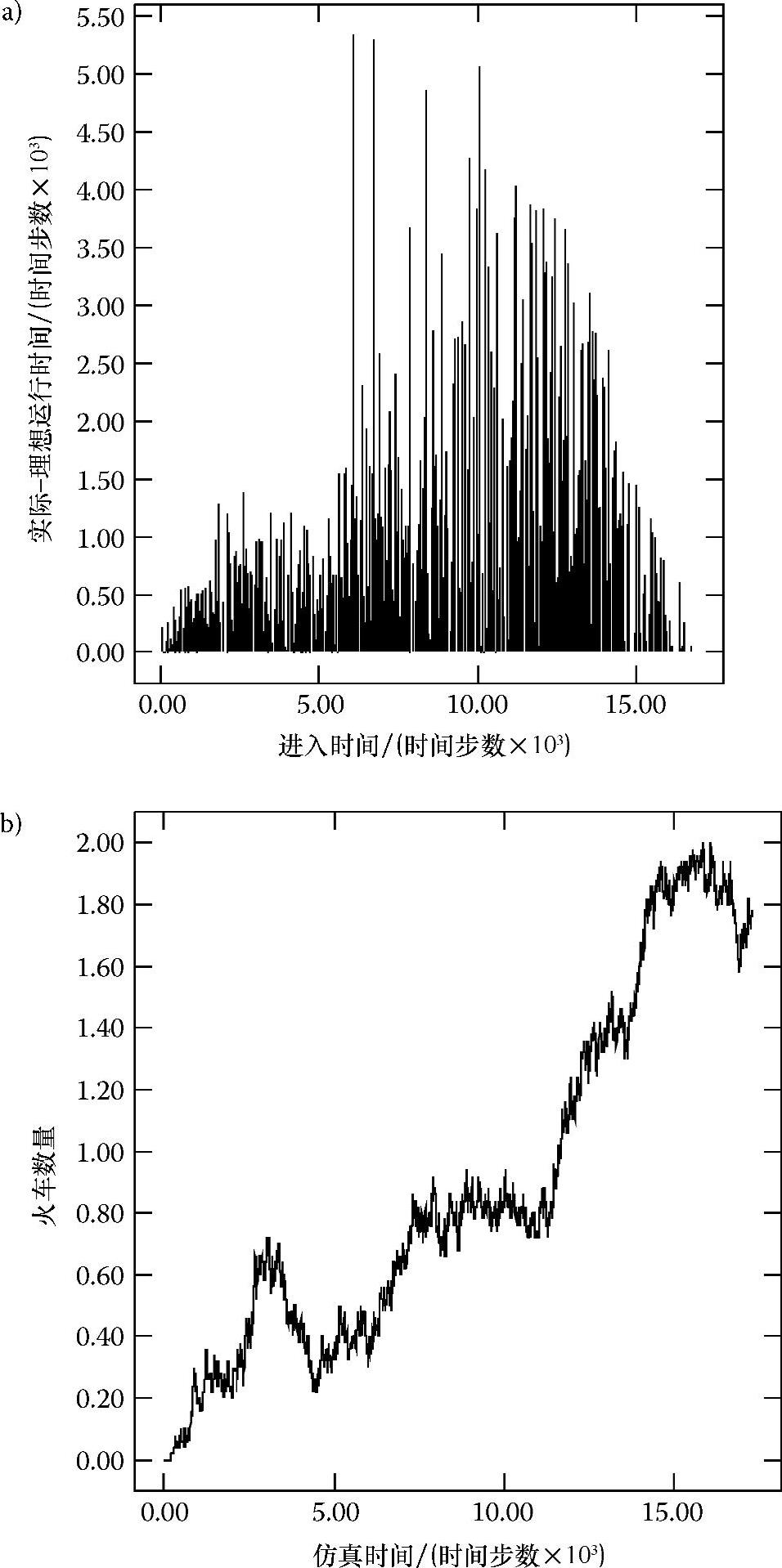
图7.9 8条链路出现永久故障，输入率为0.125时每列火车的误差标准Ⅰ随进入时间变化的函数（图a）以及每列火车的误差标准Ⅱ随仿真时间变化的函数（图b）

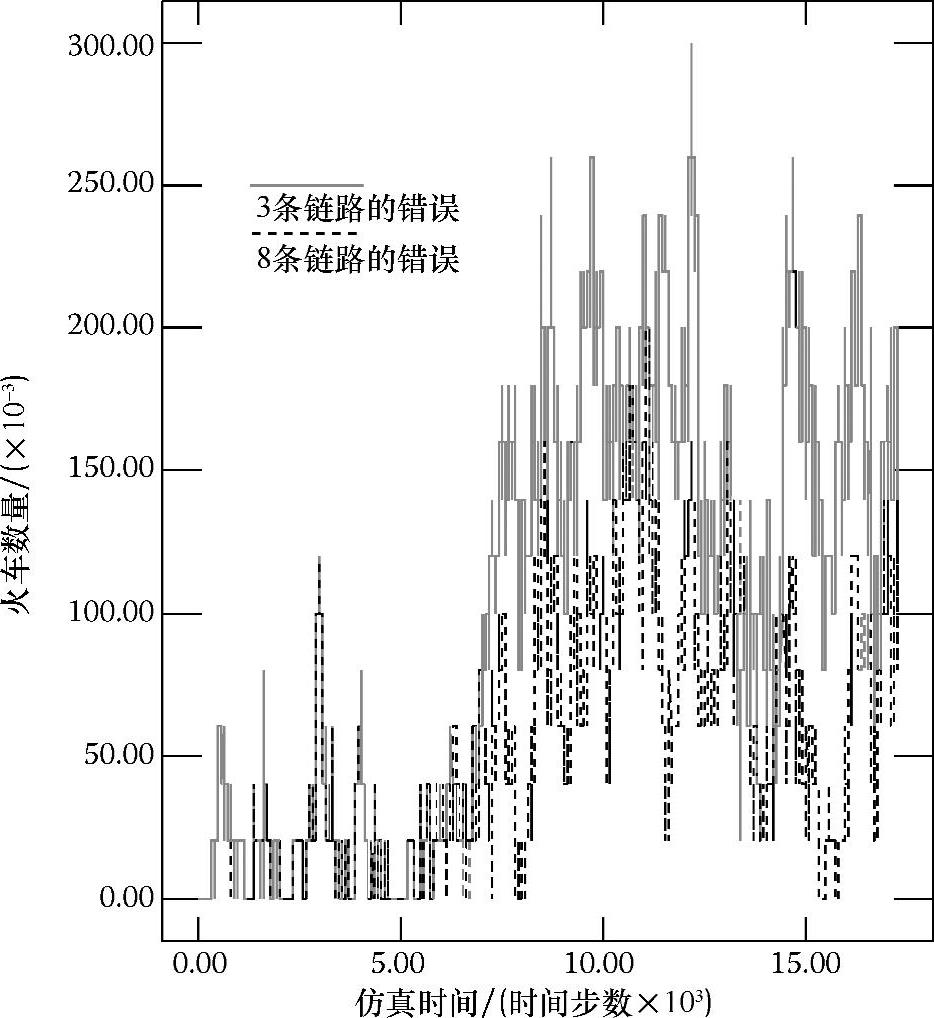
图7.10 输入率为0.05的情况下，分别有3条和8条链路永久 失效时，每列火车的误差标准Ⅱ随仿真时间变化的情况

虽然轨道故障对火车产生的影响看起来与通信链路故障的影响类似，但是实际却有很大不同。图7.11a和图7.11b都是整个网络的一部分。图7.11a说明了夏洛特维尔（35）和里士满（36）之间的一个通信链路故障的情况，而图7.11b显示的则是夏洛特维尔（35）和里士满（36）之间的轨道故障情况。考虑一列火车在通信链路出现故障之前的某个时间，从罗阿诺克（48）进入系统，终点站是里士满。当链路正常时，预留请求得到答复，火车会选择其请求的路线A。无论此时的通信链路情况如何，火车在夏洛特维尔和里士满之间的轨道区间段上正常行驶是可以保证的。相反，在图7.11b中，火车启动后，轨道发生故障，火车到达夏洛特维尔时，轨道仍未修复。此时火车被迫重新选择一条新的路径，甚至在通过帕克斯堡到达里士满之前，可能需要返回到林奇堡。这个例子似乎说明轨道故障可能会极大影响RYNSORD的性能，但接下来的分析将证明通信故障的影响可能更加严重。(www.xing528.com)

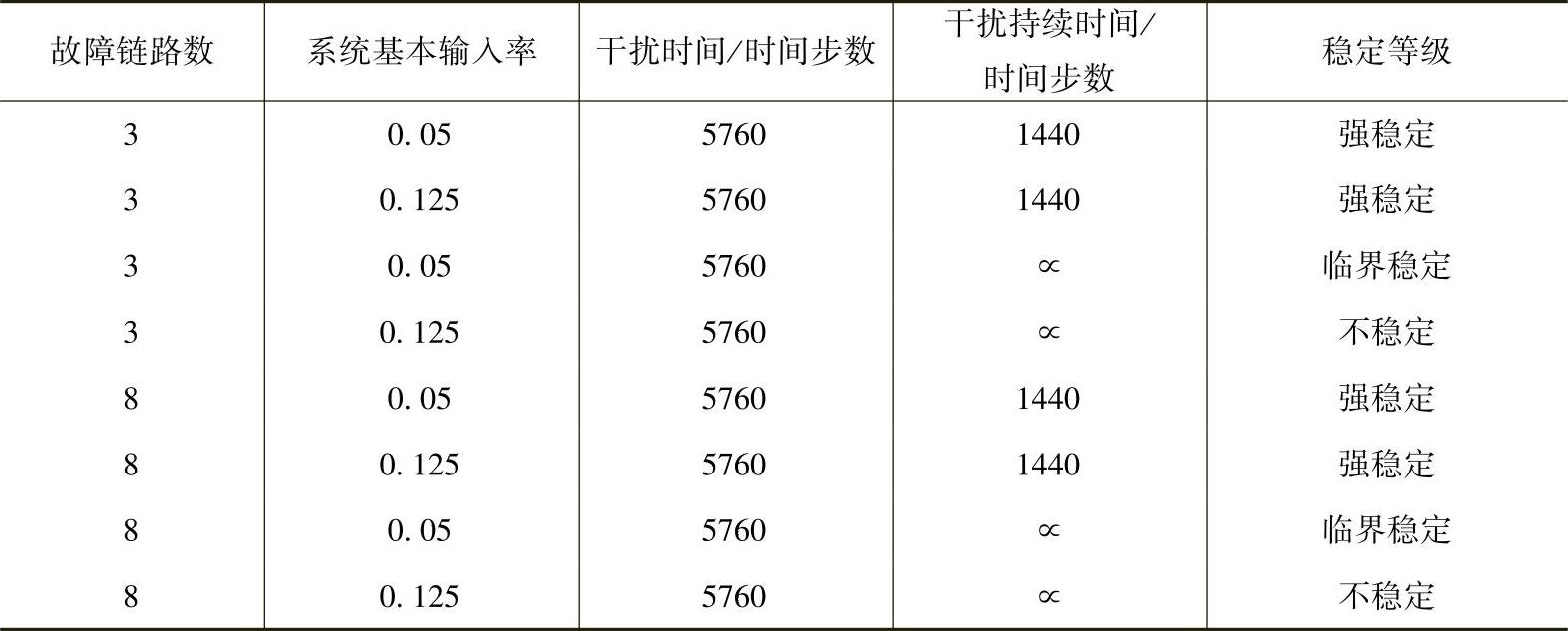
我们设计了一个试验，其中轨道如本章之前所描述的情况一样：有2个分别由3条和8条轨道区间段组成的集合发生了故障，分别对应于由3条和8条通信链路组成的集合发生故障。表7.4所示轨道发生故障时的性能表现与通信受到干扰时的性能表现（见表7.3）完全一致。除了某些关键因素不同外，误差标准图也非常类似于通信干扰的情况。图7.12a描述了在高流量输入率下，8条链路（或轨道）的集合发生故障，且故障持续时间为有限的1440个时间步长时，通信链路故障和相应的轨道故障的误差标准Ⅱ变化情况。虽然RYNSORD在这两种干扰情况下都是强稳定的，图7.12a中两条曲线变化也非常类似，但还是可以看出通信干扰的误差幅度明显高于轨道干扰。图7.12b则显示在低流量输入率下，8条链路（或轨道）集合发生永久性故障的情况下，误差标准Ⅱ的变化情况。虽然在两种情况下，RYN-SORD都是临界稳定的，且图形的变化也是极为相似的，但是同样可以看到通信干扰对应的误差幅度远远高于轨道干扰。一种可能的解释是：对于一列火车而言，只有当故障轨道真正无法被一列火车使用时，通信链路的故障才会真正影响到火车竞争预留的能力，从而影响到火车使用轨道的能力。

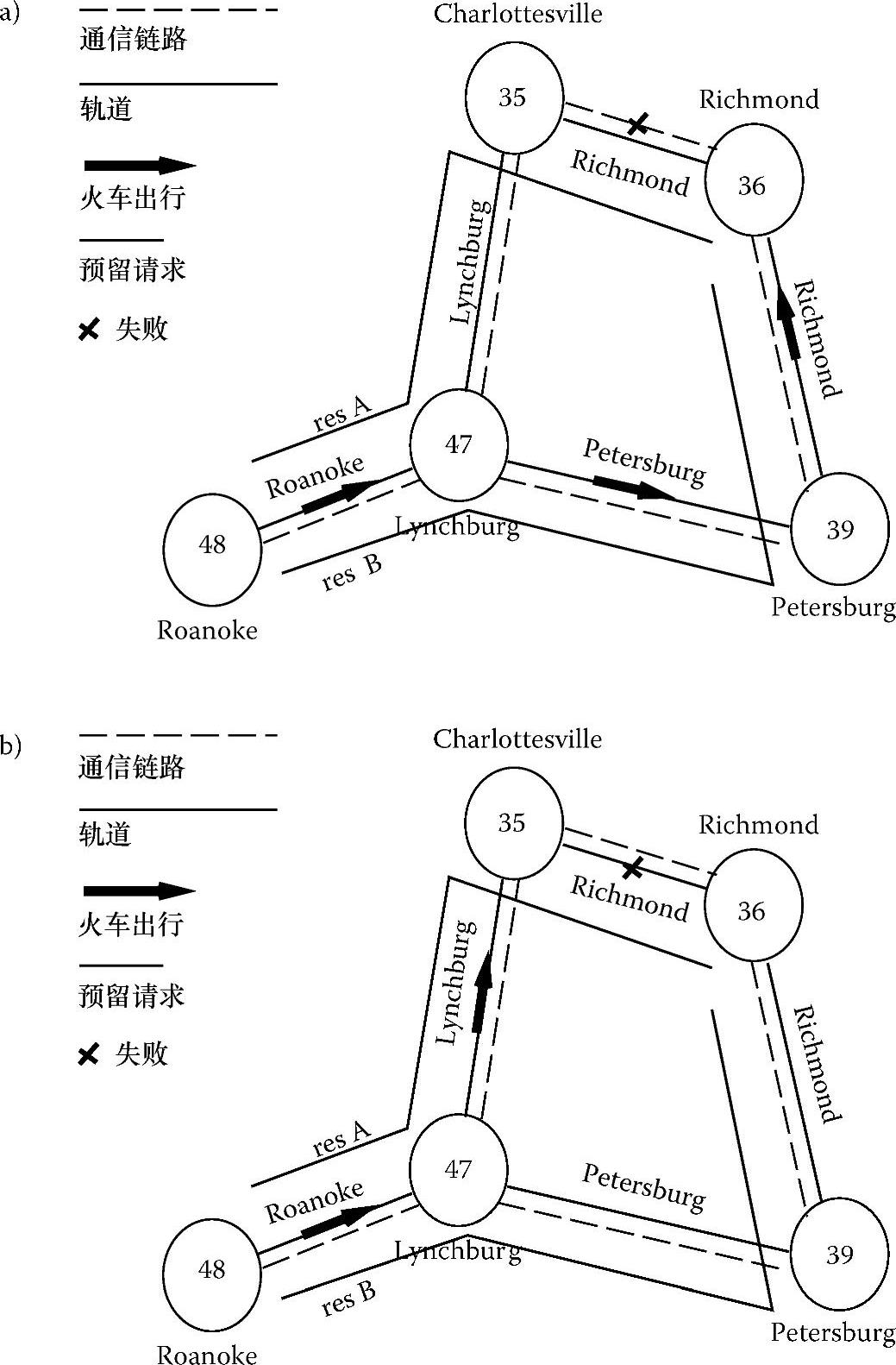
图7.11 通信链路故障的影响（图a）以及轨道区间段故障的影响（图b）

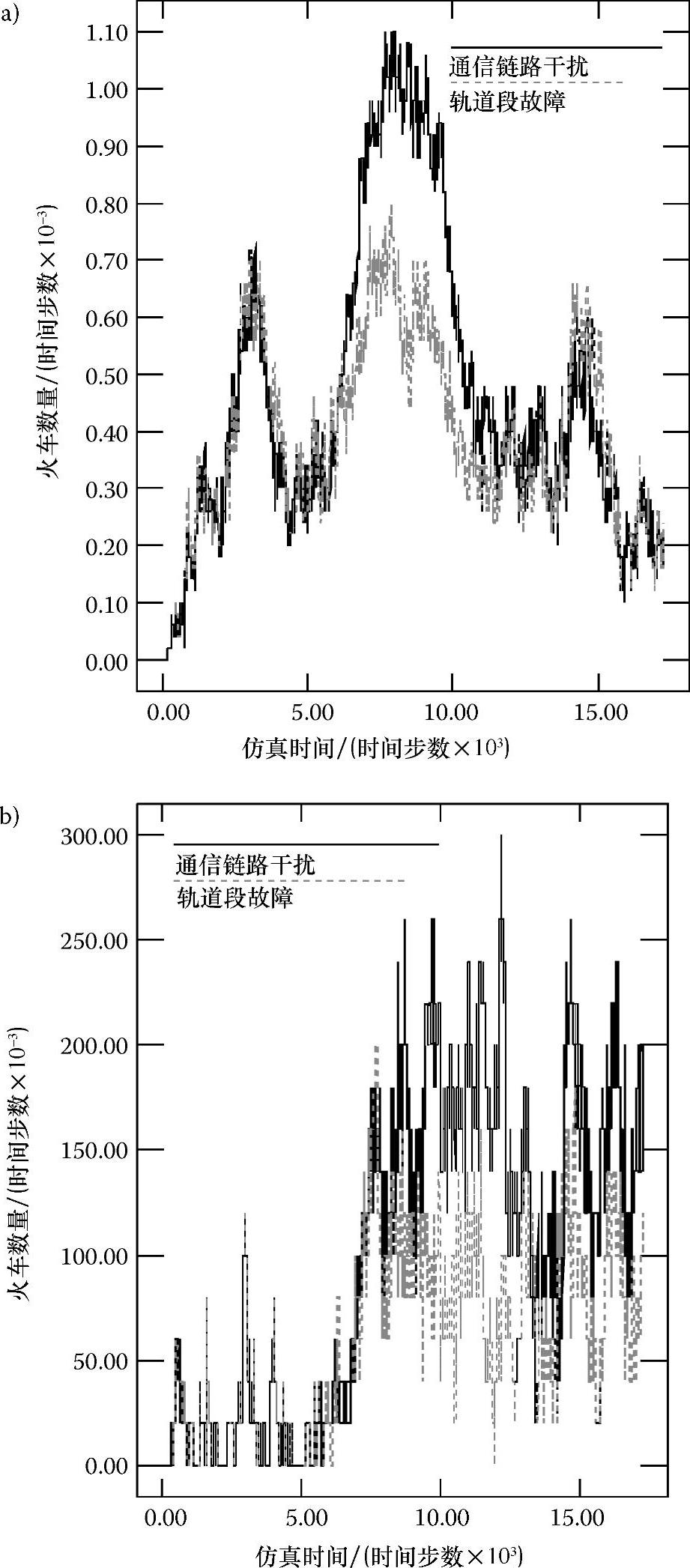
图7.12 误差标准Ⅱ在通信链路干扰和轨道干扰情况下随仿真时间变化的情况

a）高输入率和有限干扰时间 b）低输入率和永久性干扰

表7.4 轨道干扰情况下的性能结果

研究的局限性

RYNSORD的稳定性分析表明：在面对时间有限的流量输入率干扰和轨道区间段故障干扰时，它是强稳定的。而在遇到永久性干扰时，稳定性的判断取决于干扰开始之前的流量输入率。然而，在遇到通信链路故障时，RYNSORD的稳定性表现较差，这部分的算法需要重新进行设计以提高抗干扰的能力。