车站和火车通信干扰问题调查及解决措施

车站之间和火车与车站之间的互动是RYNSORD中最关键的通信任务，没有这些，火车就不能成功地预留轨道，也不能朝着它们的目的地行驶。为满足正确性的要求，除非火车关于某段轨道的预留请求已被明确批准，否则火车不能在该段轨道上行驶。如果一列火车起动的预留请求还在等待回答，火车绝不能尝试使用请求中的轨道。因此，这里有意引入干扰影响预留过程，但是不会影响RYNSORD的正确性。

这些干扰的特征为：消息从一个站传到另一个站的过程中永远不会到达目的地。此外，车站与火车之间的通信也不会到达接收器。如果发生这种情况，RYNSORD中的火车会做出如下行为：当一列火车没有收到对于它的预留请求的答复时，它会选择使用可用的备用路径，而不是无限期地等待回应。如果它的两个预留请求都没有收到回应，火车会暂时改变它的前向值并重新发出预留请求。火车传送预留请求的两条通信链路都不通，这种情况几乎是不可能发生的，火车最近的活动会确保得到至少一个预留回应。而一旦这件不可能的事情发生了，火车会在车站等待，并且在下个时间步长根据重设的前向值重新开始它的预留请求。一般来说，计算机通信故障通常都是比较短暂的，本文推想等待一个时间步长是合理的，在这个时间内通信链路可能就恢复了，而火车不用着急地去迂回绕路。人们还认识到两个车站之间的通信故障并没有对于轨道区间本身的用途造成破坏，该故障仅仅影响到那些想通过不是该轨道控制者的车站实现预留的火车，因为信息永远不会到达该轨道的控制车站，它才是唯一有能力批准预留的车站，从控制该轨道的车站驶出的火车才可以请求并使用该轨道。

许多实验可用于测试稳定性：各种不同的通信链路故障、选择不同的故障持续时间直至永久性故障或使用不同的流量输入率值等，其目的都是分析通信干扰对RYNSORD的影响，并确定使RYNSORD在干扰下能保持稳定的流量输入率。在第一个试验中，两组分别由3条和8条链路组成的集合分别出现故障，这些链路依次通过其两端的车站来识别。如果有一条链路是将某车站和网络其他部分相连的唯一通信线路，就要特别小心，避免它出现故障。3条链路以上的组合称为高流量链路，选择8条链路的组合说明我们期望考虑故障在整个网络上分布的情况。仿真时间为17280个时间步长，分别以0.05和0.125作为稳态输入率。故障在时间步长为5760时引入，持续时间为1440个时间步长。因此t_pert=5760，而t_{pert_end}=5760+1440=7200。选择故障持续时间为1440个时间步长，是因为它相当于一整天的实际操作时间，也提供了足够的维修时间。在另一组试验中，通信链路出现永久故障，即t_pert=5760，t_{pert_end}=∞。

3条链路的集合包括巴尔的摩（34）、华盛顿（33）、底特律（9）、托莱多（10）、罗阿诺克（48）和林奇堡（47）。

8条链路的集合包括克里夫兰（11）、哥伦布（12）、罗切斯特（27）、锡拉丘兹（28）、圣路易斯（5）、底特律（9）、威尔森（40）、罗利（41）、夏洛特维尔（35）、里士满（36）、纽约（31）、费城（25）、诺克斯维尔（18）、布里斯托尔（20）、帕克斯堡（44）和亨廷顿（45）。(www.xing528.com)

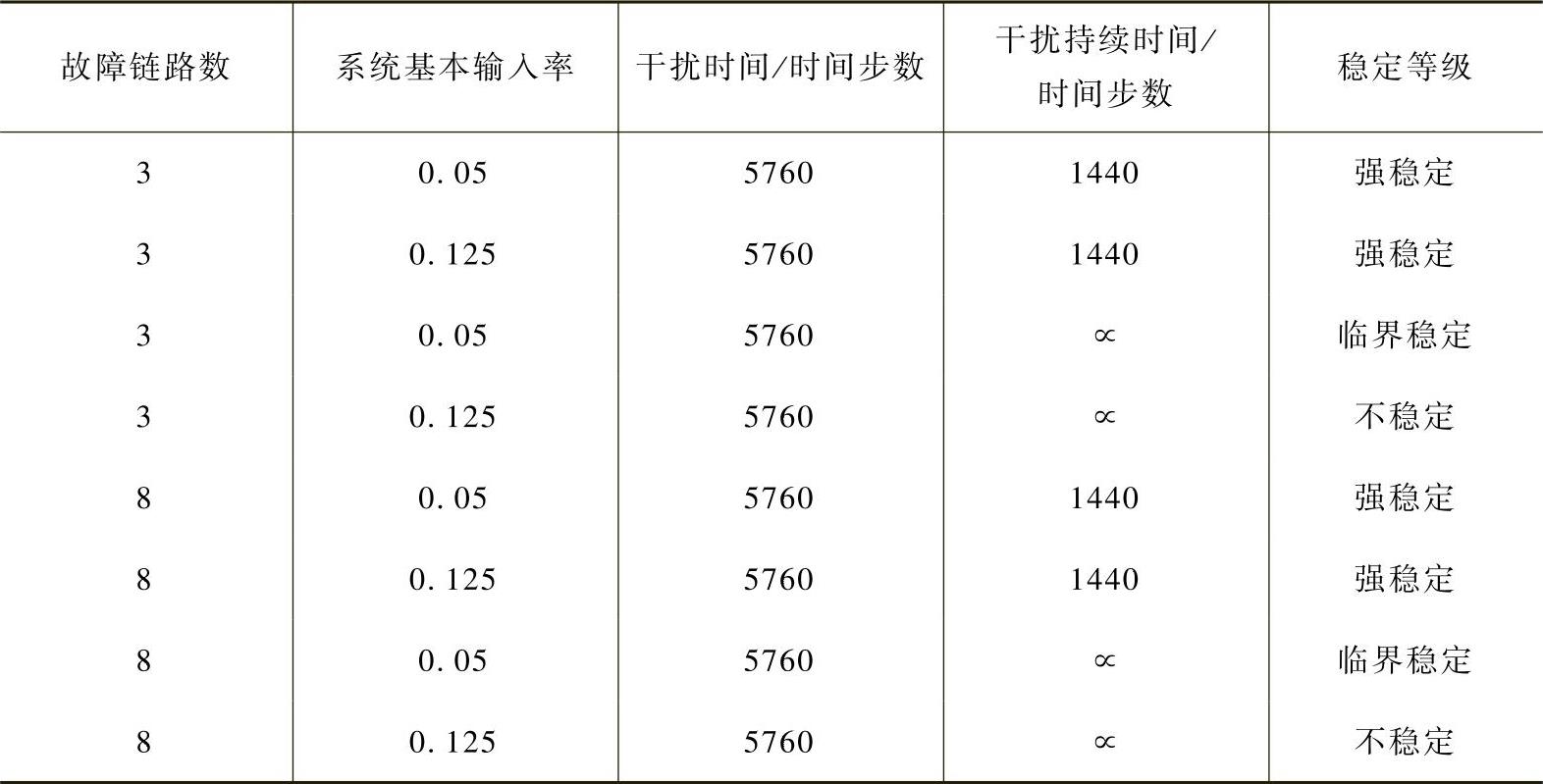
表7.3总结了RYNSORD的性能表现结果，并证明了就有限时间的故障而言，RYNSORD是强稳定的。由于通信故障能被快速修复，所以仿真结果是令人满意的。不过，对于在两种链路集合中存在的永久性干扰，在流量输入率为0.05和0.125时，RYNSORD分别表现为临界稳定和不稳定。显然，临界稳定和不稳定的临界值是流量输入率、轨道故障数量和具体的轨道故障的函数。图7.6 a～图7.9b是8条故障轨道集合的情况，显示了在不同的流量输入率和干扰持续时间下的误差标准Ⅰ和Ⅱ的变化情况。有人指出误差标准Ⅱ映射了误差标准Ⅰ的行为，3条故障轨道集合的结果与8条轨道集合的结果类似，在这里不作论述。

表7.3 通信干扰下的性能表现

然而，对两种故障轨道集合的误差标准Ⅱ进行对比分析的结果（见图7.10）揭示了下列情况：图7.10中的数据对应于较低的流量输入率和永久性故障。虽然两种情况下RYNSORD都是临界稳定的，但3条链路故障集合的最终稳态点更糟糕，即相对于8条链路故障的集合，其误差临界值更大。结果表明，具体的链路故障原因（如拥挤的程度）比出现故障的链路数量更重要。此外，仿真终止后进行的离线分析结果表明，使用一个或以上的3条链路组合的火车总数为201列，这些链路被用在它们的最短路线上。相反，只有167列火车会利用一个或以上的8条链路集合。因此，稳定分析可能有助于找出那些即使出现故障，也可能不会影响RYN-SORD性能的通信链路。