与任何现实世界系统一样,RYNSORD是为了在稳定状态中运行而设计的,但在运行时可能会遭遇不可预测的情况,例如输入率的快速波动等。因此,最常见的对RYNSORD中输入率的干扰通常包括输入率在很短的时间段内突增等。随着输入率增长幅度和干扰持续时间的增加,对RYNSORD中稳态工作点的选择很可能会影响其稳定性。人们期望能将RYNSORD设计成一个强稳定系统,即随着干扰的终止,在有限的时间内,最终至少能返回到原始稳定状态的系统。许多实验都是根据不同的初始稳态工作点设计和进行的,它们都能在不同的干扰情况下,达到一次RYNSORD系统的稳态点。然后,才会随着仿真的进展和分析去衡量误差准则Ⅰ和Ⅱ。
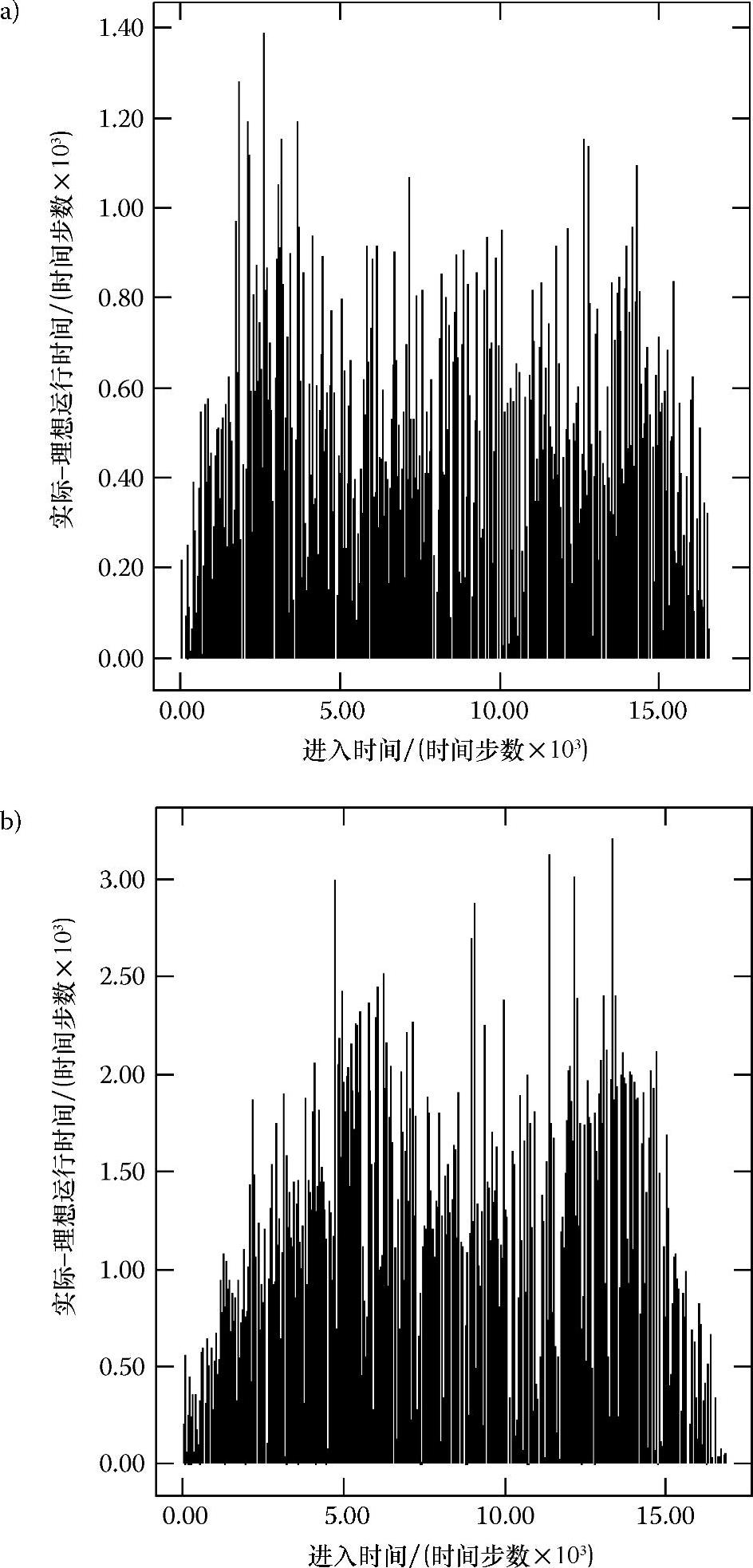
图7.2 不同输入率情况下每列火车的误差标准Ⅰ和火车进入时间的函数关系
a)输入率=0.125 b)输入率=0.14
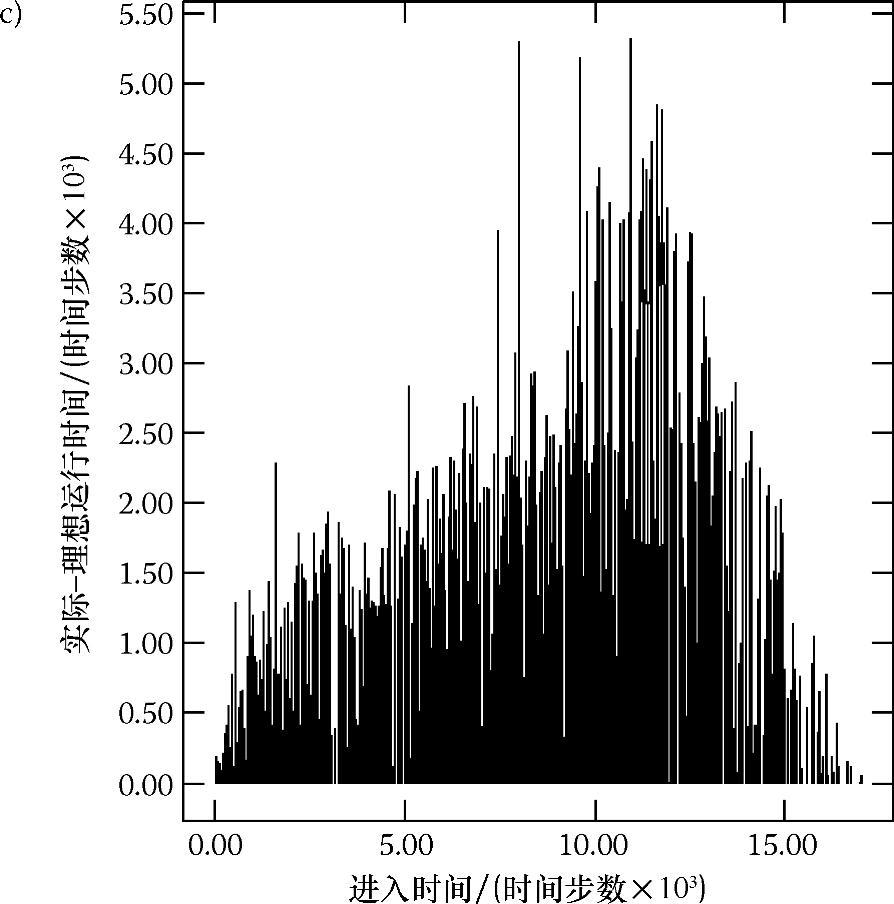
图7.2 不同输入率情况下每列火车的误差标准Ⅰ和火车进入时间的函数关系(续)
c)输入率=0.175
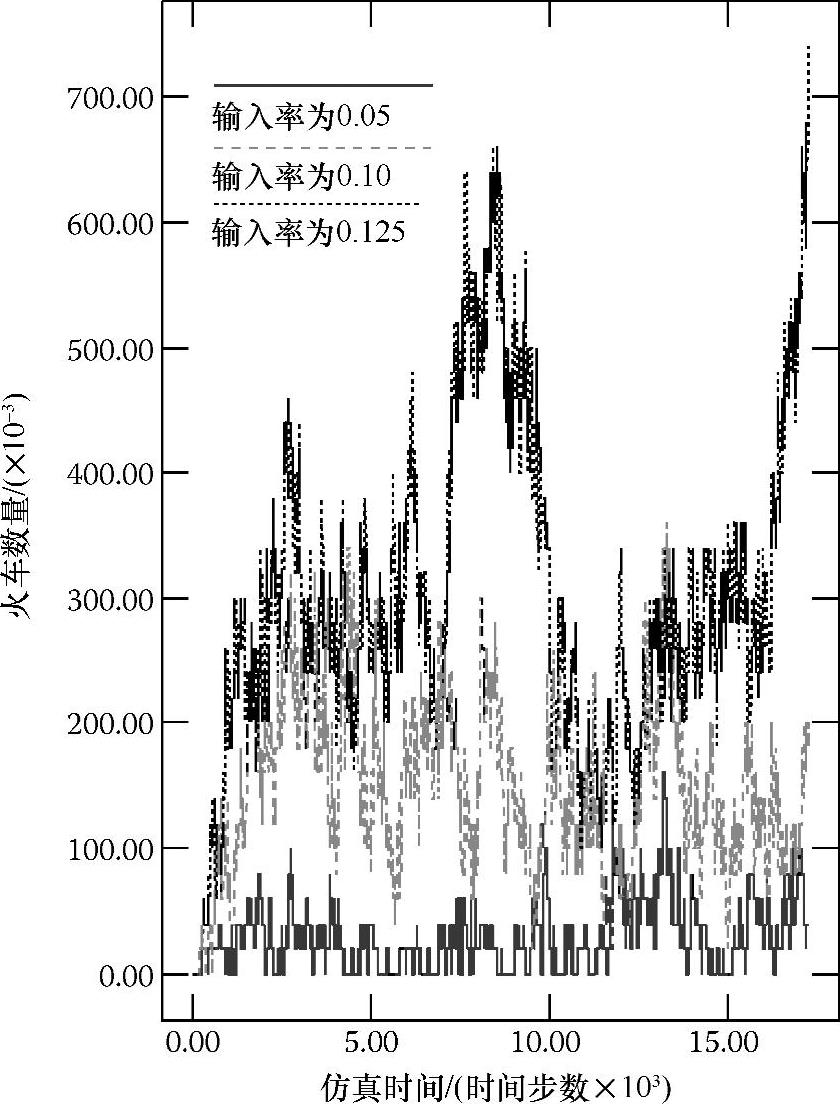
图7.3 不同稳态输入率下误差标准Ⅱ与仿真时间的函数关系
表7.2总结了三种不同的输入率干扰下的系统特性。这三个干扰的幅度设计的目的是要使RYNSORD成功超过稳态点。在图7.4a~c中,分别对应于三种情况,把每列火车的误差标准Ⅰ作为它进入系统时间的一个函数。图7.5描述了三种情况下的误差标准Ⅱ与仿真时间之间的函数关系。图7.4a和图7.5中所有的误差标准都随着干扰的出现而即时增加。然而,随着时间的推移,所有三种情况中的误差幅度都会下降,而RYNSORD最终都返回到初始的稳态点,因此,RYNSORD就输入干扰而言是强稳定的。
表7.2 对输入率的干扰和系统特性(https://www.xing528.com)
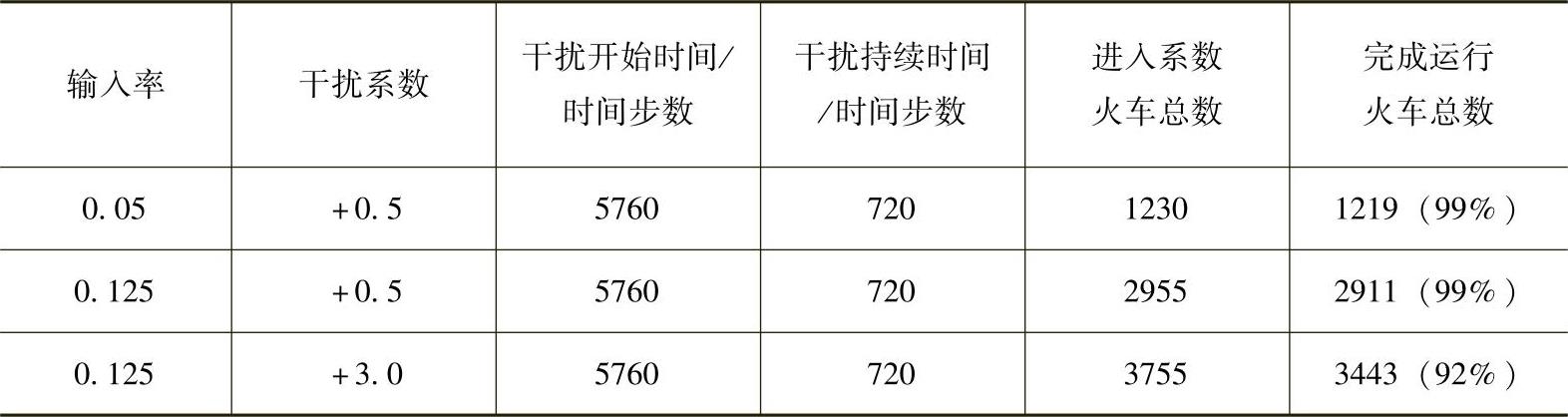
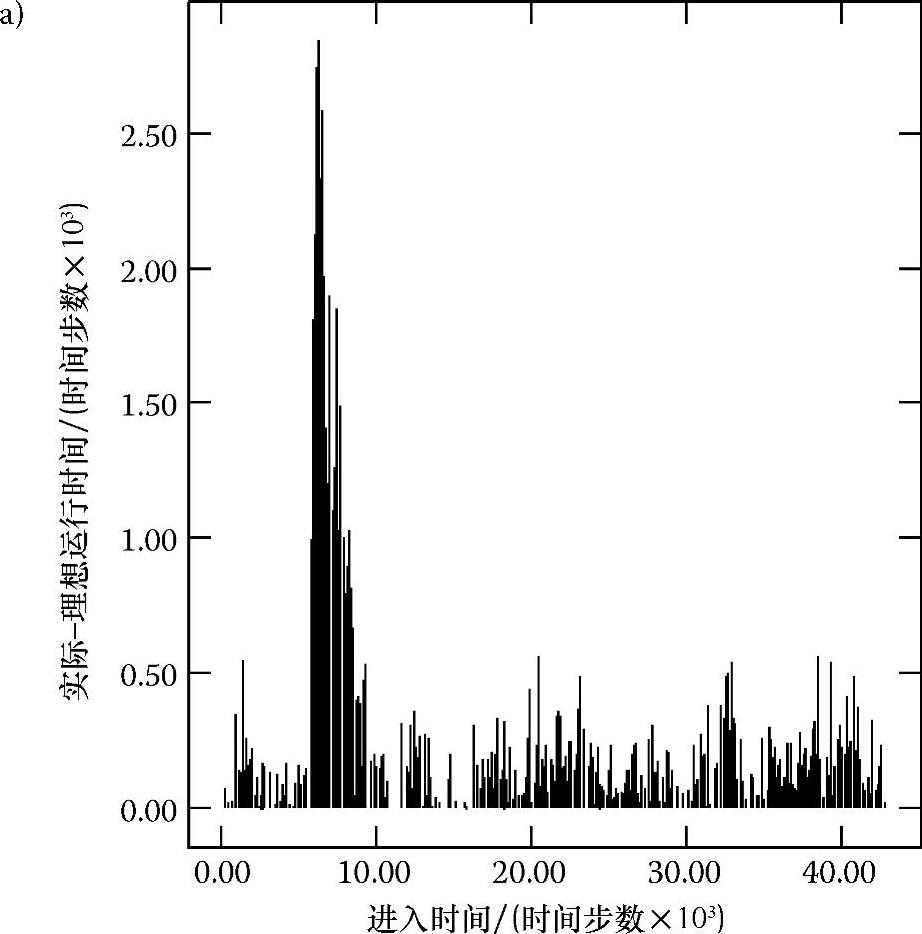
图7.4 每列火车的误差标准Ⅰ随火车进入时间变化的函数关系
a)输入率为0.05,干扰系数为0.5
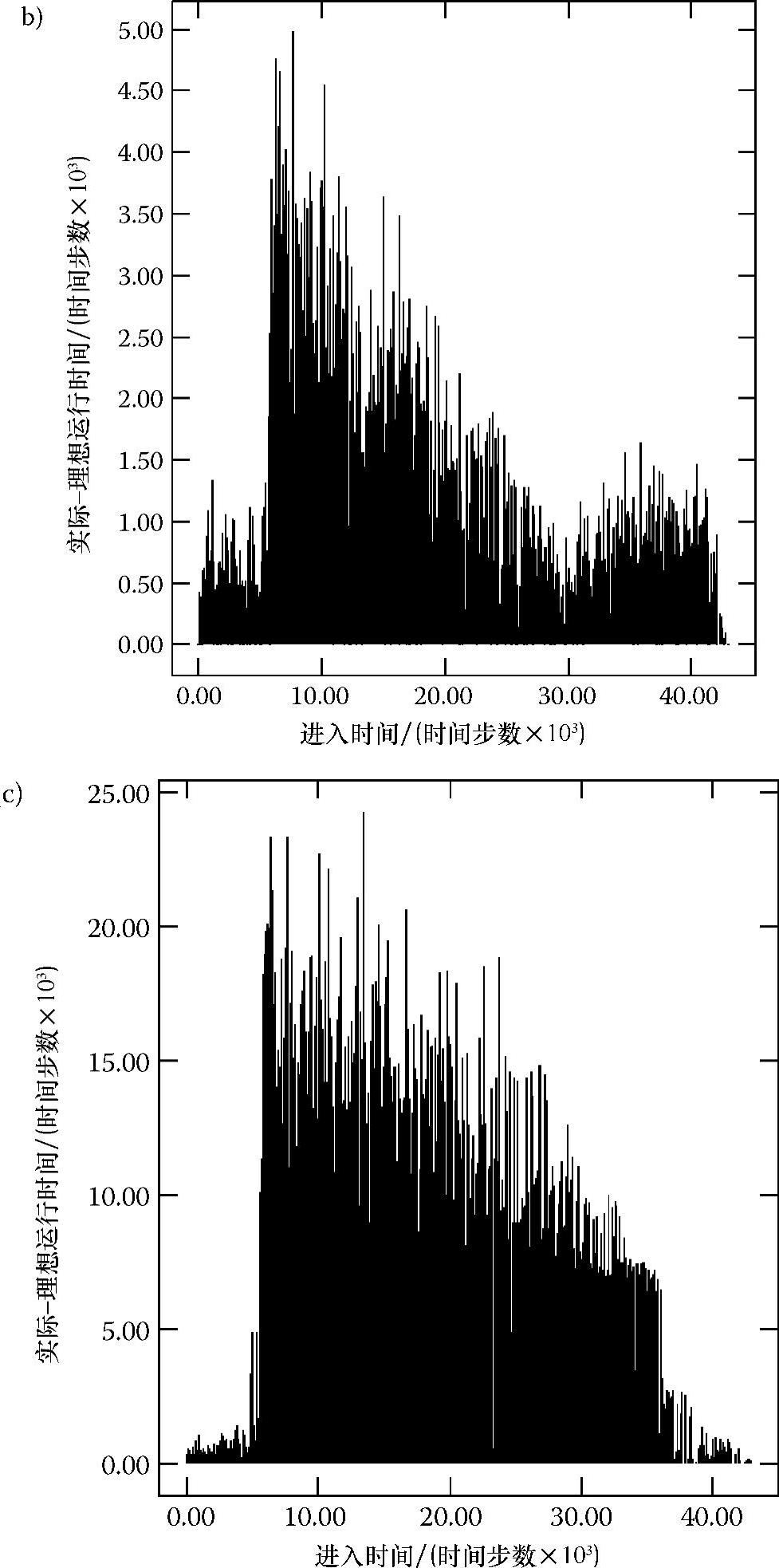
图7.4 每列火车的误差标准Ⅰ随火车进入时间变化的函数关系(续)
b)输入率为0.125,干扰系数为0.5 c)输入率为0.125,干扰系数为3.0
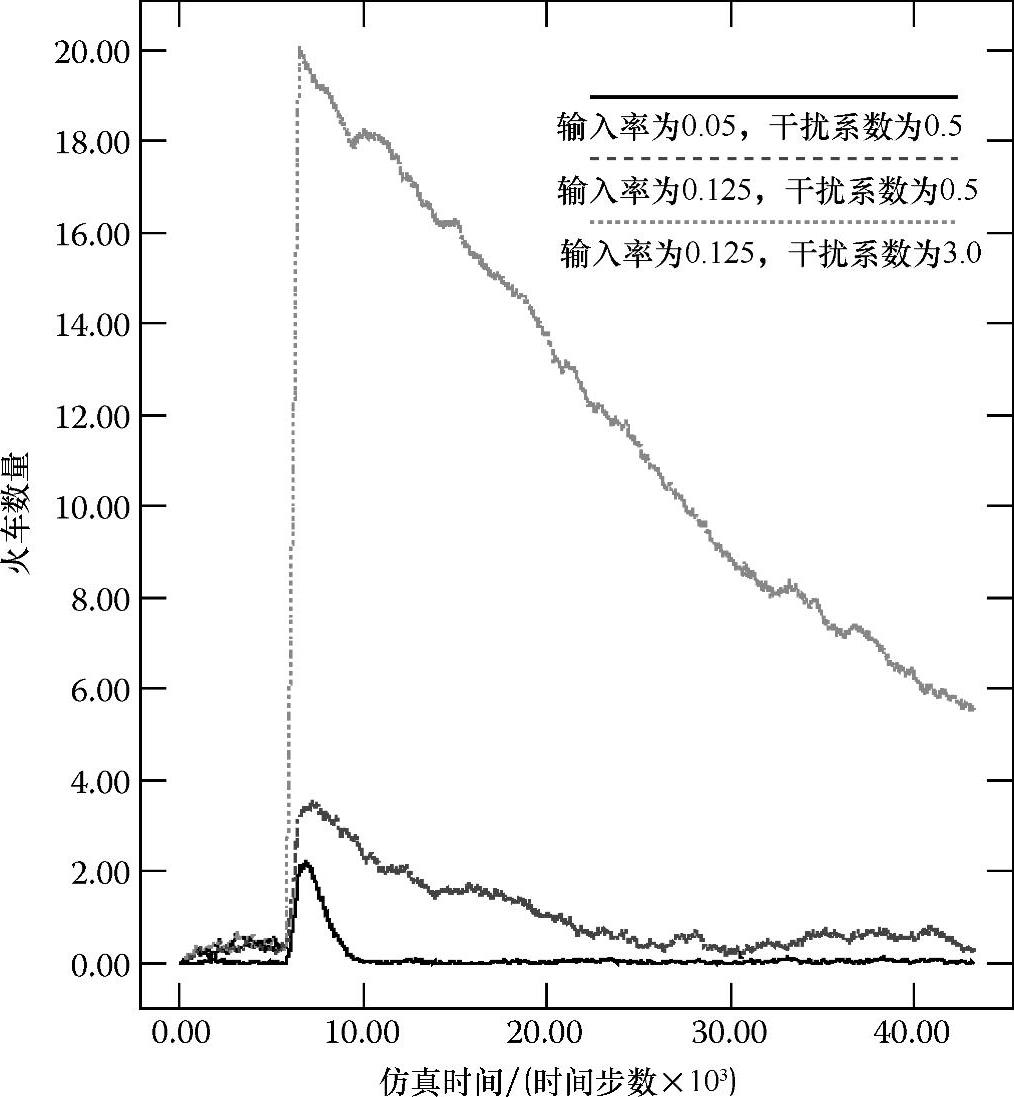
图7.5 误差标准Ⅱ在不同输入干扰下随仿真时间变化的函数关系
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




