智能运输系统第2版：绿色结构设计性能分析

DICAF要达到的目标包括：①所有车辆都能快速到达目的地；②能高效利用包括高速公路路段区间在内的所有资源。此外，DICAF还要建立一个可扩展、实用而经济的系统，该系统对每个DTMC的通信和计算需求都非常小。进一步来说，对于某个给定的高速公路系统以及在一定时间段内真实的交通分布而言，DICAF中任何一对起讫点之间的任意车辆所需出行时间一定是一致的，并与车辆在该时间段出现的时间无关。

为了对DICAF的性能表现作系统阐述，本章中首先定义了几个独立参数以及主要的性能评价指标，并根据各种典型的交通条件进行了大量的仿真实验，如图6.1和图6.9的两个高速公路系统所示。图6.1的高速公路系统包含9个DTMC和12个路段；图6.9包含50个DTMC和85个路段。每个DTMC控制它东边和南边的路段。假设所有路段长都是10mile，车速是随机确定的（后面再详细说明）。

独立参数包括①进入系统的车辆数；②车辆输入密度，即车辆被输入DICAF中的频率；③车速的分布。

主要性能评价指标包括：①到达终点的车辆出行时间分布；②到达终点的车辆比例；③出行时间的均值和标准差，它是交通密度的函数；④选定路段的C.M.值分布，它是仿真时间的函数；⑤不同交通密度下各路段C.M.值的平均值；⑥个体车辆的出行时间，是它们进入DICAF时间的函数；⑦在每条路段上的车辆平均数。上述指标分别对应不同的车辆输入密度。除此之外，还有两种方法可以更好地检查DICAF在车辆出行时间最短方面的性能表现：第一种⑧是每辆车在出行过程中实际平均车速的分布，它与期望速度相关。第二种评价方法的目的则是为了能帮助我们更好地理解期望车速的分布对DICAF的影响，这可以通过测量在μ值较高、σ值相同以及μ值较高、σ值较小两种情况下车辆的平均出行时间而获得。这两种情况下的车辆平均出行时间被分别称为评价指标⑨和⑩。

为了预测DICAF分配整个通信任务的结果，下面定义另外两个性能指标，包括：⑾每个DTMC到车辆的最大数据传送率；⑿泛洪消息总数的分布，接收发送均由DTMC负责，是仿真时间的函数。泛洪消息是来自其他DTMC的，带有其他路段C.M.值信息。

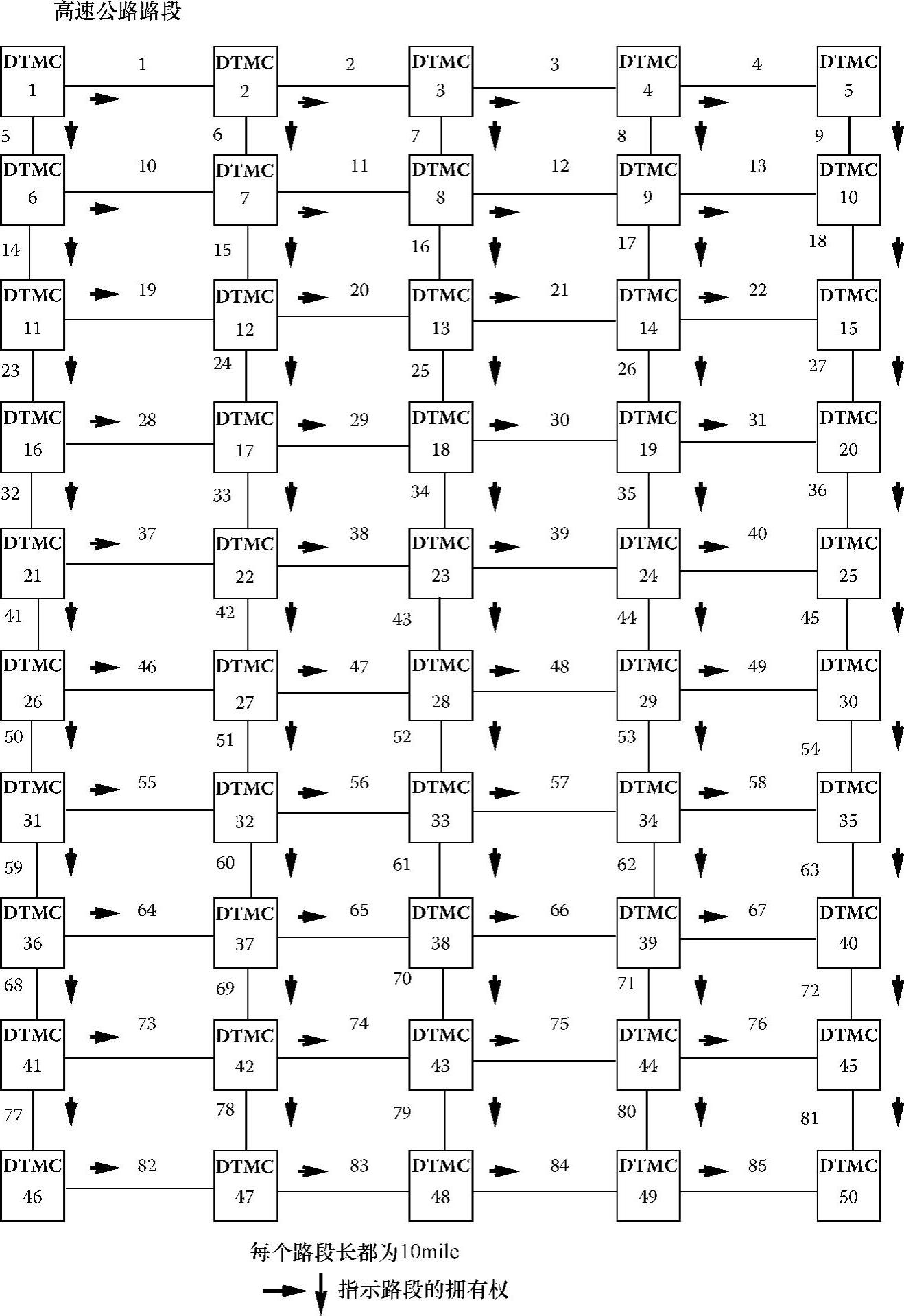
图6.9 DICAF模拟的第二个典型高速公路系统

在DICAF中，车辆通过一个数据结构来表示，并以电子速度，而不是较低的实际车速，从一个DTMC传递到另一个DTMC。因此，DICAF仿真能够比实际路段上车辆的运行快很多倍，这就使我们能在许多有代表性的情况下对DICAF的表现进行详细研究。DICAF在设计上比实际路段运行快90倍，就意味着仿真1s相当于实际路段运行90s，24h路段实际运行就只需要（24×60×60÷90）s=960s（16min）的仿真时间。这在DICAF中是以下列方式实现的：车辆从之前的DTMC到达现在的DTMC仅需几毫秒。然而，车辆到达终点DTMC后会有意延迟一段时间，延迟的时间值等于实际高速公路上的行驶时间除以90，这样就能保证模拟的准确性，保证DICAF中对与仿真方案有关的每辆车出行特性表达的精确性。

平均车辆长度假定为0.0025mile，根据式（6.1），可以知道任意路段上允许的车辆最大数量为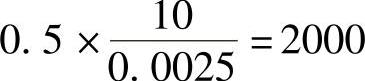辆。输入交通分布采用随机函数来产生DICAF中所有出现在DTMC处的车辆。每次仿真运行都相当于实际路段一天24h的运行。据此，交通发生器在每次仿真过程中产生的车辆数相当于实际路段一天24h的车辆数。在每个DTMC中，会给每辆产生的车辆随机分配一个终点DTMC。在整个仿真过程中，进入任一DTMC处的车辆数都是时间的一个非单值函数。而车辆速度则是利用drand48伪随机发生器函数随机产生的，并以特定的μ和σ值服从正态分布。每辆车都被赋予一个唯一标识符，对于一个拥有9个DTMC的高速公路系统来说，标识符按如下方法计算：（DTMC标识符×10000）+（1…DTMC处产生的最大车辆数）。对于一个拥有50个DTMC的高速公路系统而言，标识符按如下方法计算：（DTMC标识符×1000000）+（1…DTMC处产生的最大车辆数）。路段允许的最大C.M.值是100mile/h，允许的最高和最低车速分别是90mile/h和30mile/h。因此，在本章中，图6.1和图6.9显示的高速公路系统的大部分性能表现结果都是在μ=50mile/h、σ=10mile/h的条件下获得的。此外，图6.1中的公路系统在DICAF中对两种情形进行了仿真：①μ=65mile/h，σ=10mile/h；②μ=65mile/h，σ=5mile/h。图6.1中的高速公路系统要求有10个处理器并行、异步地进行处理，而图6.9中的高速公路系统则要求有51个SUN Sparc10同时运行。输入DICAF中的车辆数由交通密度函数控制，假设在图6.1中其取值分别为3、6和8。交通密度值D表示由每个DTMC中随机产生的，在仿真运行的每一秒钟内进入DICAF的车辆数，其范围为0～D。可以知道与密度取值3、6、8相应的车辆数分别是8528、21572和30284。

RIDOT会根据24h内每个路段上的实际最大车辆数来确定主要高速公路的交通密度数据，这些高速公路包括I-95、I-195和I-295等。由于同一车辆可能行驶在不同的路段上，所以非常有必要根据交通密度地图^[89]来估算进入整个罗德岛高速公路系统的车辆总数。我们注意到，3车道的I-95高速公路承载了最多交通流量，24h最大流量达到了约89302辆。也就是说单车道路段上最大的24h标准交通流量接近30000辆。罗德岛是一个非常小的州，面积仅为40×16mile²（1mile²=2.58999×10⁶ m²），却拥有I-95这条至关重要的道路，因此本章假定I-95是所有行驶在罗德岛高速公路路段的车辆的必经之路。于是，进入罗德岛高速公路系统的最大车辆数将达到30000辆/天，也即DICAF中最高交通密度8所代表的实际交通情况。

在图6.9所示的50个DTMC的高速公路系统中，进入DICAF中的车辆总数是45296，对应交通密度为3，仿真速度也比实际运行速度快90倍。

这里要注意，每辆车的产生都是随机的，即车辆的来源、目的地以及速度等都是随机变量。当产生并仿真的车辆数超过45000辆时，就可以认为所得到的结果能合理地、公正地评价DICAF的性能。我们进行了超过400次的仿真，尽管每次都有不同的种子值，但可以看到数据的一般行为大体相似，所以我们在这里只针对一次特定的仿真运行结果进行报告。还要注意，μ值和σ值都不会被测量，而是不失一般性地由假设获得。μ的置信区间是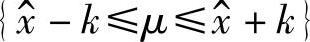。其中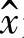，是计算平均值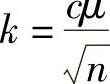；，c与置信水平γ有关；σ是测量方差；n是样本数量。本章中，n超过45000意味着k值很小，即置信区间很小，即使是对较大的c值也一样，这说明具有较高的置信水平。

这个部分展示的性能表现数据，是根据每秒的仿真样本中的关键指标获得的。

图6.10展示的就是一个包含9个DTMC的高速公路系统在交通密度分别为3、6和8的情况下车辆期望速度的正态分布。X轴表示车辆速度，从30mile/h到90mile/h；Y轴表示各种期望速度下的车辆数。显然绝大部分车辆希望行驶速度在55mile/h左右，几乎没有车辆希望以更高或更低的速度行驶。

为了对DICAF与传统的TMC方案的性能进行对比，一般认为需要开发一个采用集中调度的仿真器，并在单处理器上依次操作。在本研究中，没有开发这种单处理机仿真器的原因有以下两个：第一，要表示超过30000辆车的数据结构需要非常庞大的存储空间；第二，仿真器的执行速度有可能会非常低。在本章中，我们提出了一种评价DICAF绝对表现的方法：对于每辆车而言，完成出行的时间是按照从起点DTMC到终点DTMC的最短路径长度（mile）除以车辆的期望速度来计算的。这个时间就是理想出行时间，因为只有当DICAF中仅有一辆车行驶，而没有其他车辆和它争夺资源的情况下才能实现。从绝对意义上来讲，一辆车的理想出行时间是它所能达到的最佳状态。当一次仿真运行完成时，每辆车所需要的实际出行时间是根据车辆从起点驶向各自终点的过程中车辆采集到的信息而获得的。对于车辆而言，实际出行时间是仿真过程中车辆出行路径上所经过的每个DTMC对之间行驶时间的累计和。某辆车的出行时间差别率这样计算：（车辆实际出行时间-理想出行时间）/（理想出行时间）×100%。根据定义，每辆车的出行时间差别率必须是正值，即大于或等于0，并能反映车辆的出行时间超出绝对极小值的程度。图6.11a～c分别表示在密度为3、6、8的情形下，每辆车的出行时间差别率。X轴表示唯一的车辆标识符，范围从10000到90000。平均值和标准差在密度为3、6、8的情形下分别是{1.89%，6.09%}，{1.85%，5.71%}，{2.12%，6.14%}。所有车辆出行时间差别率的平均值从1.89%增加到2.12%，反映了由于有更多的车辆在路段上行驶而导致所有车辆总出行时间的增长。进一步来说，即使DICAF系统里有超过30000辆车，车辆的平均出行时间也仅比最佳时间高2.12%。此外，最坏情况下的车辆平均出行时间，如图6.11c所示，也仅比最佳时间高85%，也就是比理想出行时间的两倍稍低。

图6.10 在交通密度为3、6和8的情况下车辆期望速度的正态分布

显然，这些发现证明了DICAF具有良好的性能。因此，尽管高速路段上有30284辆车行驶，但DICAF中每辆车的自主分布式的动态路径选择结果却与理想情况十分接近。曲线图揭示了以下原因：在并行处理研究中，人们普遍认为分布式算法能更快得到结果，而从集中式算法中得到的解却是开放性的解。在分布式算法中，当地的实体在执行决策的过程中，只能连接系统的一小部分。虽然人们很担心不能连接系统全部内容可能会有问题，但DICAF的结果却显示其效果非常好。也就是说，可以证明，在某些情形下，DICAF中运用分布式算法能在快速求解的同时得到高质量的解。据此，作者提出了一种从问题的集中描述中提取分布式算法的新的数学框架^[90]。

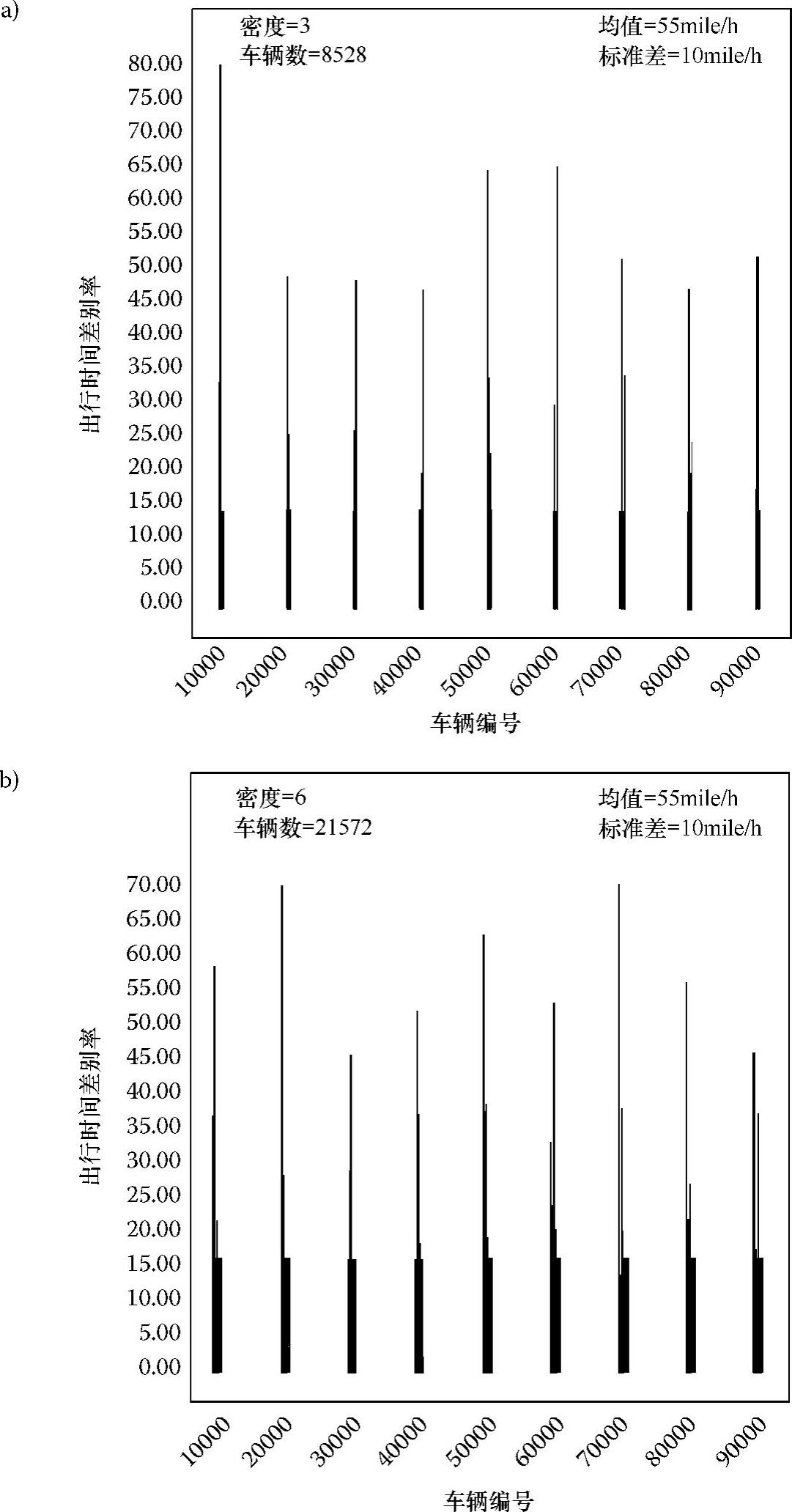
图6.11 在密度为3、6、8的情形下，所有车辆的出行时间差别率

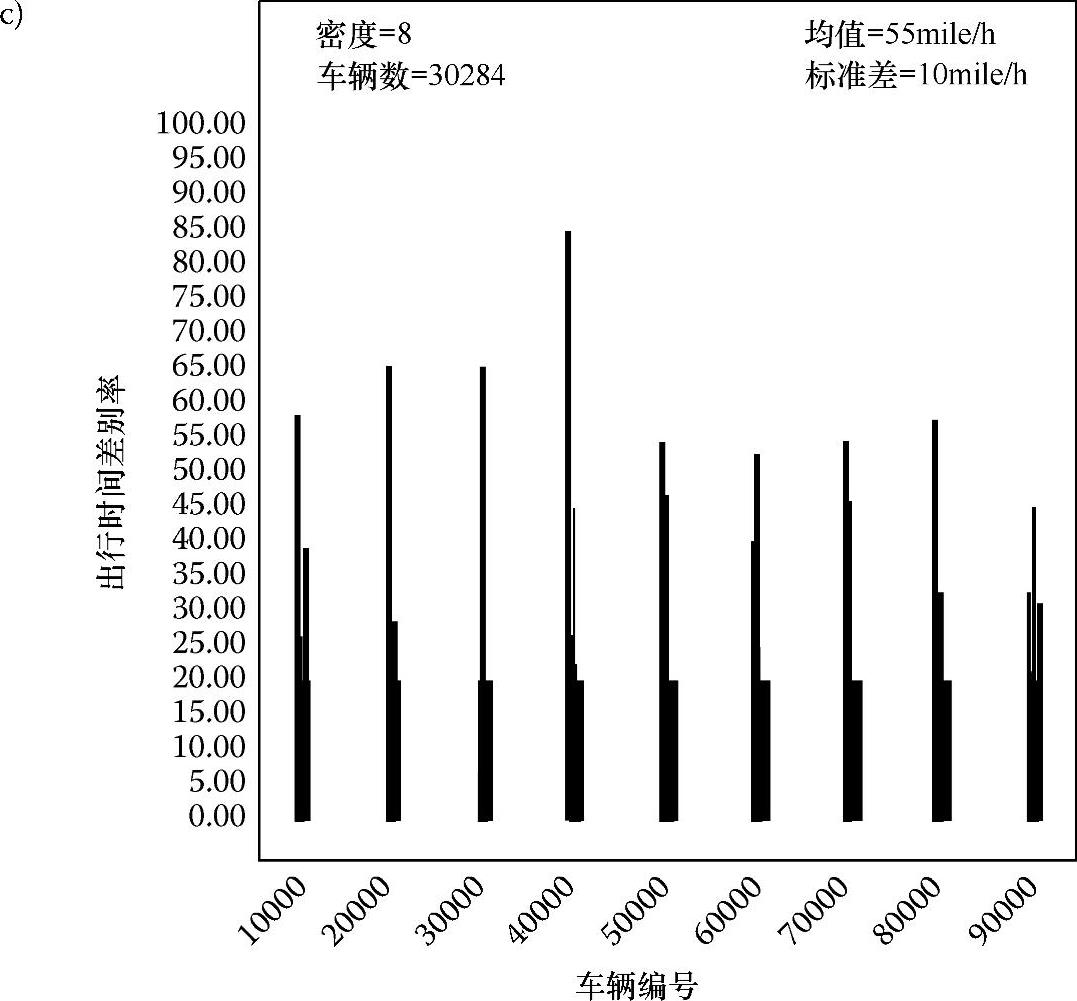
图6.11 在密度为3、6、8的情形下，所有车辆的出行时间差别率（续）

在DICAF的仿真运行全程，即在高达960s的仿真过程中，车辆一直处于DT-MC中。仿真过程能连续执行不多于1100s，直到所有车辆到达其终点。

图6.12a～c分别显示了7号路段在交通密度为3、6、8的情形下C.M.值的变化情况。根据式（6.1）的定义，C.M.值的变化是连续且一致的。选择7号路段的原因是它位于高速公路系统的中心，许多斜对角穿行的车辆都可能经过这个路段。初始化默认的C.M.值为100mile/h，当仿真时间为1100s时，所有车辆完成行驶任务，而C.M.值再次增加到100mile/h。正如所预料的那样，平均C.M.值在低交通密度时较高，在车辆总数较大时较低。

图6.13a～c显示了整个仿真过程中所有路段在三种交通密度下的C.M.平均值。可以看出，路段的平均C.M.值都非常相近，范围从54mile/h到57mile/h，这意味着DICAF中所有资源都被公平地使用了。

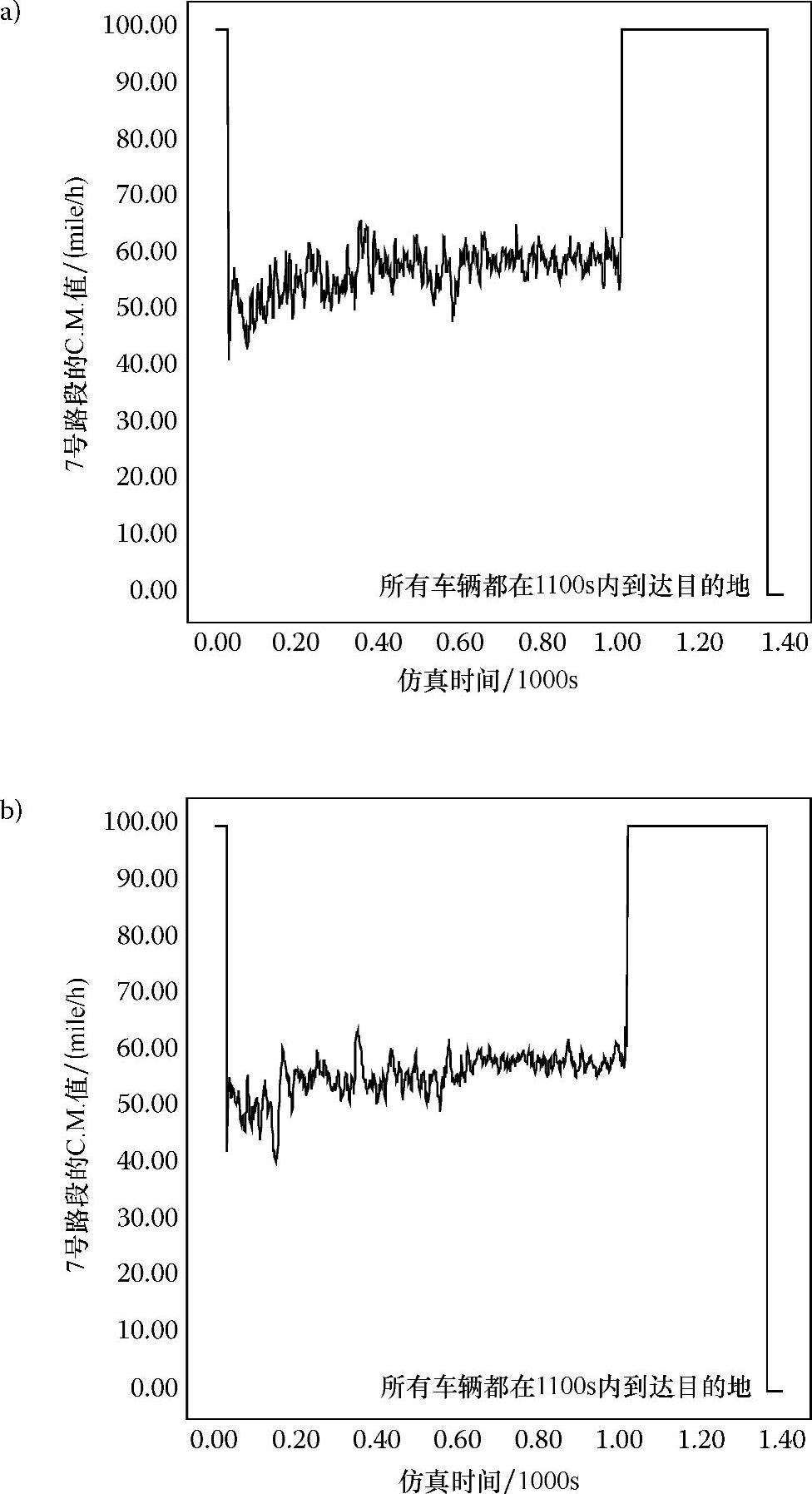
图6.12 在交通密度分别为3、6、8的情形下（分别对应图a、图b、图c）7号路段的C.M.值与仿真时间的函数关系

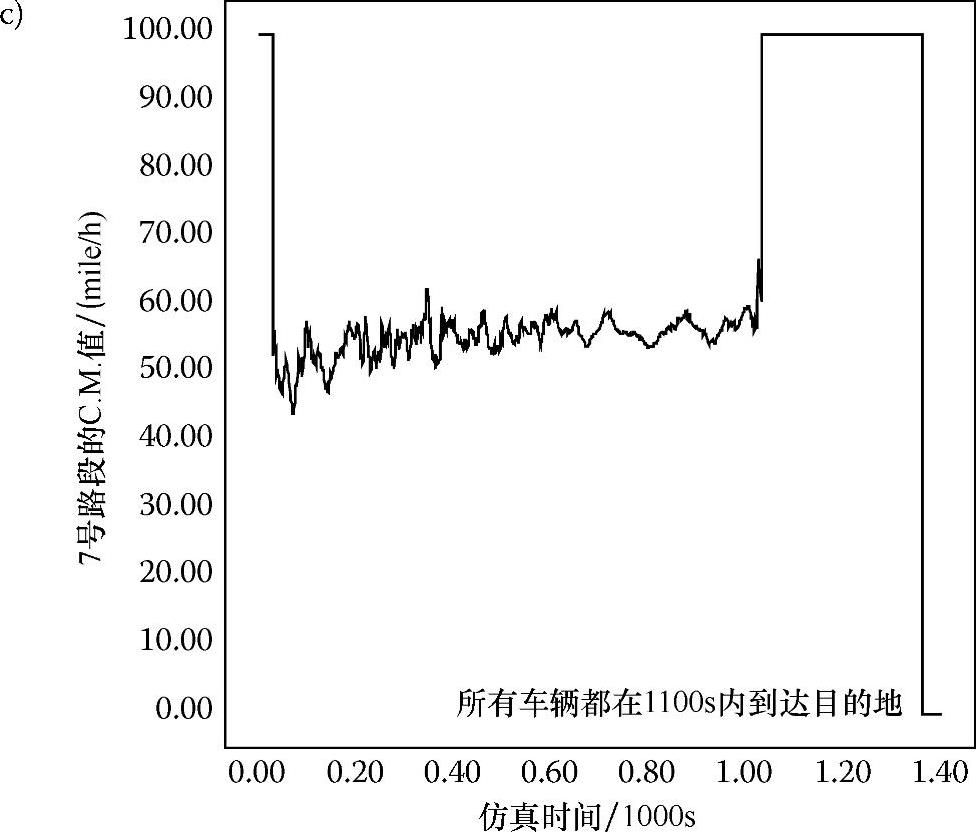
图6.12 在交通密度分别为3、6、8的情形下（分别对应图a、图b、图c）7号路段的C.M.值与仿真时间的函数关系（续）

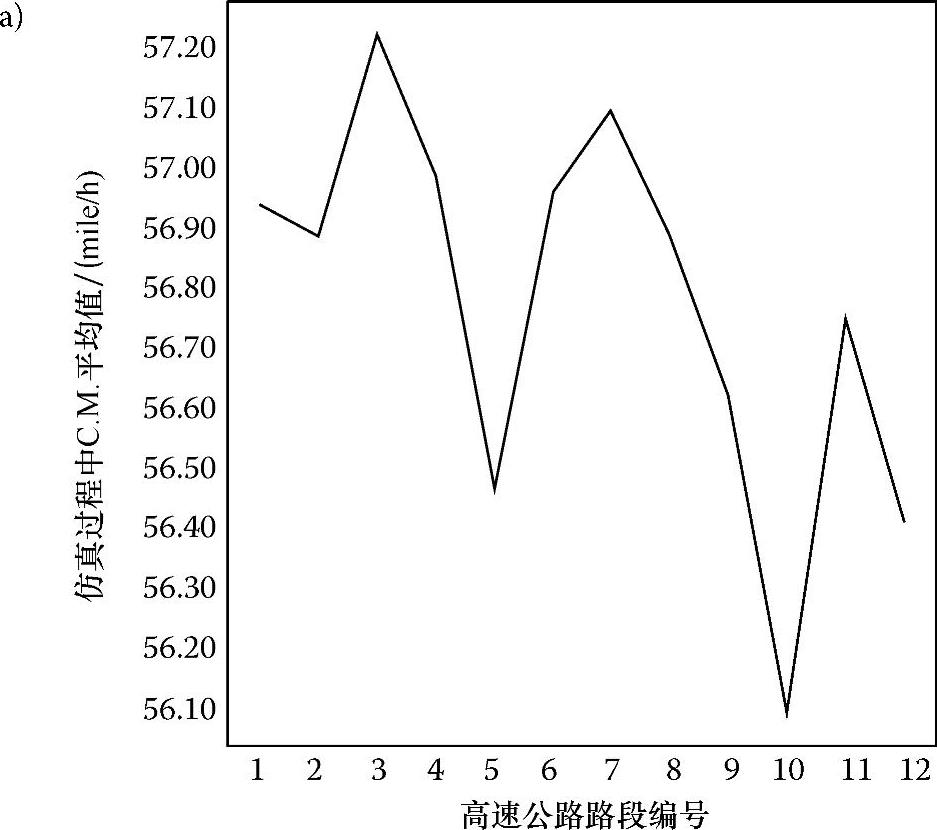
图6.13 在交通密度分别为3、6、8（分别对应图a、图b、图c）时DICAF中所有路段上的C.M.平均值

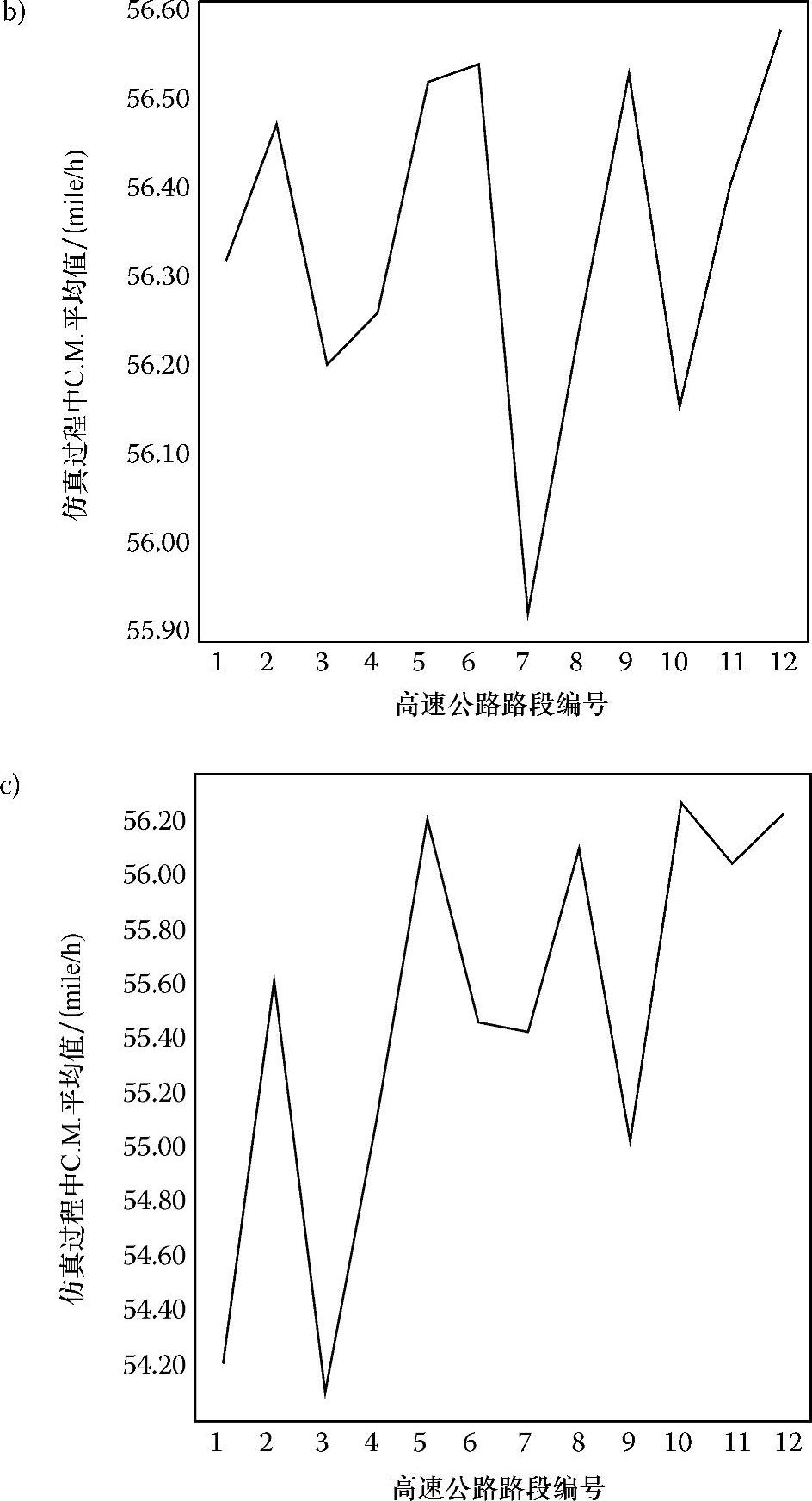
图6.13 在交通密度分别为3、6、8（分别对应图a、图b、图c）时DICAF中所有路段上的C.M.平均值（续）

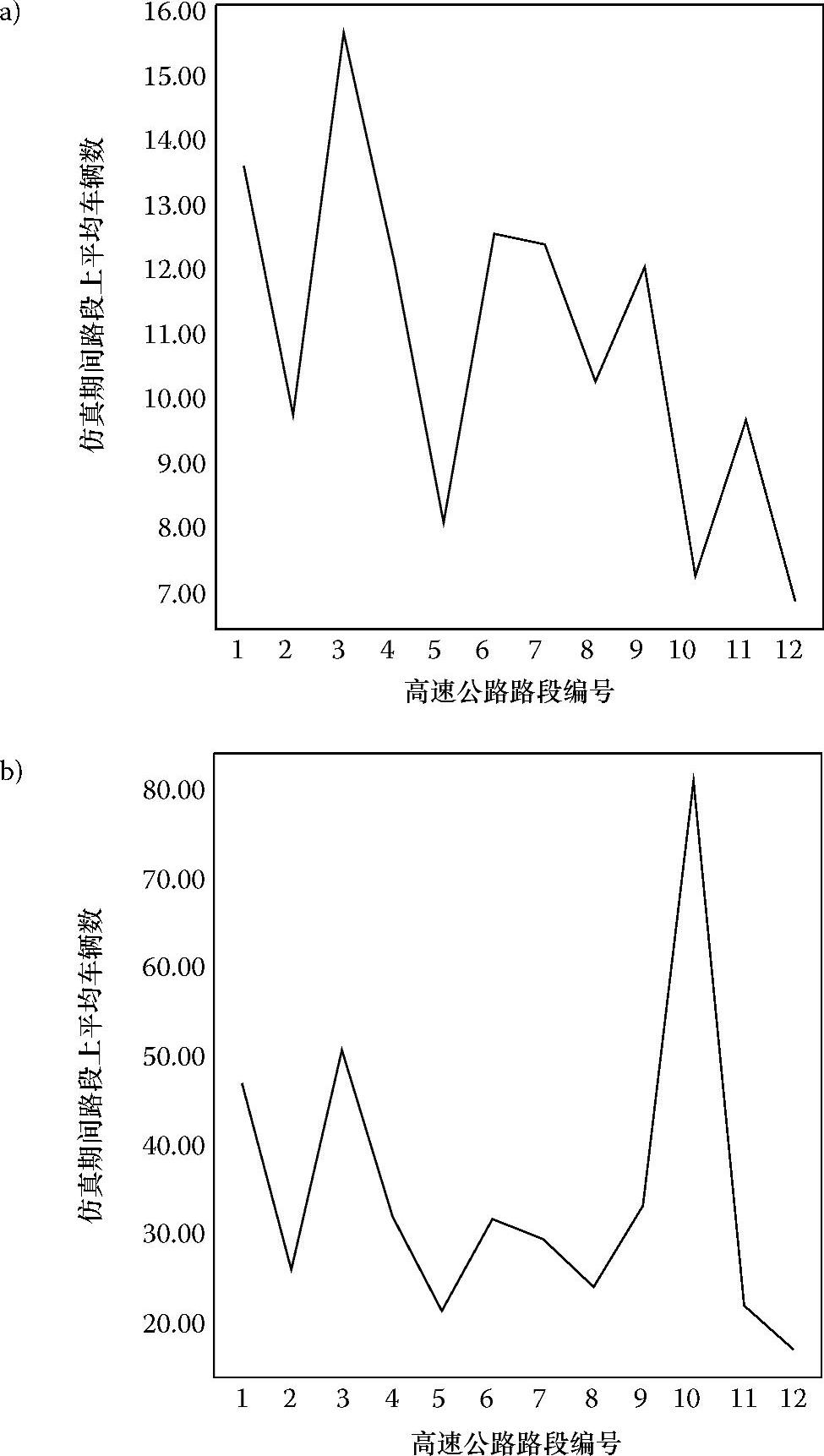
图6.14a～c通过平均车辆数曲线显示了仿真全过程中各个高速公路路段在三种交通密度下资源的利用情况。尽管所有路段都被合理利用了，反映出DICAF在成功利用所有路段资源上的优势，但是还是有某些路段上的车辆平均数远高于其他路段的情况，这主要是由于车辆的速度和终点的随机性而造成的。图6.14c中每个路段的车辆平均数高于图6.14b，而图6.14b中的数量又高于图6.14a，这是因为较高的交通密度意味着更多的车辆需要利用路段资源完成它们的行驶任务。交通密度为3时，所有路段上的最大车辆平均数为16；而交通密度为6和8时，对应的数字分别为83和130。任一路段上的车辆平均数都可以通过对每个仿真秒中该路段上的车辆排队长度进行抽样得到。要将这些数据和路段最大通行能力联系起来，可以考虑下面这种情形：假设一个高速路段最多允许2000辆车，以0～90mile/h范围内某个速度等速行驶。假设平均行驶速度为90mile/h，最短行驶时间等于10mile/h÷90mile/h=399.9s，相当于仿真时间为4.4s。于是，对每一个仿真秒而言，每条路段上最大车辆数为：2000辆÷4.4s=454辆/s。从图中可以看出DICAF中任意路段上的最大车辆平均数为130，只相当于绝对最大值的28%。因此，可以说，对于给定数量的车辆，DICAF能将交通流量在所有路段上公平地分配，而不会像传统方式那样造成一部分路段极度拥挤的状况。

(www.xing528.com)

图6.14 仿真全过程中交通密度分别为3、6、8（分别对应图a、图b、图c）时高速公路路段上的平均车辆数

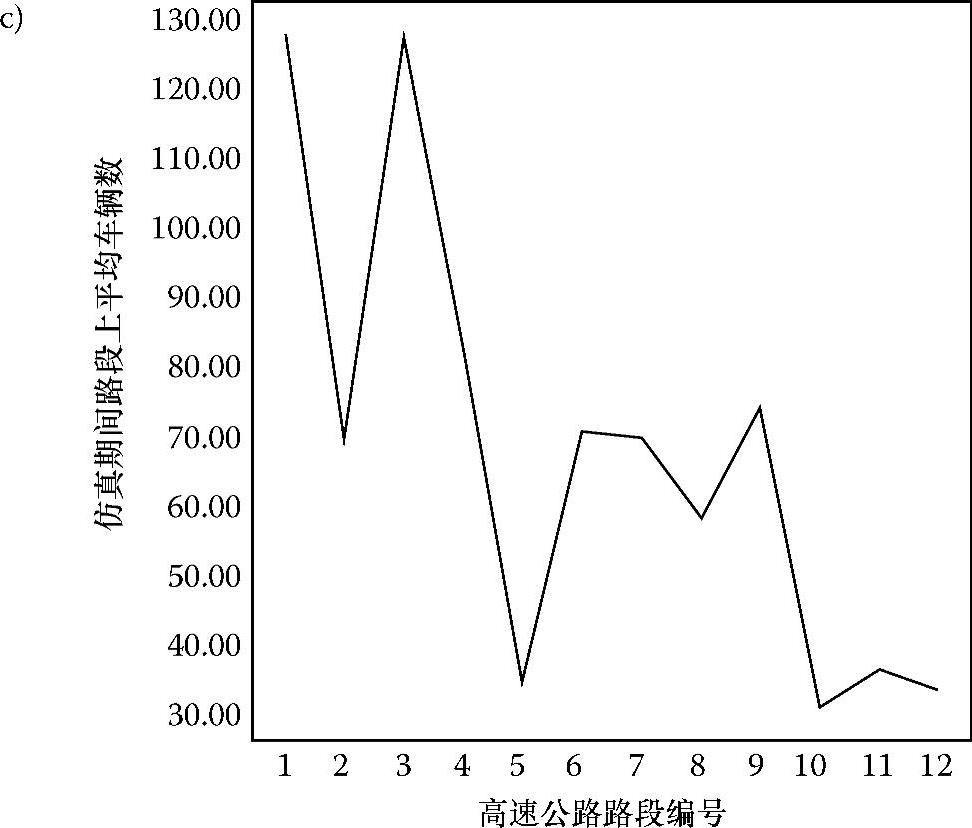
图6.14 仿真全过程中交通密度分别为3、6、8（分别对应图a、图b、图c）时高速公路路段上的平均车辆数（续）

为了理解车辆进入时间对出行时间的影响，图6.15a～c显示了所有车辆的数组关系[（一辆车的实际行驶时间与理想行驶时间之差与理想出行时间之比），车辆进入DICAF中的时间]。图6.15a～c分别对应交通密度为3、6、8的情况。图6.15a～c中黑点的增多反映出车辆的增多。除了图6.15c中600～960s间的黑色区域以外，三幅曲线图的轮廓非常相似。这意味着除了在仿真开始阶段以外，无论车辆在仿真的什么时间进入DICAF，车辆的行驶时间都保持不变。图6.15c中600～960s间的黑色区域并不明显，它只是反映了一组可预计数量的车辆在仿真时间段{600s，900s}中进入到DICAF中，对于这些车辆而言，出行时间差别率为0%～10%。然而，三幅曲线图中的负斜率都非常明显，它或者说明了图中右上角数据缺失的原因。这意味着尽管交通密度很高，DICAF仍能成功地为所有车辆选择较好的路径。可以观察到每次仿真中所有车辆都能正确到达它们的目的地，图6.15a～c中的曲线同样也表明在交通密度为3～8的条件下，高速公路系统都是稳定的，也就是说它至少可以容纳30284辆车。

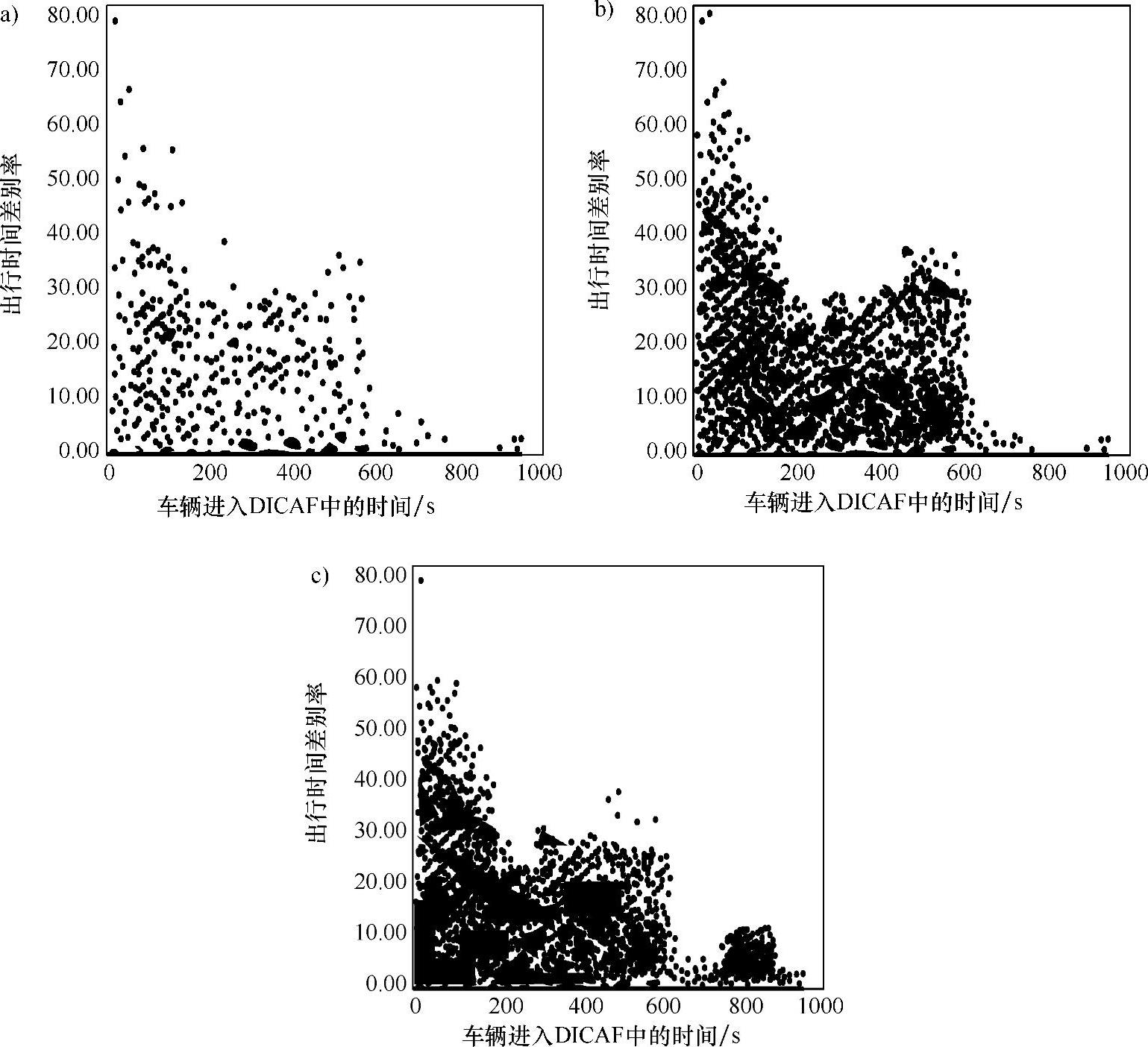
图6.15 每辆车的出行时间差别率[（车辆实际行驶时间与理想行驶时间之差/理想出行时间）×100%]，与车辆进入DICAF时间的函数关系

a）交通密度为3 b）交通密度为6 c）交通密度为8

在曲线图中，白天较早的时候进入DICAF的车辆似乎要比仿真过程中其他时间进入的车辆花费更多的行驶时间。这似乎与常理相违背，因为一般情况下早上车辆都比较少。我们可以通过检测进入DICAF的车辆的速度分布得到原因，该速度分布是仿真时间的函数，如图6.16所示。

图6.16显示了进入DICAF中车辆的速度情况，范围从30mile/h到90mile/h，仿真时间从0s到100s。从100s到550s，速度带宽会缩小为40mile/h到80mile/h，接下来，速度带宽会不断缩窄，直到第960s时，速度范围缩窄为50～70mile/h。如果要使车辆速度服从正态分布（见图6.10），交通发生器程序必须首先建立对应于不同速度带宽{30mile/h，35mile/h}到{85mile/h，90mile/h}的“速度组”，然后分别针对三种交通密度情况给每组分配适当的车辆数。接下来，产生速度和目的地都是随机值的车辆，它们在仿真时间为0s时被分配至合适的组中。正如预期的那样，这些包括极限值{30mile/h，35mile/h}和{85mile/h，90mile/h}速度带宽的组首先被填满。然后，在仿真时间的100～550s，速度带宽为{40mile/h，45mile/h}、{45mile/h，50mile/h}、{70mile/h，75mile/h}、{75mile/h，80mile/h}的组也相继被填满。到此时为止，除了{50mile/h，70mile/h}这个速度区间外的所有组都被填满了。所以，在550～960s间，DICAF中的车辆的速度分布在很窄的范围内。

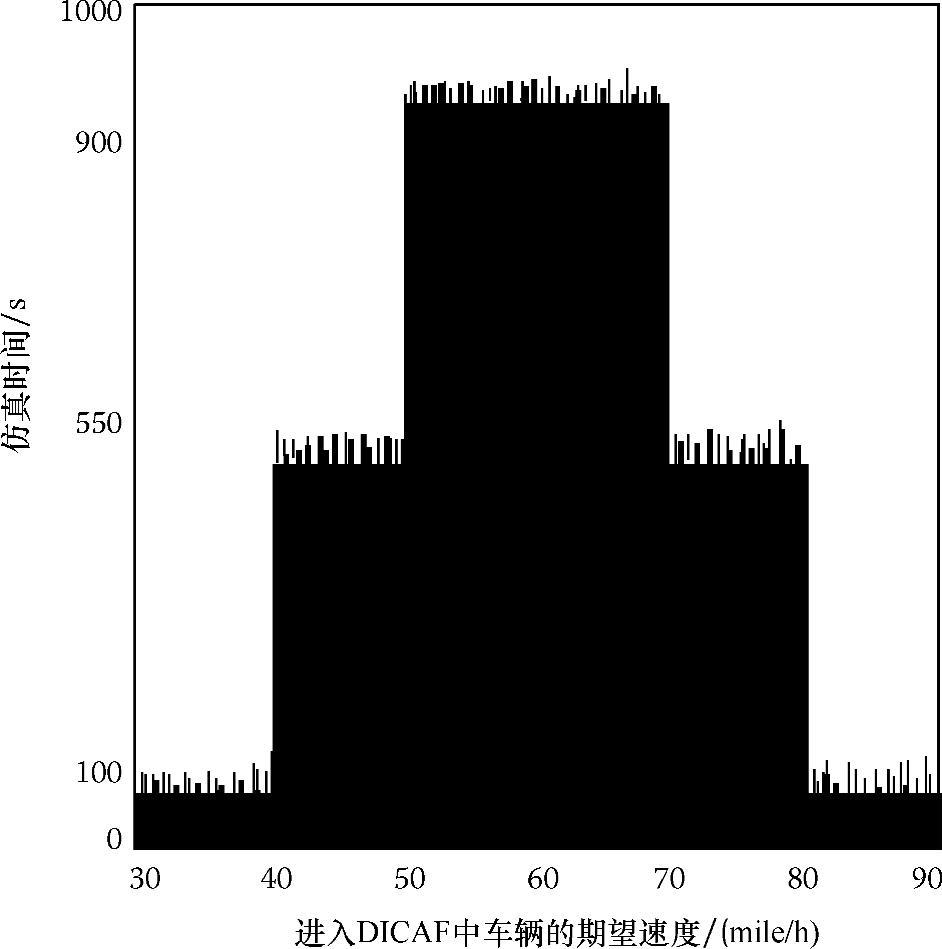
图6.16 交通密度为8时进入DICAF中车辆的期望速度和仿真时间的函数关系

从逻辑上来讲，车辆速度的下降很可能会导致路段C.M.值的下降。因此，除了那些低速车辆会花费较长的行驶时间以外，那些有着较高期望速度的车辆也会需要更长的行驶时间。随着仿真的进行，可以看到车辆的平均期望速度逐渐增加，从而产生更快的出行和更短的出行时间。

此外，比较图6.17和图6.10中的曲线，可以看出实际车辆速度分布与初始的期望正态分布有些相似，但是图6.17中的分布因为拥堵的存在而显得有些扁平。

图6.17显示了每辆车的实际平均速度，是用每辆车的总出行距离除以它们各自的出行时间来得到的。可以观察到，在整个仿真过程中，大多数车辆都以30～80mile/h的平均速度行驶，而超过75mile/h的车辆数非常少。平均速度集中在60mile/h左右，这意味着尽管有30000多辆车在争夺道路资源，在DICAF中大多数车辆还是能够有效地进行路径决策，并实现在较短出行时间内完成出行任务的目的。

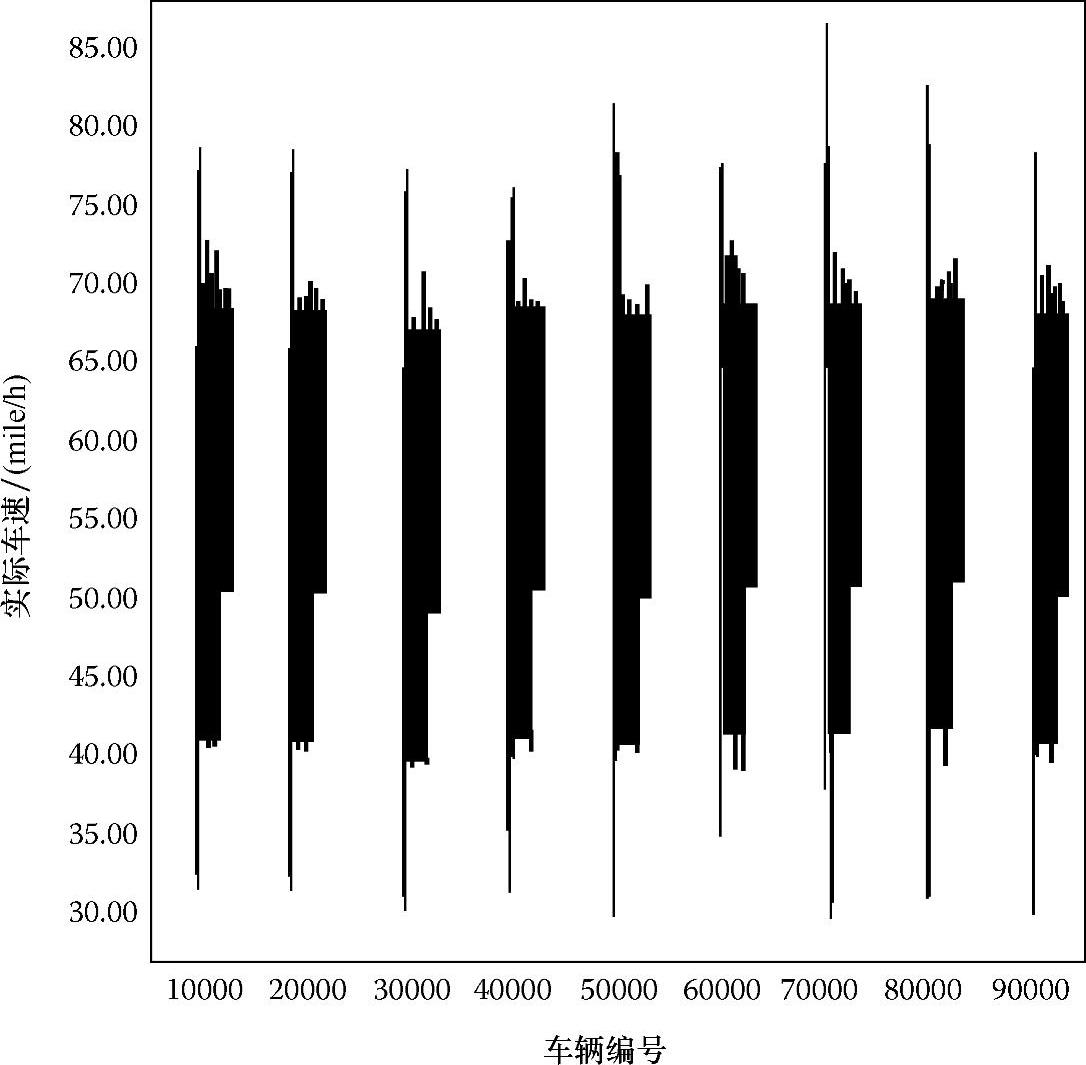
图6.17 交通密度为8时DICAF中车辆的实际平均速度

在仿真刚开始阶段就进入DICAF中的车辆，与后来进入的车辆在出行时间差别率上的对比如图6.15所示，图中可以看出较窄的速度带宽对所有车辆有效选择路径和实现更快出行有着重要的作用。为了检验这个假设，我们设计了在以下两种交通输入参数情况下进行的仿真：{μ=65mile/h，σ=10mile/h}和{μ=65mile/h，σ=5mile/h}，交通密度选择为8。图6.18a和图6.18b显示了所有车辆的实际出行时间与理想出行时间之差，与理想出行时间的比值。图6.18a对应的交通发生器参数为{μ=65mile/h，σ=10mile/h}，图6.18b对应的交通发生器参数为{μ=65mile/h，σ=5mile/h}。在图6.18a中，车辆总数为30284，平均差和标准差分别为1.11%和4.13%。在图6.18b中，车辆总数为30302，平均差和标准差分别为0.03%和0.45%。

与图6.11c中相关数据的比较显示出，要提高出行效率，即使所有车辆的总出行时间更短，可以通过定义最大速度和最小速度，将速度限制在较狭窄的范围内而得到，而不是像当前政策那样仅以最大速度55mile/h作为限制。可以想象，在现有的高速公路系统中，车辆速度波动的主要原因是缺乏高速路段的信息，比如出口的位置和速度等，这些信息都是可以从DICAF中获得的。

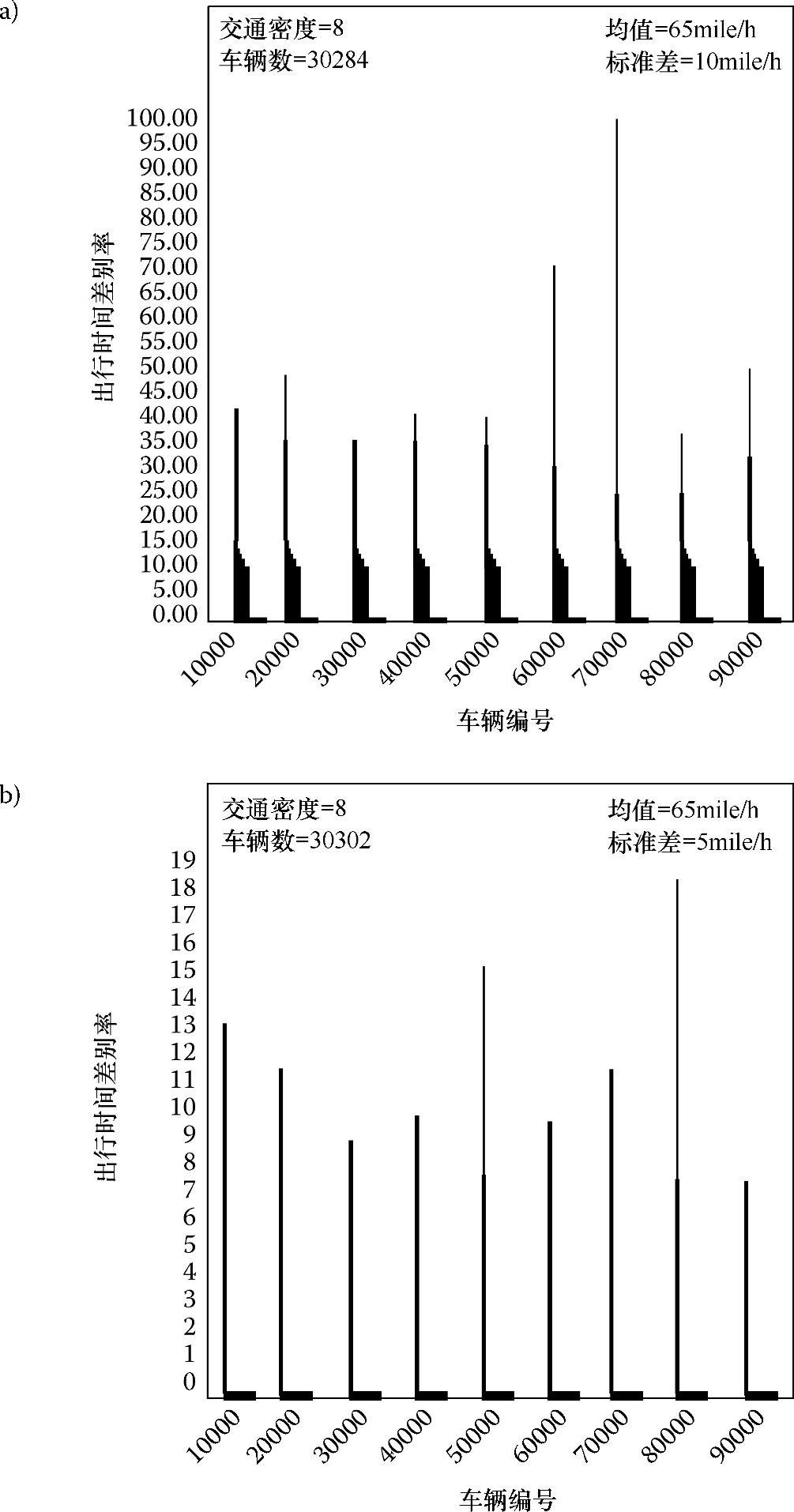
图6.18 交通发生器参数为{μ=65mile/h，σ=10mile/h}（图a）、{μ=65mile/h，σ=5mile/h}（图b）情况下所有车辆的出行时间差别率（续）

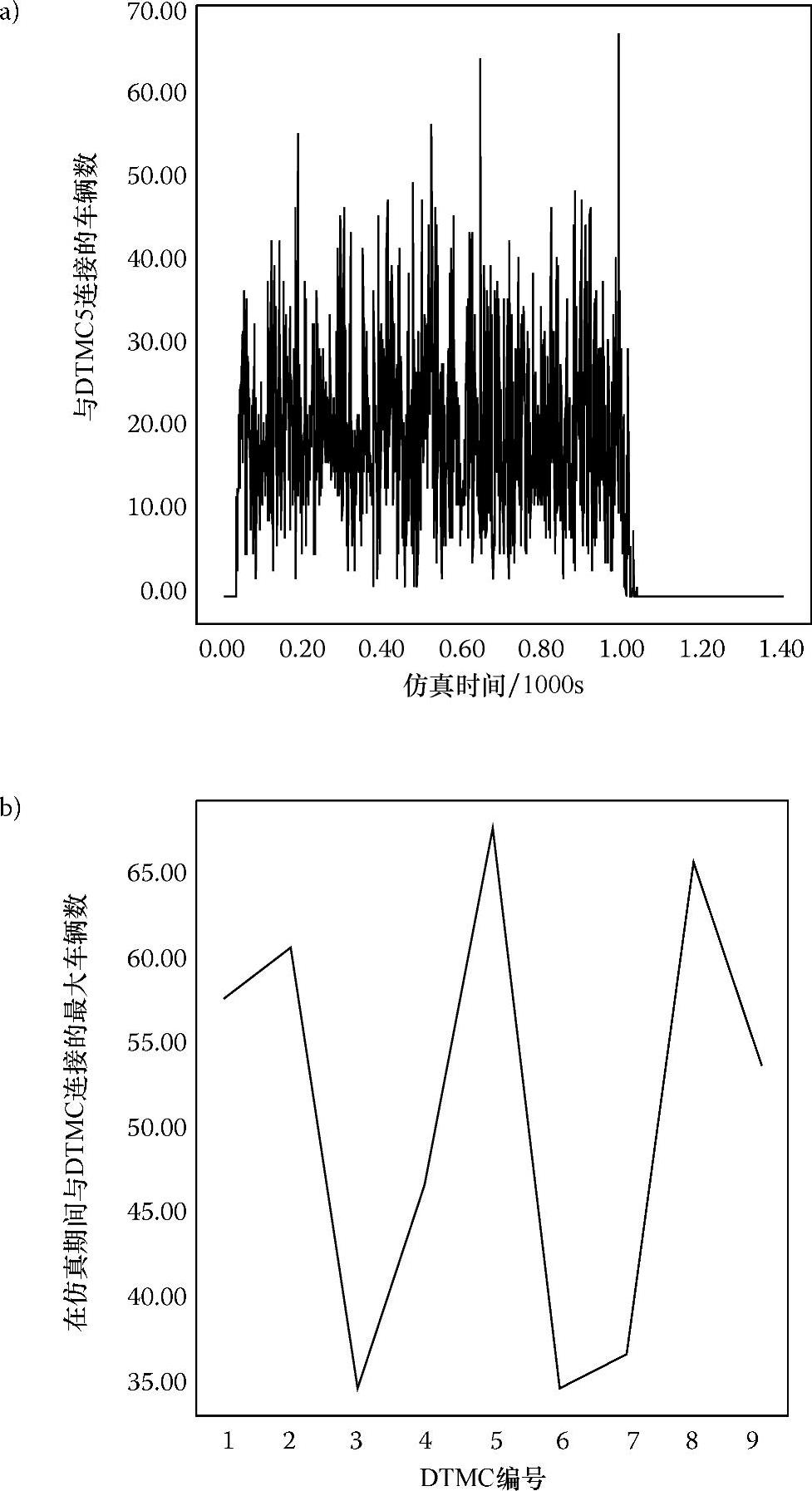
图6.19 与DTMC5连接的车辆数和仿真时间的函数关系（图a）以及与DTMC连接的最大车辆数的分布（图b）

DICAF的一个基本目标就是公平地将所有通信任务分配给所有实体。图6.19a展示了与DTMC5连接的车辆数的分布情况，它是仿真时间的函数。正如之前所分析的那样，选择DTMC5的原因是它位于高速公路系统的中心，很有可能位于许多车辆的必经之路上，所以，研究这个DTMC中与数据有关的通信问题可以反映可能遇到的最坏的情况。图6.19a还反映出任意路段上的车辆数，以及路段的C.M.值都是和时间高度动态相关。图6.19b显示了与DTMC连接的最大车辆数的分布情况。图6.19a和图6.19b所展示的数据是通过对每个仿真秒中的排队长度进行抽样而获得的。当车辆与DTMC连接时，车辆会下载相应路段的C.M.值，平均信息长度为96B。由于DTMC5中最大车辆数为68，因此DTMC5与车辆间的最大通信速率等于68×96B/仿真秒=6528/1.5B/min=4.352B/min。这种通信速率很容易通过9600bit/s或19200bit/s的商业无线调制解调器来实现。

图6.20a显示了DTMC5处发送和接收的泛洪消息的数量分布，它是仿真时间的函数。选择DTMC5的原因在前面也提到过。对于每个DTMC来说，DTMC内部接收和发送的最大泛洪消息数量会被记录下来，并制成曲线图，如图6.20b所示。可以观察到在每个DTMC中，最大泛洪消息数是与仿真开始同时发生的，原因如下：一旦车辆进入高速路段，所有DTMC都会计算其所控制的路段上的新的C.M.值。新的C.M.值很有可能与预先默认的100mile/h不同，因此会被立即传播给其他DTMC。随着仿真的进行，C.M.值逐渐增加，而消息泛洪的频率逐渐下降。图6.20b的曲线是针对交通密度为8，即有30284辆车在路段上行驶的情况，通过对仿真中每秒内的消息队列进行抽样得到的。每条泛洪消息包含4个字段，需要16B。图6.20b中，泛洪消息的最小和最大数量分别为55和122，相应的数据通信速度为55×16B/仿真秒=55×16/1.5B/min=586B/min，122×16B/仿真秒=122×16/1.5B/min=1301B/min，同样很容易通过9600bit/s或19200bit/s的商业无线调制解调器来实现。假设仿真过程需要1s或者实际的1.5min，那么这里显示的数据也是在1.5min内的。

因此，图6.19和图6.20可以证明，DICAF的一个主要目标，即建立一个不太昂贵的、成本效益比较高的高速公路体系，该目标已经实现了。相比之下，集中式算法在理论上需要更高的通信速率，这意味着需要价格更加昂贵的接口。

图6.21a和图6.21b显示了图6.9所示的大型复杂的高速公路系统的模拟和仿真结果。这项研究的目的就是要检测DICAF中异步分布式算法在一个拥有50个DTMC和45296辆自治车辆，同时在51个工作站上执行的大规模系统中的实用性。图6.21a和图6.21b中的曲线对应于交通密度为3时，实际高速公路24h的运营情况，交通发生器参数为μ=65mile/h，σ=5mile/h。图6.21a显示出均值和标准差分别为0.038%和0.577%，这表明尽管有45296辆车在竞争路段资源，车辆平均行驶时间仅超过绝对最小值0.038%。图6.21b表明，除了那些在仿真开始阶段就进入DICAF的车辆外，其他时刻进入DICAF的车辆都能成功到达终点，且平均行驶时间与进入DICAF的时刻无关。我们还有其他一些观察有9个DTMC的系统得到的曲线图，也显示了同样的行为特征，这里就不再赘述。

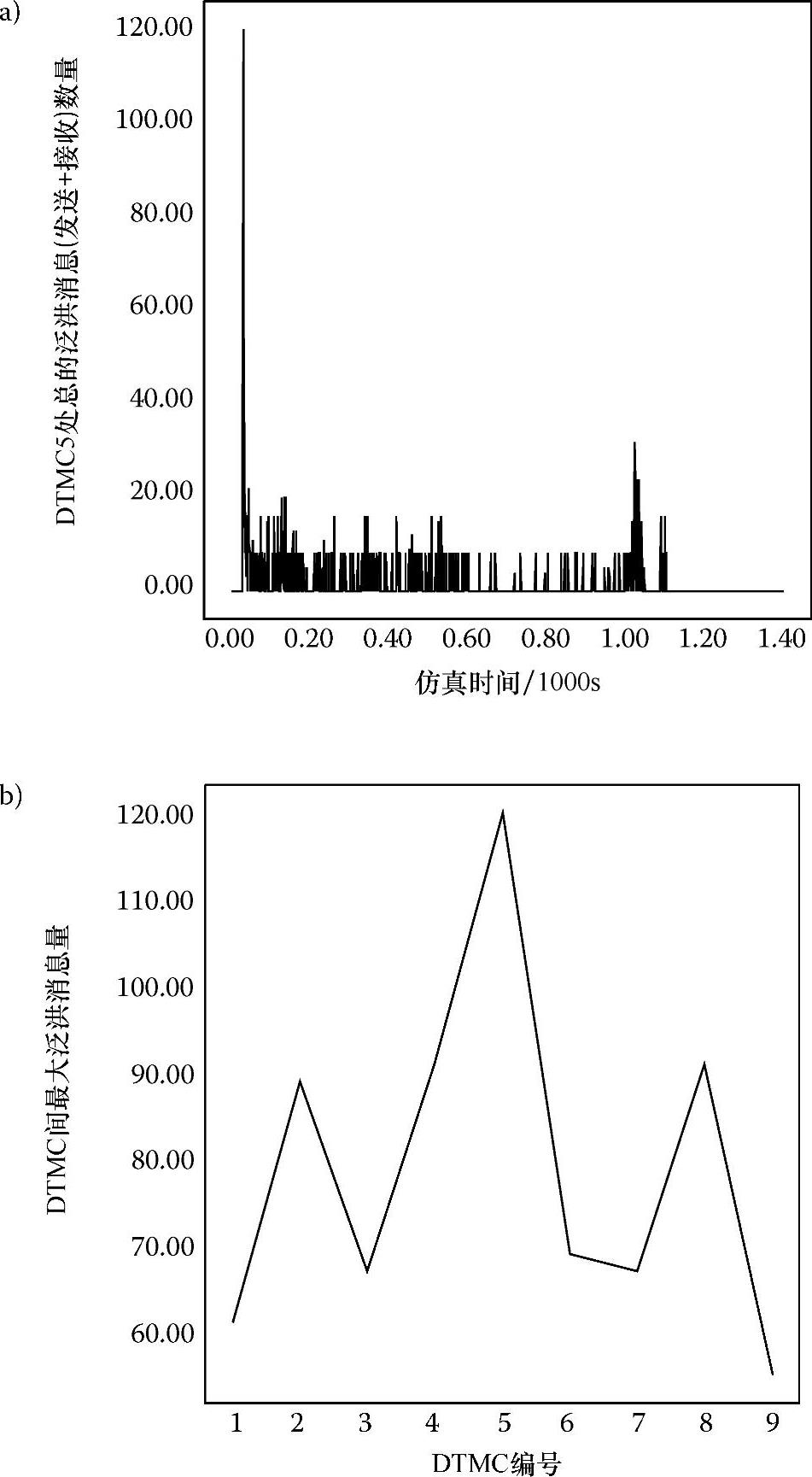
图6.20 DTMC5处的DTMC间泛洪消息数量和仿真时间的函数关系（图a）以及每个DTMC中处理的DTMC间最大泛洪消息量（发送+接收）（图b）

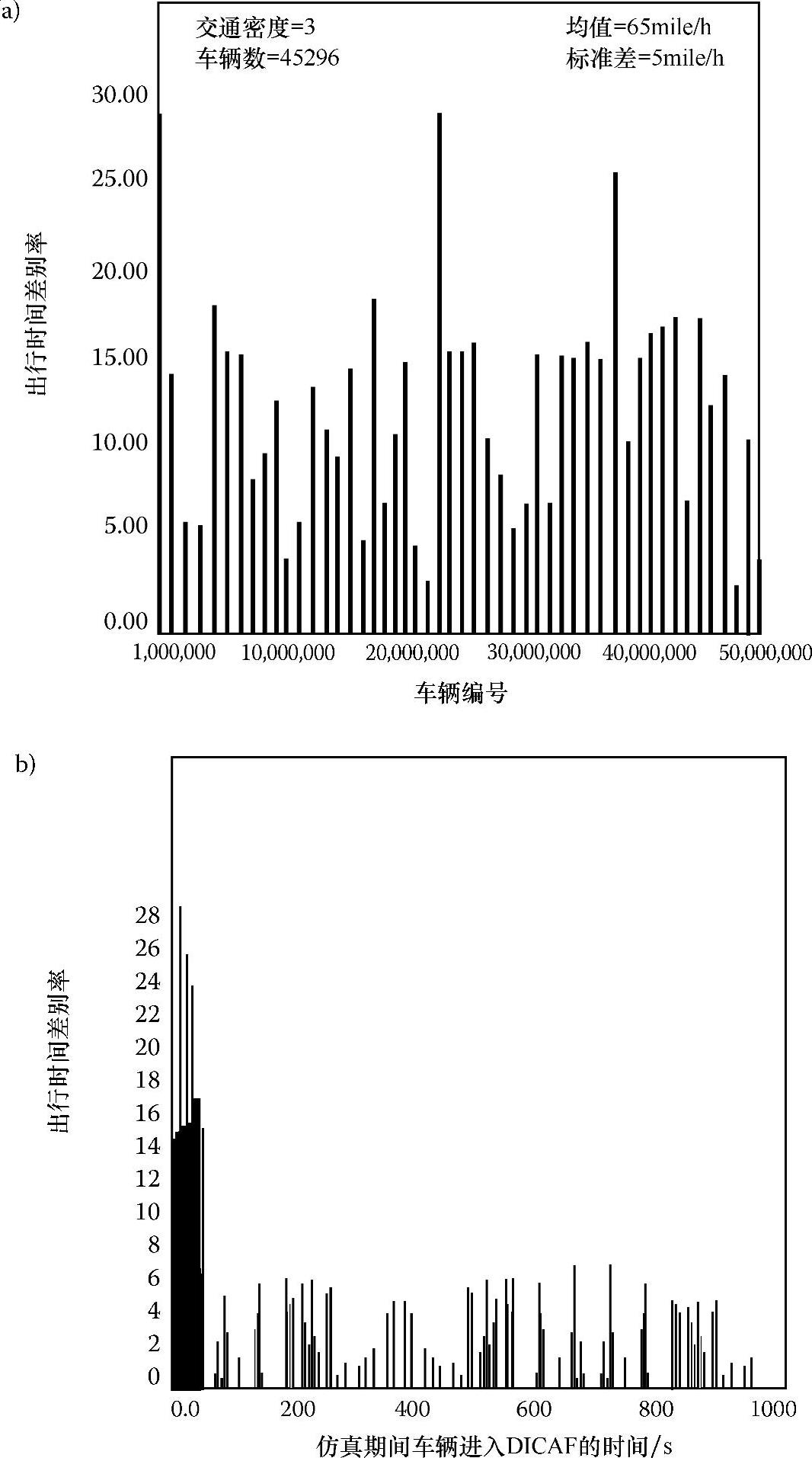
图6.21 在DICAF中有50个DTMC的公路系统的仿真结果：出行时间差别率

a）对所有车辆 b）与车辆进入DICAF时间的函数关系

DICAF的缺陷

本章中没有考虑交通事故、突发事件和可能由此产生的拥堵问题。因此本章考虑的拥堵问题仅仅是由DICAF中车辆速度和终点选择的随机性造成的。一般来说，任何路段的上下行方向的C.M.值应该是不同的，而DICAF中假设上下行方向的C.M.值相同。但这种假设是合理的，因为DICAF中车辆的目的地是随机的，所以上下行车辆数量很可能基本相同，因此也就具有了相同的C.M.值。本章的目的是针对一些有代表性的高速公路系统，研究DICAF的一般性能，而不是对特定的联邦和州际公路的实际交通情况进行精确模拟。因此，我们假设交通分布与数据选取日期没有关系。正如本章前面所提到的，当用一个工作站模拟一个DTMC时，每辆车都模拟为一个进程。进程从一个DTMC传递到另一个DTMC，并由车辆所在地管辖的DTMC中的工作站执行。选择该方法的主要原因是我们无法获得包括45000个相互连接的工作站的试验台。如果模型与实际不符，是有利有弊的事情。坏的一面是不能详细模拟DTMC和车辆之间建立联系的过程。并且，DTMC和车辆之间在某特定操作系统下进行的数据交换在实际中会很慢，因为仿真过程中交换的是本地的数据结构。好的一面是本章展示的实验数据都可以保存在50个工作站中，这些工作站承担了45000多辆车中每辆车的路径计算任务。由于在实际中是由每辆车的计算引擎计算它自己的路径，所以基于DICAF开发的系统在实际中的性能表现很有可能会大大超过本章在仿真中预测的值。