DARYN智能性能：设计成果

本节将详细介绍在ARMSTRONG系统中做过的许多实验，以评估DARYN算法的性能。在实验中一共有4个铁路网络，分别包括4、6、9和12个站点，这些站点都被模拟为ARMSTRONG的节点。要模拟更大些的网络是很困难的，因为ARMSTRONG的硬件限制了协议的数量以及同时打开所有节点相关文件的指针数量。这4个网络如图4.10所示。本节还将介绍DARYN的局限性。

为了评估DARYN的性能，我们提出了三项措施。首先，将模拟过程所需的CPU时间与传统的集中式方法需要的CPU时间相比较，根据不同的网络规模、列车数量和列车速度来计算加速因子。加速因子是指完成分布式仿真所需的CPU时间与单处理器仿真所需的CPU时间之比。由于DARYN是异步的，对终端的检测过程会非常复杂，所以我们可以这样近似地认为：系统中可能会有些行驶路线特别长的列车，它的速度是专门设定的，以确保其他所有列车都能比它先到达目的地，我们以下称其为专列。所以，完成整个过程所需的全部CPU时间是由这种长线路专列在线路上运行所花费的时间决定的。某专列从一个处理器开出，到达目的地，也就是ARMSTRONG中另一个节点。我们可以将火车开出时起始节点的计时器的值作为火车的起动时间参数start_time。虽然节点是异步的，但是它们的计时器都在初始化时复位到零，并且假设它们的频率差异非常小。start_time和专列到达目的节点的时间之差，就是所需的CPU时间。

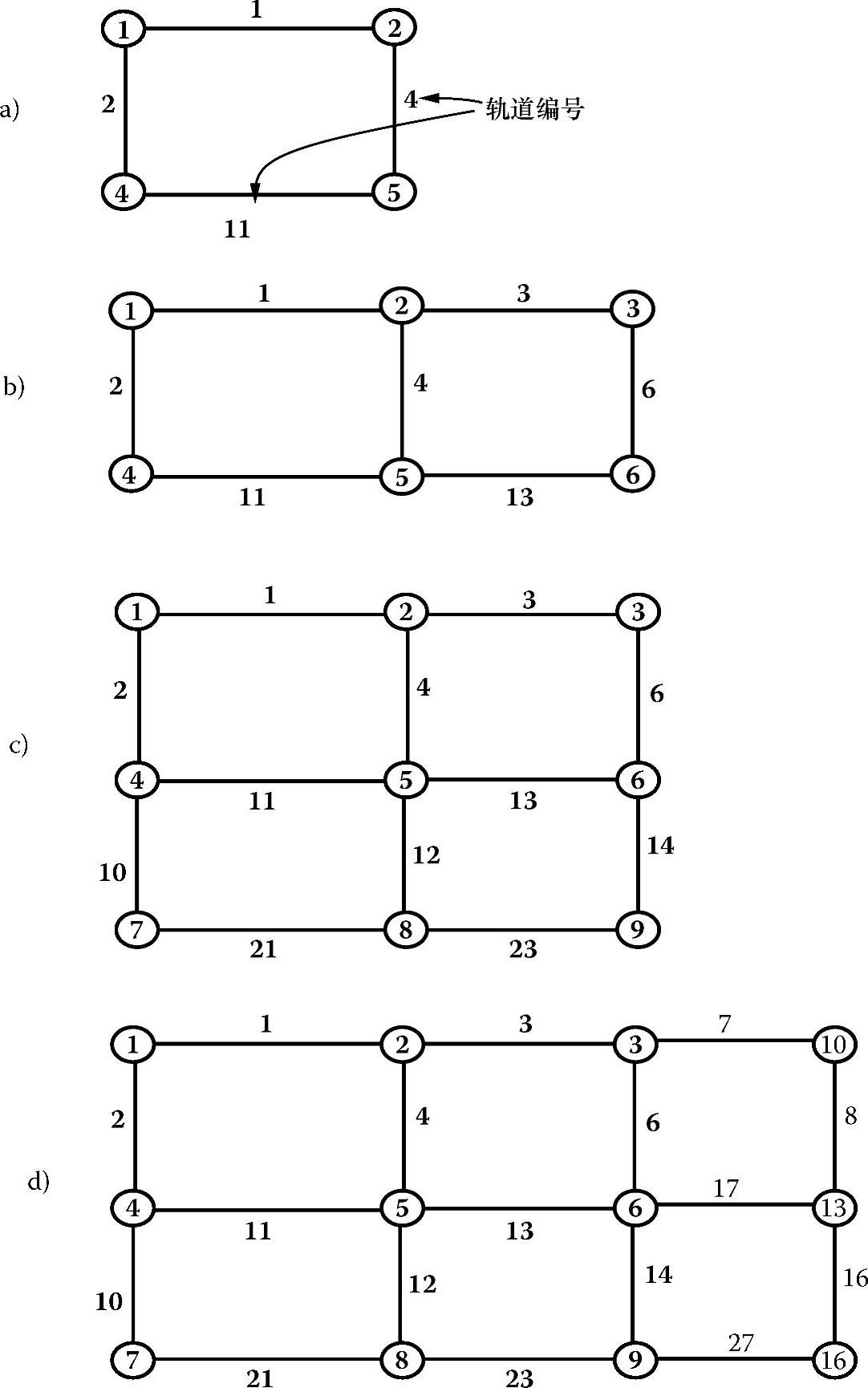
图4.10 用于评估DARYN算法性能的4个轨道网络

第二项措施，是基于这样一个依据：如果DARYN算法具有可扩展，那么一列火车以固定的速度运行固定的距离所需的CPU时间，就不会明显地受到整个系统内火车数量和网络规模的影响，因为网络规模和火车数量的任何增长，一定会伴有相应比例的计算引擎数量上的增加。CPU的运行时间可能对系统中运行的火车数量有些影响，但不会影响车站的数量，因为数量增加后的车载计算机还是可以和原定数量的车站计算机实现交互。分布式仿真的这项措施主要是为了和相应的集中处理器的执行情况相对比。

第三项措施是测量“闲置时间”。一列火车在所经过的所有节点上都要与车站计算机互动以获得轨道使用权，那么它在所有节点上停车且等待分配的累计时间就是“闲置时间”。闲置时间也包括它计算未能执行成功的最佳路径所需的时间。这项措施也是针对相应的集中处理器的执行情况实施的。

传统方法中造成集中调度通信延迟的一个很明显的原因是因为需要定期读取每列火车的位置和速度，以及每条轨道的状态。这在单处理器上模拟时会产生约0.7ms的延迟。

回顾一下，为了解决分布式仿真的时间问题，我们曾经把实际行驶时间当做延迟来模拟。在分布式和集中处理器仿真中，这些延迟都以同样的方式减缓了仿真速度，这就意味着我们能够得到一致的CPU运行时间，即决策时间与行驶时间之和，而不仅仅只能得到决策时间。因为这项研究的主要目的是对DARYN中分布式决策的性能进行评估，所以接下来我们要做这样一些事情：这两种仿真的CPU运行时间都可以通过按比例改变行驶延误，并通过绘图得到。两种情况下观察到的图形都是线性的，这意味着，行驶延误按比例线性地减缓了两种仿真的速度。在行驶延误等于0时，CPU运行时间可以由这些图直接推算得出。在单处理器的情况下，可以看到推算出的数据与另一个不模拟行驶时间延误时的仿真结果完全一致。

此外，据观察，集中处理程序在Sparc1+工作站上执行的速度比ARMSTRONG^[32]系统中每个处理器的速度都快大约8.56倍。因此，必须将所有集中处理器的原始数据都按比例扩展8.56倍，然后才能与分布式仿真数据进行比较。

首先，考虑一个由4个节点和4条轨道组成的铁路网。其中，变量为列车的数量，取值范围从2～11时，分别记录相应的CPU运行时间。第二、三和第四个网路分别包括6个站和7条轨道、9个站和10条轨道以及12个站和17条轨道。在每个网络中，变量都是列车的数量，其取值范围分别为{3，24}、{4，36}和{6，48}。此外，对于所有的实验，在火车的起点和终点的选择上都考虑了地理位置分布的均匀性。火车的速度是随机分配的。我们可以观察到CPU运行时间的变化特征在所有情况下都是一致的。从图4.11a中可以看出，在全部4个网络中，推算出的分布式仿真需要的CPU运行时间都是火车数量的函数。图4.11b显示出这一特性在传统算法中也是类似的。可以看出DARYN图的斜率比传统方法小很多。图4.11b的CPU运行时间指的是Sparc 1+工作站的标量数据，即它们反映的是原始数据乘以8.56的值，以便于和图4.11a中相应的数据进行比较。

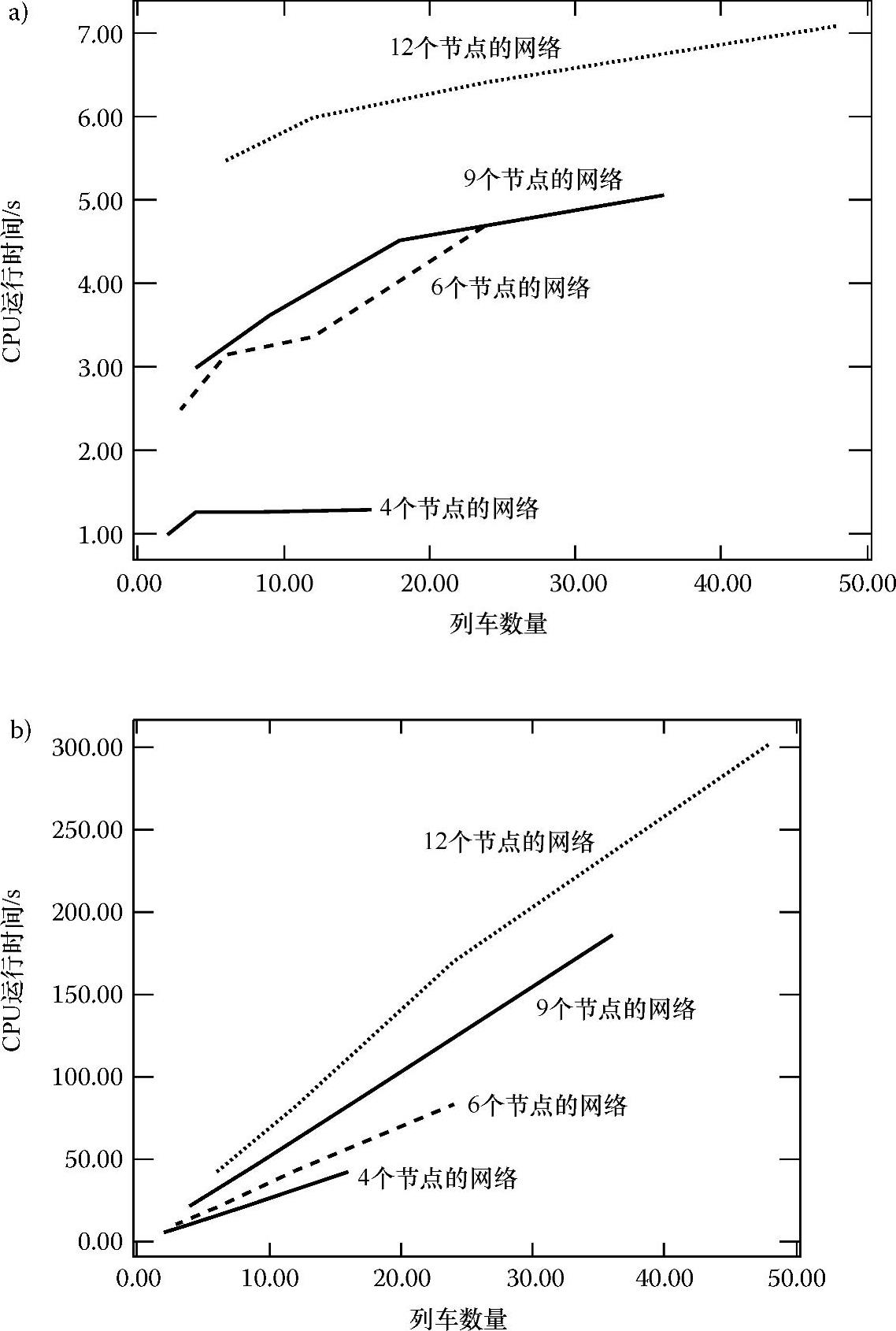
图4.11 4个网络中CPU运行时间与列车数量的函数关系图

a）DARYN算法 b）传统方法(www.xing528.com)

图4.12表示4个网络中分布式算法相对于传统算法的加速因子与火车数量之间的函数关系。加速因子等于分布式仿真与集中处理器仿真的CPU运行时间之比。当有48列火车和12个站时，加速因子是43。这个加速仅用了12个处理器来实现，并不违反任何热力学原理。它仅仅反映了这样一种情况，即随着问题规模的扩大，集中处理器会因为通信延迟的不断增大而导致运行速度越来越慢。

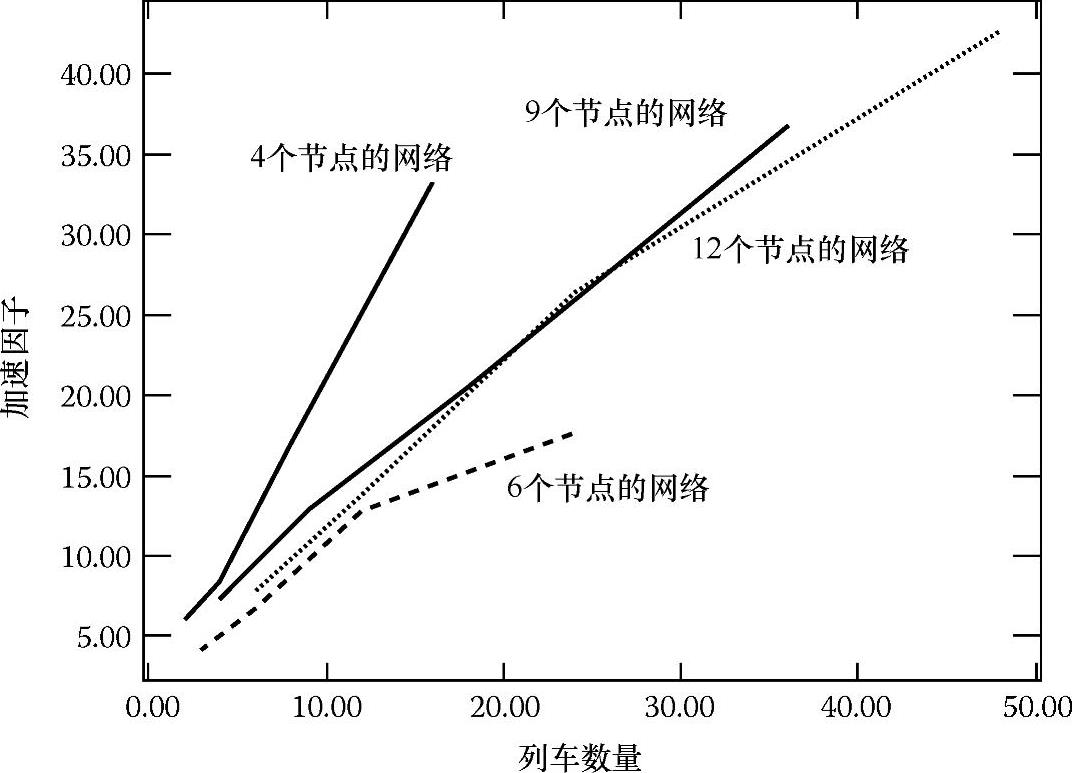
图4.12 4个网络中加速因子与列车数量的函数关系图

图4.13体现了算法性能的第二个种测量方式。一列火车以固定的速度行驶固定的距离所需要的CPU运行时间应该在不同条件下分别注明，因为火车的数量和网络规模都可能会不同。图4.13a是分布式仿真算法需要的CPU时间，而图4.13b则是集中处理器需要的CPU时间。可以看出，图4.13b的斜率很大，而图4.13a的相对小很多，这意味着分布式决策优于集中式决策。此外，随着铁路网规模的增长，正如所预期的一样，随着时间的推移，DARYN算法性能退化相对较慢，这意味着DARYN有很强的成长潜力。

最后，在4个网络中按不同的列车数量分别绘制特长专列的累计闲置时间曲线。闲置时间是指当火车停靠在某站点计算最优路径、决策，以及与车站计算机交互以获得所选择的轨道许可的过程中，闲置在该车站的时间。闲置时间也是衡量DARYN效率的一个指标，因为它反映了宝贵的列车资源的浪费情况。图4.14a表示的是DARYN算法中累计闲置时间与列车数量的关系，而图4.14b表示的是传统算法中累计闲置时间与列车数量的关系。虽然这个图不太容易看，但是很明显图4.14a中的闲置时间比图4.14b要少得多。

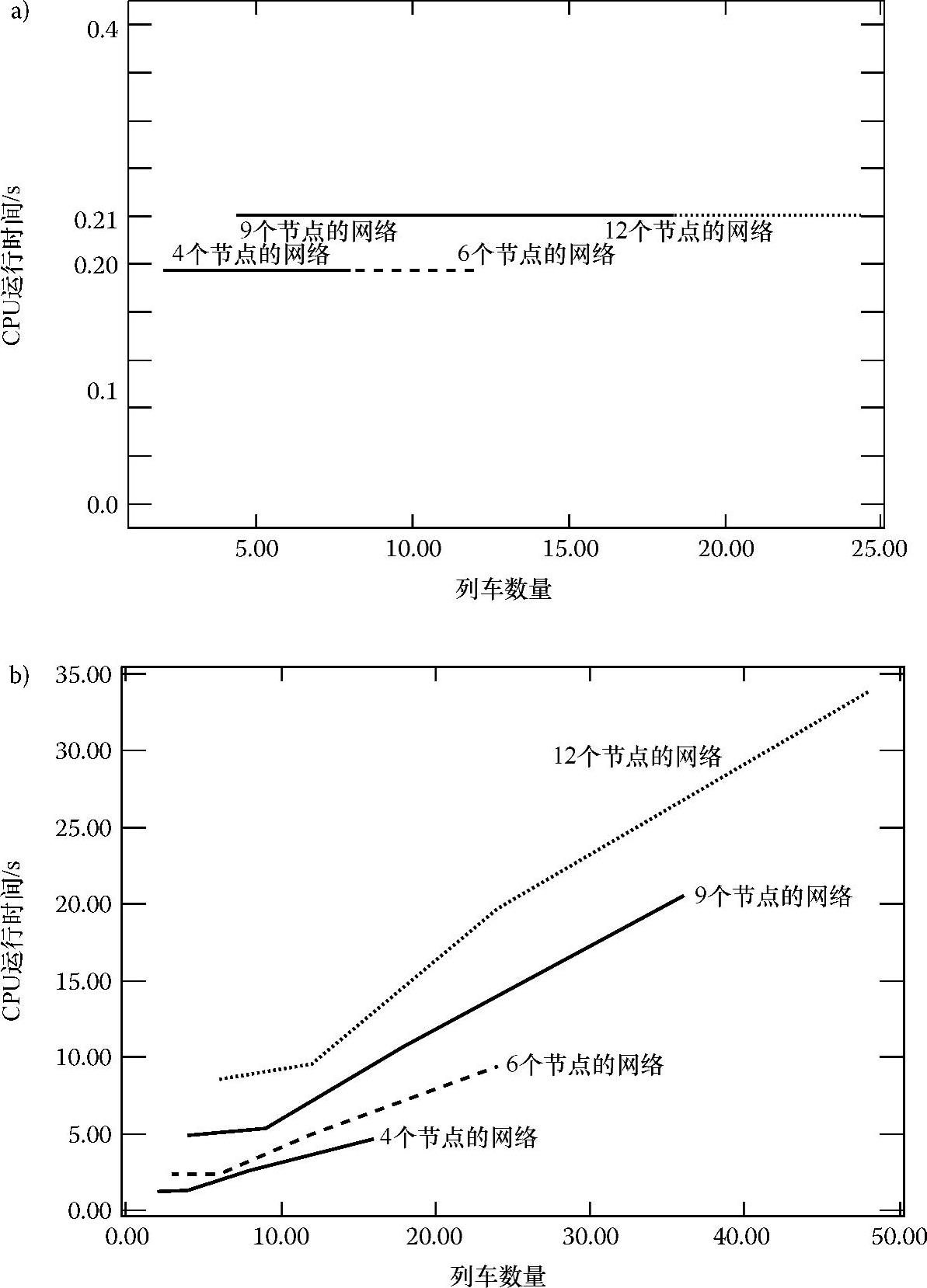
图4.13 4个网络中一列火车的CPU的运行时间与网络中列车数量间的函数关系图

a）DARYN算法 b）传统方法

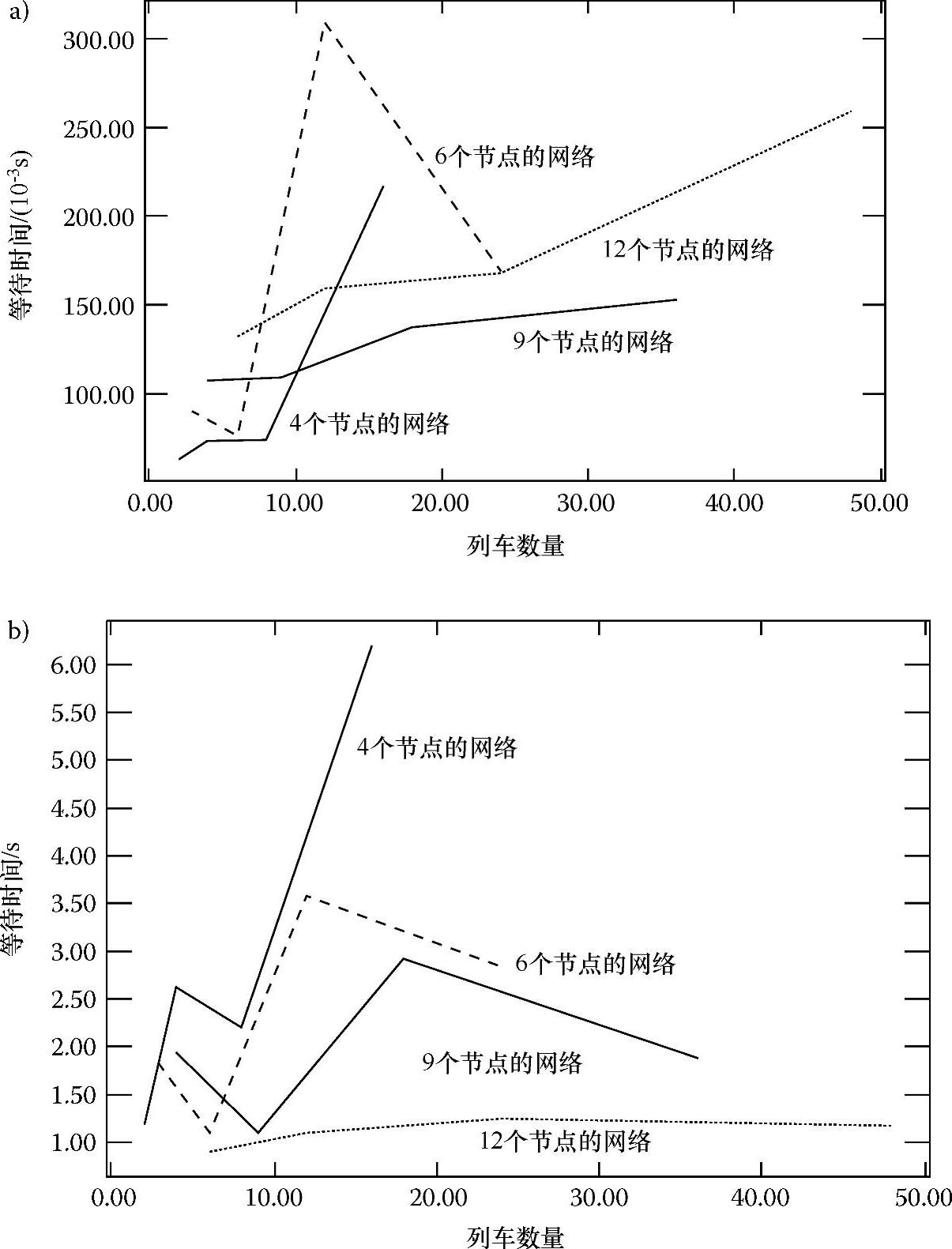
图4.14 4个铁路网中专列的累计空闲时间与列车数量的函数关系图

a）DARYN算法 b）传统方法