实验结果分析及优化进化算法

本节将从收敛性指标、支配性指标和间距指标三个方面分析算法性能。

对表7-1中所给出的每一个测试函数，每种算法独立运行30次，收敛性指标M_c的平均值与标准方差的统计结果见表7-3。同时，为直观查看所得数据是否具有异常值、观察所得数据的偏态与尾重，将所得M_c数据制作成图7-3所示的盒图（box-plot）。图中盒子的上下两条线分别表示样本的上下四分位数，盒子中间的水平线为样本的中位数，盒子上下的虚线表示样本的其余部分（野值除外），样本最大值为虚线顶端，样本最小值为虚线底端，“+”表示野值，盒子的切口为样本的置信区间。

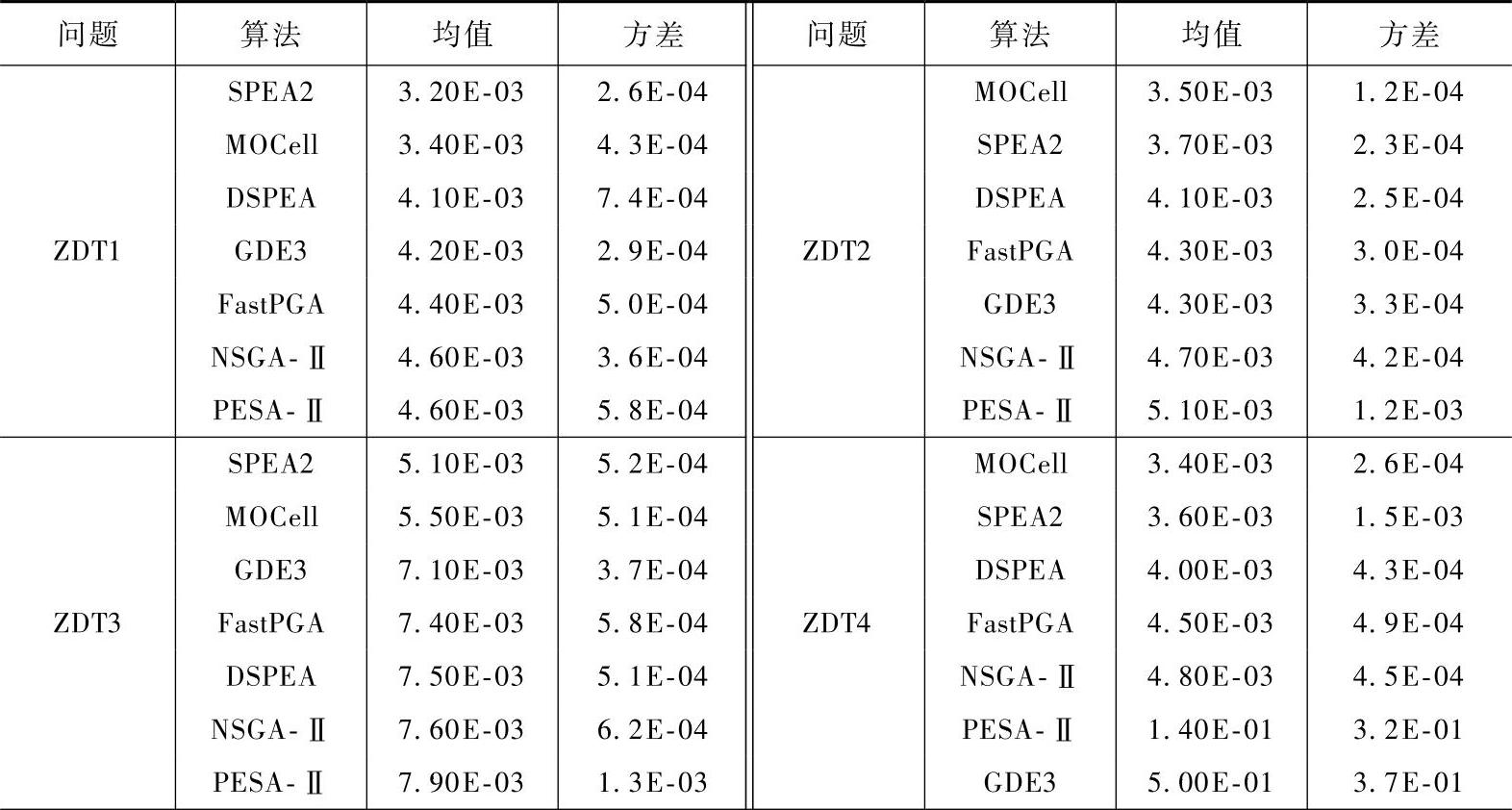
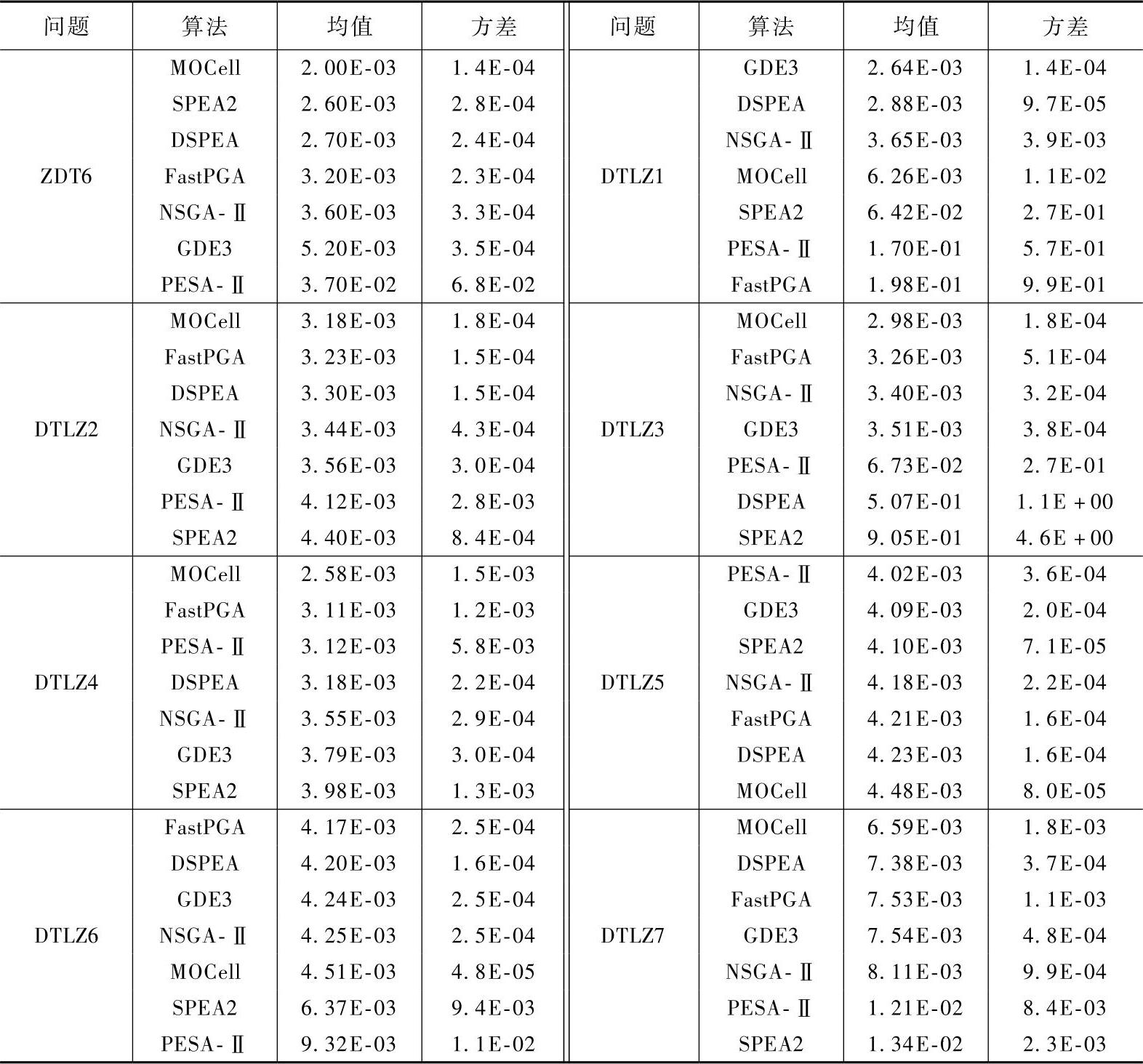
表7-3 FastPGA、GDE3、DSPEA、MOCell、NSGA-Ⅱ、PESA-Ⅱ、SPEA2针对12个测试问题的收敛性指标M_c的平均值与标准方差

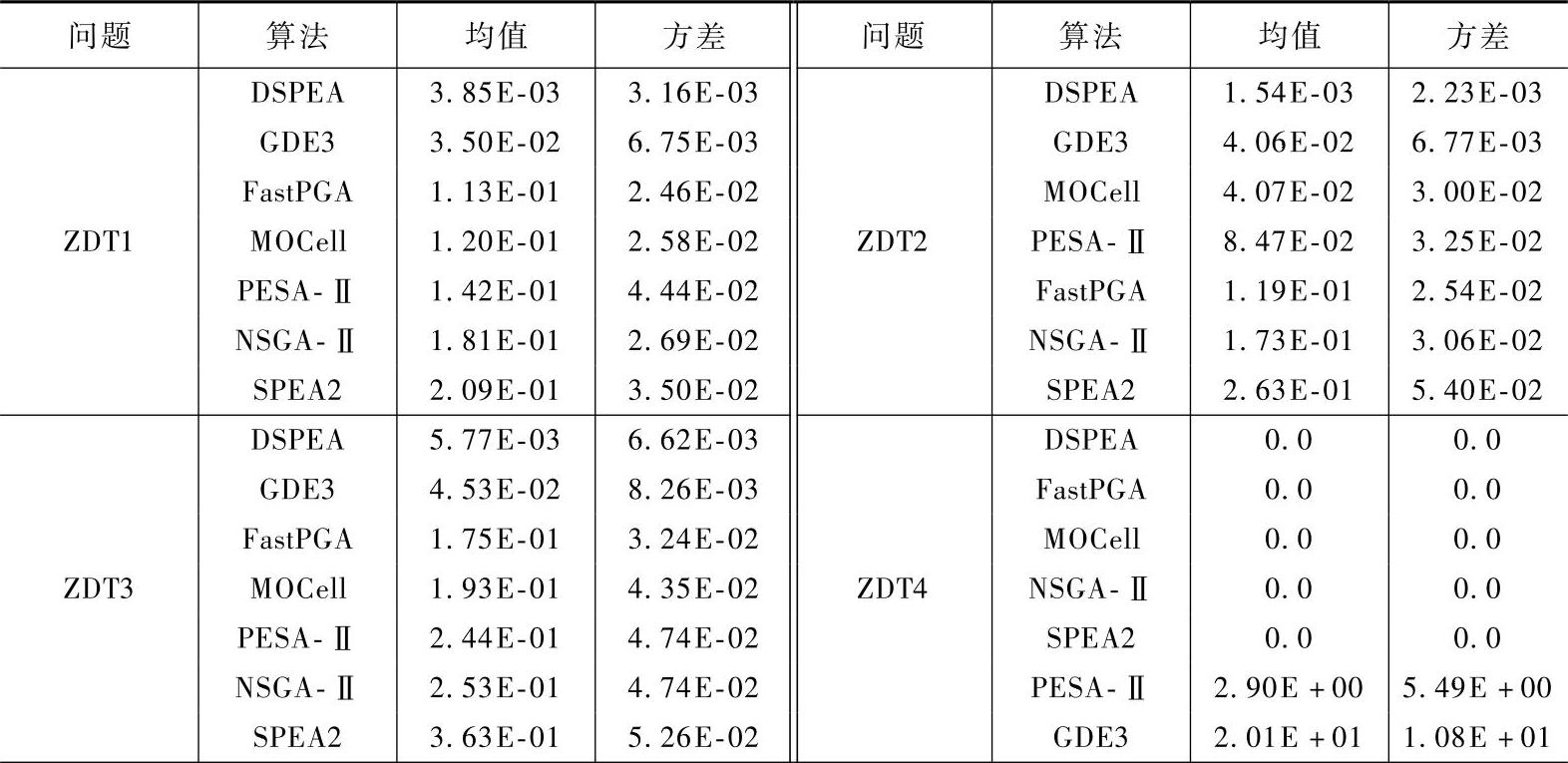
（续）

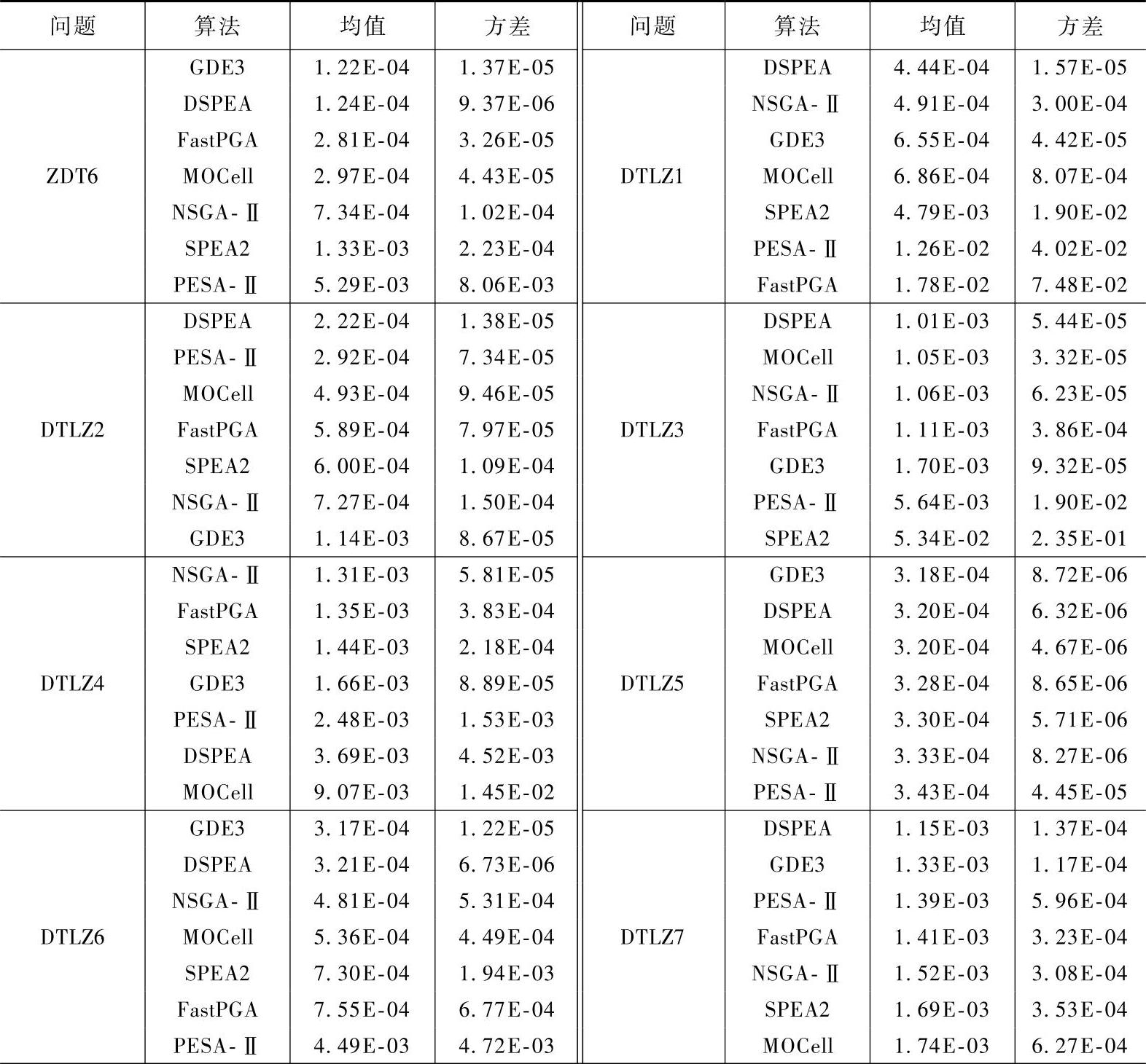
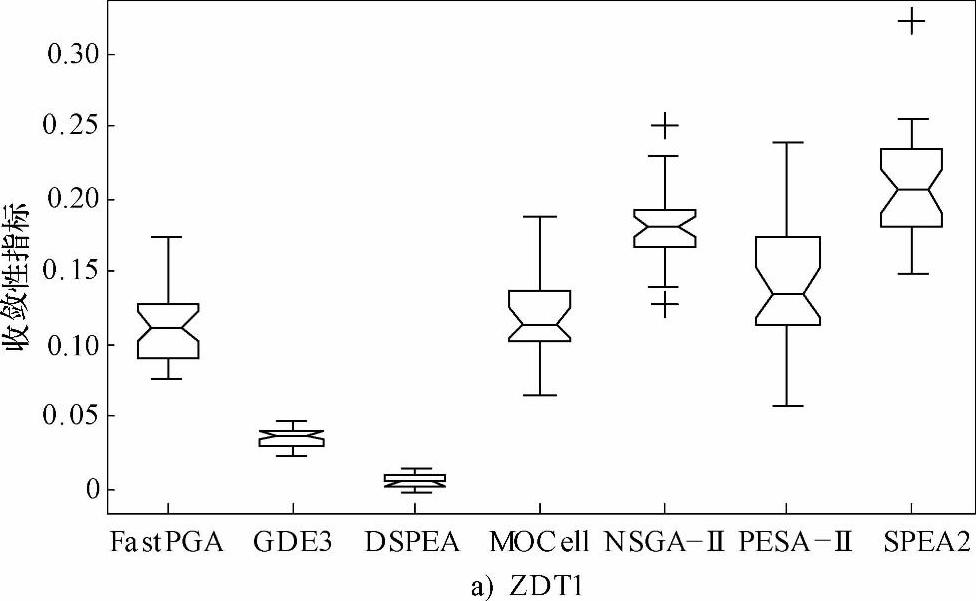
图7-3 FastPGA、GDE3、DSPEA、MOCell、NSGA-Ⅱ、PESA-Ⅱ、SPEA2求解12个测试问题所得收敛性指标的统计盒图

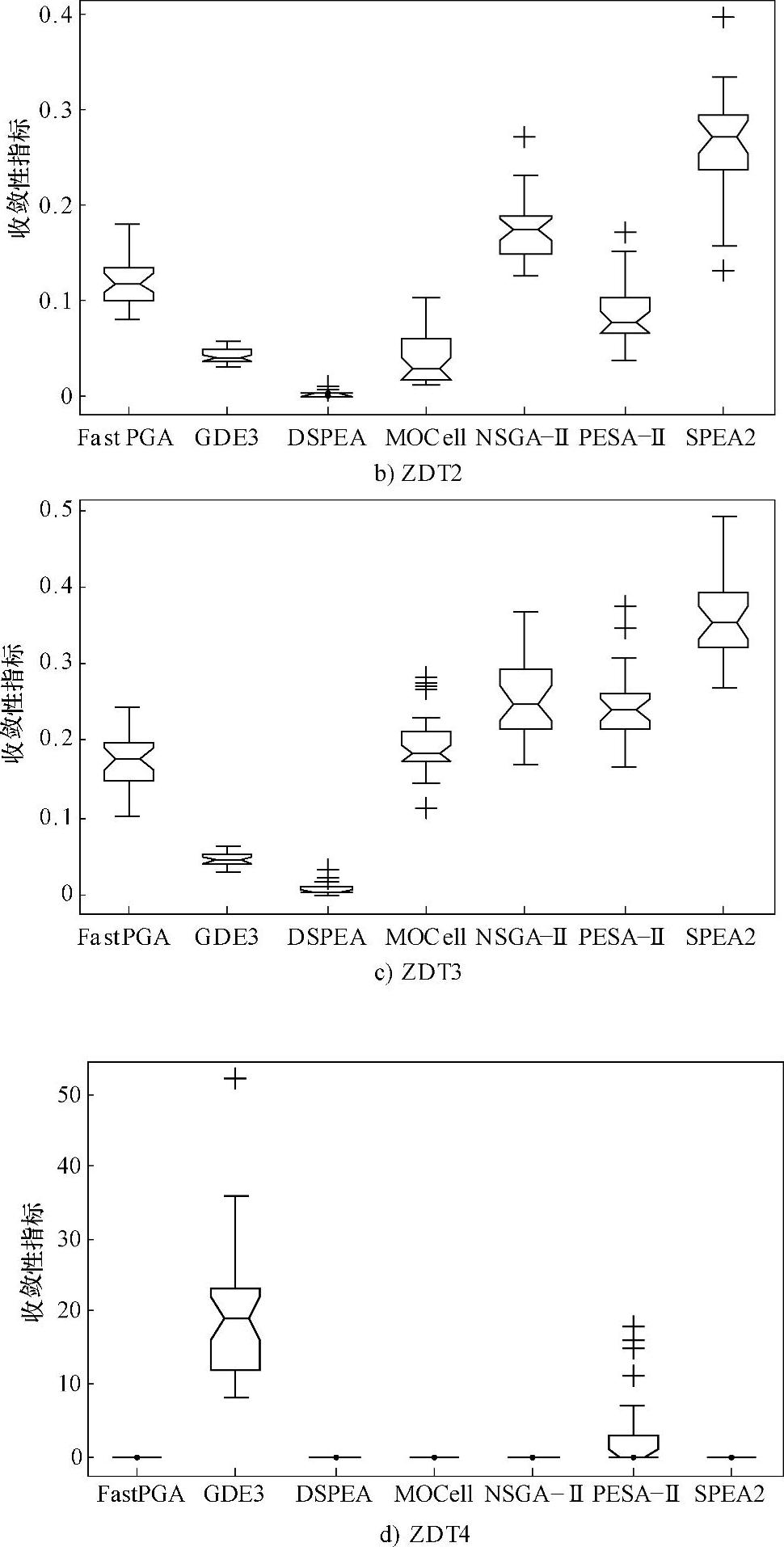
图7-3 FastPGA、GDE3、DSPEA、MOCell、NSGA-Ⅱ、PESA-Ⅱ、SPEA2求解12个测试问题所得收敛性指标的统计盒图（续）

图7-3 FastPGA、GDE3、DSPEA、MOCell、NSGA-Ⅱ、PESA-Ⅱ、SPEA2求解12个测试问题所得收敛性指标的统计盒图（续）

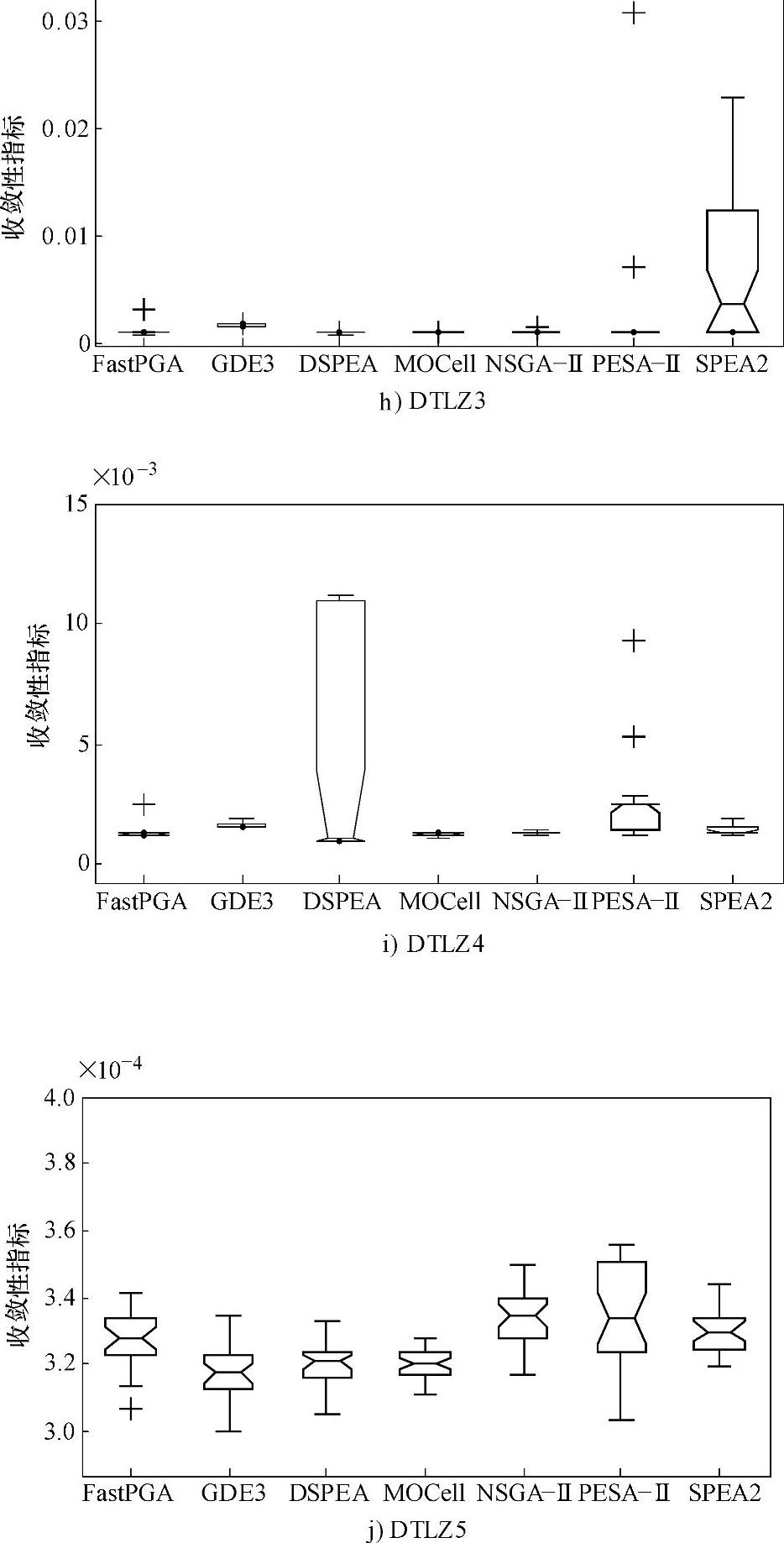
图7-3 FastPGA、GDE3、DSPEA、MOCell、NSGA-Ⅱ、PESA-Ⅱ、SPEA2求解12个测试问题所得收敛性指标的统计盒图（续）

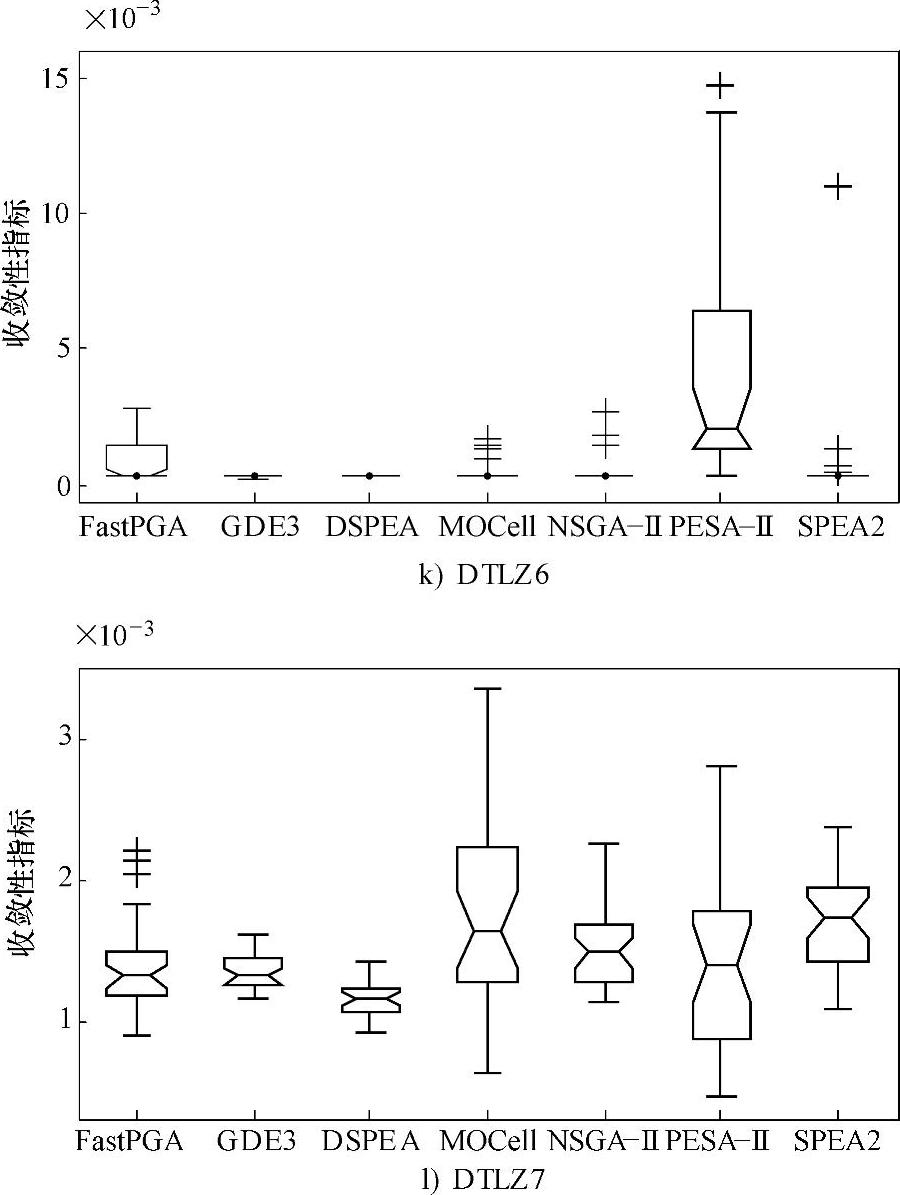
图7-3 FastPGA、GDE3、DSPEA、MOCell、NSGA-Ⅱ、PESA-Ⅱ、SPEA2求解12个测试问题所得收敛性指标的统计盒图（续）

观察图7-3并结合表7-3可知：

1）对于ZDT1，DSPEA的M_c平均值仅为GDE3的11.01%、FastPGA的3.42%、MOCell的3.22%、PESA-Ⅱ的2.72%、NSGA-Ⅱ的2.13%、SPEA2的1.8%；30次所得M_c值制成的盒图中，DSPEA处于最低处且具有小的面积与最对称的盒子切口。

2）对于ZDT4问题，除PESA-Ⅱ与GDE3外，DSPEA及其余算法30次所得解均是真实Pareto前沿的一部分，获得了真正的最优解。(www.xing528.com)

3）对于ZDT6问题，本指标最小的为GDE3的1.2372×10^-4，DSPEA仅以1.18×10^-6之差排第二位，但DSPEA的方差仅为GDE3的68.39%、FastPGA的28.75%、MOCell的21.14%、PESA-Ⅱ的9.18%、NSGA-Ⅱ的4.20%、SPEA2的0.12%；观察盒图可知，DSPEA盒图面积最小且出现的野值处于置信区间的下方，PESA-Ⅱ的盒图面积最大且具有多个偏离较大的野值。

4）对于比较复杂的DTLZ系列，DSPEA在求解DTLZ1、DTLZ2、DTLZ3、DTLZ7时的表现明显优于所采用的对比算法；在求解DTLZ5和DTLZ6时分别以2.03×10^-6与4.5×10^-6之差排在GDE3之后而居第二位。

5）对于DTLZ4问题，所有算法的平均值较其他DTLZ问题的平均值要大一个数量级，而DSPEA的值排在第六位。造成这种结果的原因是所采用的真实Pareto前沿数据集取样偏小且分布比较离散。大多数情况下，进化过程中算法所存储的最优解数量比问题的真实Pareto前沿上的数量小很多。观察图7-4所示出的真实Pareto前沿与算法所得Pareto最优解分布关系可以发现：对于参考数据集P与算法所得的数据集A、B、C、D，虽然数据集A是真实Pareto前沿的一部分，但M_c（A）小于M_c（B）、M_c（C）和M_c（D）。因此，当所参考的Pareto前沿数据集在目标空间上的分布比较稀疏而算法所得解分布相对比较密集时，收敛性指标不能很好地体现解的真实收敛情况。因此，参考数据真实Pareto前沿数据集对收敛性指标具有重要影响。

综上所述，对比算法在不同问题上表现各有所长，但DSPEA在大多数情况下表现更好。特别地，对于大多数测试问题，DSPEA的性能都比NSGA-Ⅱ优良，从这个角度看，提出的决策空间划分模型确实对提高算法性能有积极作用。DSPEA求解ZDT这5个问题时，收敛性指标有4次排第一位，1次以微弱的差距排第二位；在求解DTLZ问题时，收敛性指标有4次排第一位，2次以微弱差距排第二位。对这些测试函数而言，在逼近真实Pareto最优前沿的性能上，DSPEA的表现比FastPGA、GDE3、MOCell、NSGA-Ⅱ、PESA-Ⅱ、SPEA2更好，具有良好的鲁棒性。

独立运行DSPEA、FastPGA、GDE3、MOCell、NSGA-Ⅱ、PESA-Ⅱ、SPEA2求解12个测试问题30次，根据支配性指标的计算方法，DSPEA与对比算法间的最优解支配关系统计结果见表7-4。表中M_d（DSPEA，*）表示DSPEA覆盖对比算法的情况，M_d（*，DSPEA）表示对比算法覆盖DSPEA的情况。观察表7-4可知：对于所有的测试问题，DSPEA都有M_d（DSPEA，*）＞0.5，DSPEA所获得的解优于对比算法的解。很明显，对这些测试函数而言，在获取更高精度的解的性能上，相比FastPGA、GDE3、MOCell、NSGA-Ⅱ、PESA-Ⅱ、SPEA2很有竞争力。

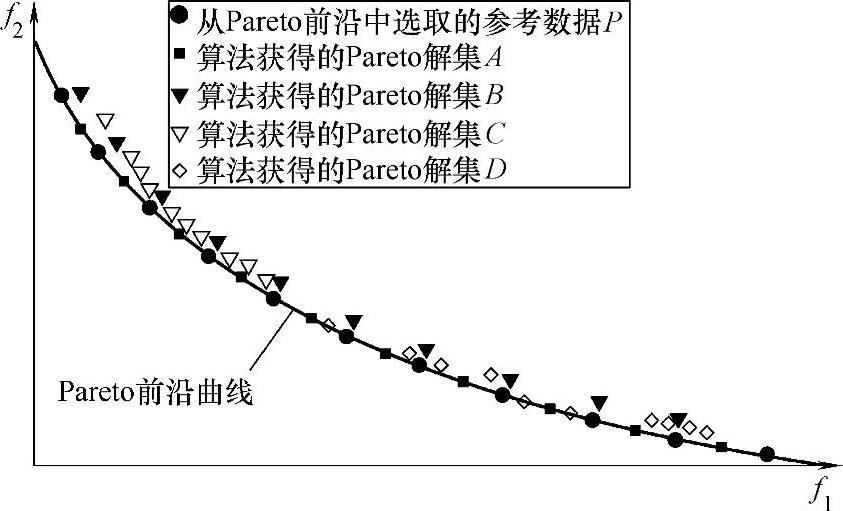
图7-4 Pareto前沿与Pareto最优解可能的分布关系

表7-4 DSPEA与FastPGA、GDE3、MOCell、NSGA-Ⅱ、PESA-Ⅱ、 SPEA2解之间的支配关系统计结果

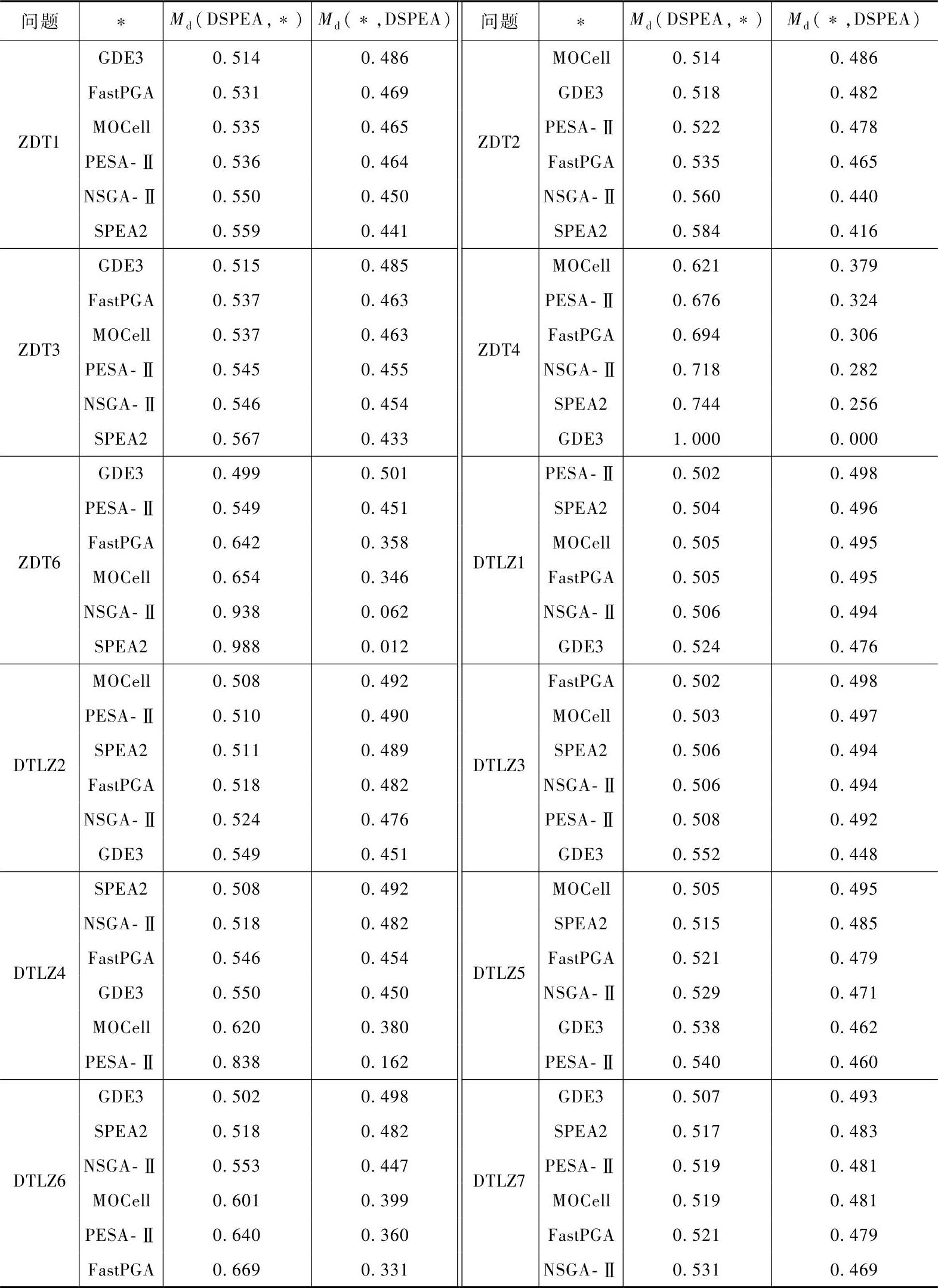
前文分析已指出：对于ZDT4问题，除PESA-Ⅱ与GDE3外，DSPEA及其余算法30次所得解均是真实Pareto前沿的一部分，获得了真正的最优解，但各算法针对ZDT4统计的M_d（DSPEA，*）与M_d（*，DSPEA）的值均不为0.5，而且M_d（DSPEA，*）＞M_d（*，DSPEA），这表明在此问题上，DSPEA所获得解的数量要大于其他算法的数量，DSPEA能够提供数量更多的Pareto最优解。文献[22]指出：SPEA2基于近邻规则的环境选择策略处理精英种群中超出设置规模数量的情况，其得出的解分布的均匀性是很多其他方法无法超越的。本文实验所得的支配关系数据显示，对于本文所测试的ZDT与DTLZ问题，均有M_d（DSPEA，SPEA2）＞0.5＞M_d（SPEA2，DSPEA），不仅表明DSPEA获得的解优于SPEA2所获得的解，还表明DSPEA的解分布广度比SPEA2好。因为按照支配性指标的定义，U是需要计算支配性关系的两个数据集的并集，U内元素互不被支配，只有DSPEA具有好的精度与分布广度才会有M_d（DSPEA，SPEA2）＞0.5＞M_d（SPEA2，DSPEA）成立。这间接表明DSPEA在保证解的分布广度方面具有优势。

表7-5是各算法30次独立运行得出的间距指标M_s的平均值与标准方差。由表7-5可知，对于所测试的12个问题，虽然DSPEA的间距指标没有排第一位的情况，但有8个问题占据前三位且其值与第一位的值差距在15%以内，有5个问题排在素有良好间距指标美誉的SPEA2之前，没有排最后一名的情况。而对比算法中除没有排过第一名的NSGA-Ⅱ外，均有排在最后一位的记录。这可以间接说明DSPEA虽然不能具有最好的分布均匀性，但却能够比较稳定地保持在一定的水平。

表7-5 FastPGA、GDE3、DSPEA、MOCell、NSGA-Ⅱ、PESA-Ⅱ、 SPEA2针对12个测试问题的间距指标M_s的平均值与标准方差

（续）

观察DSPEA与NSGA-Ⅱ对应的各项指标可以发现，除DTLZ4的收敛性指标外，其余所有问题与指标，DSPEA相比于NSGA-Ⅱ具有更好的性能。而DSPEA算法对于超球体的进化是通过NSGA-Ⅱ完成的，它们的繁殖操作完全相同。换言之，正是决策空间划分模型的引入提高了算法的整体性能，DSPEA在收敛精度、收敛稳定性方面具有竞争力，这从实验的角度印证了前文决策空间划分模型的数学基础中所得出的结论。

综上所述，基于12个测试问题与6种具有代表性的对比算法的实验数据与分析表明：DSPEA在逼近Pareto前沿、维持解的均匀分布与广度方面具有竞争力。严格意义上讲，DSPEA为求解多目标优化问题提供了一种新框架，对于超球体的每1轮次进化，对于特定的多目标优化问题，可以根据优化的需求选用任何基于种群操作的算法，DSPEA具有良好的拓展性。