进化算法性能分析：收敛性、支配性和解分布均匀性指标

选用当前被普遍采用的收敛性指标、支配性指标和体现解分布均匀性的间距指标衡量本算法的性能^[4]。

1.收敛性指标Mc

假定A={（a₁，a₂，…，a_A）a_i∈P*}是某一算法得到的Pareto最优解集，即；P={（p₁，p₂，…，p_|P|）p_i∈P^true}是真实Pareto前沿上均匀分布的Pa-reto最优解集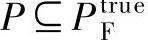，。对于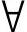a_i∈A距离P的最小归一化欧式距离d_i为

式中，f_k^min与f_k^maX分别是P中第k个目标函数的最小值与最大值。集合A中所有元素d_i的平均值即收敛性指标值M_c（A），其定义为

收敛性指标评价某一算法所获得的Pareto最优解集与真实Pareto前沿的距离。倘若集合P足够完备，即P=P^true，而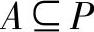，那么M_c（A）=0。一般而言，收敛性指标值越小，则表明算法所得的解越接近真实Pareto前沿。

2.支配性指标Md(www.xing528.com)

设A、B是两组Pareto最优解集合，记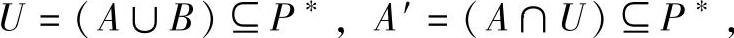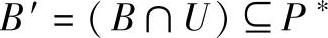，则

由于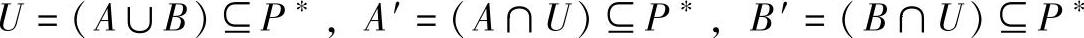，所以A´与B´中的元素均为互不被支配的Pareto最优解。支配性指标体现的是两组解之间的支配关系（或称覆盖关系）。如果M_d（A，B）=1，则表明A集合中的解完全支配（优于/覆盖）B集合中的解，此时可得出M_d（B，A）=0。因此，对于A、B两组Pare-to最优解集，若0≤M_d（B，A）＜M_d（A，B）≤1，则A组解优于B组解。本指标主要用于判定两组解间的优劣关系。

3.间距指标M_s

令A是算法所得的近似Pareto最优解集，即A⊆P^*。间距指标M_s可定义为

式中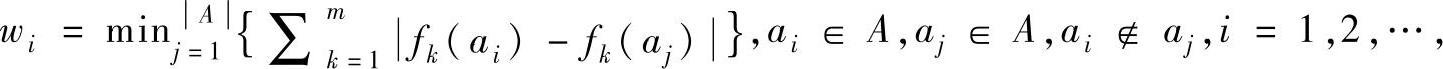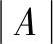，；w是全体w_i的算术平均值；m是前文所定义的目标函数个数。若M_s（A）=0，则表明A的元素在目标空间的分布是等间距的。间距指标M_s（A）的值越小表明集合A中元素在目标空间中的分布越均匀，值越大则离散性越差。