定理证明：决策空间划分模型的数学基础及进化算法

在抽样方法中，分段抽样法^[5]（stratified sampling）将一个多样的总体D划分为l个同质子总体，即首先把样本空间分成子总体D₁，…，D_l，D_i互不相交且∪^l_i=1D_i=D，对每一个子总体进行简单随机抽样，它不仅能全面评估总体的估计，还能获得各段的估计。分段抽样即便是最简单的选取区间和抽样数都能显著减小估计方差，估计精度比简单随机抽样高。分段抽样法涉及两个主要问题^[6]：一是怎样划分抽样区间，常用的方法是将抽样区间等分；二是划分抽样区间后，如何确定抽样次数，通常是按子总体在总体中所占比例确定子总体抽样次数。进化算法的搜索过程，其本质是在决策空间上搜索客观存在的方案以达到预期目标的过程。通过划分决策空间建立多个决策区间模型是否可以提高基于种群操作的算法的搜索准确性？有研究表明种群中个体分布对获得问题的最优解具有重要影响^[1]，且有学者^[2]在研究局部化模型时采用多个互不相交的超球体模型过滤参数噪声，算法的搜索准确性得到了提高，而针对一组单目标组合优化问题的研究成果表明：分布在方案集中的信息对于促进算法搜索到目标结果具有积极作用^[7-11]。受这些研究成果的启发，为了增大基于种群操作的搜索技术在有限时间内捕捉到决策空间中的特定目标的概率，本章研究决策空间上进行多次独立随机抽样的问题，证明决策空间进行划分后的模型比不划分的模型抽中目标的概率更大。

设实数域上连续且均匀分布的决策空间总体集合X可以划分成z个互不相交的同质子总体X₁，X₂，…，X_z，∪^z_i=1X_i=X且它们的元素个数相等，并假定集合X的元素总数量为σ；目标样本集合0={o₁，o₂，…，o_n}（n为集合0的元素数量）且0⊂X。假定在有放回抽样中，抽取规模为K，σ远大于z与K，z能被K整除且大于1。在决策空间总体X上进行K次取样，抽中目标样本o_i（i=1，2，…，n）的概率记为P_β。在决策空间总体X上进行K次取样，分别在z个子决策空间上独立抽取K/z个样本，抽中目标样本o_i的概率记为P_α。为了讨论这个问题，不妨设

决策空间总体X上进行K次取样存在联合概率分布见式（7-1），在z个子决策空间上独立抽取K/z个样本存在联合概率分布见式（7-2）。P_β与P_α是至少y_i=1时的概率。

定理7-1 当σ＞2、n=1及z=2时，P_α＞P_β成立。

证明：根据命题中已知条件，可得

要证P_α＞P_β恒成立，等价于求证P_α-P_β＞0恒成立。因此，将式（7-4）减去式（7-3）整理可得

令b=σ-1，而σ＞2，因此b＞1，将其代入式（7-5）可得

由于K为样本抽取规模，则K≥1。又由b＞1可得b²-1＞0，b²＞b²-1。因此有

联合式（7-6）与式（7-7），可得P_α-P_β＞0成立，命题得证。

定理7-2 当σ＞2、n=1及z＞2时，P_α＞P_β成立。

证明：此定理是定理7-1条件放宽后的情况，在总体上抽中目标样本o_i的概率P_β可由式（7-3）计算。在z个子决策空间上独立抽取K/z个样本，抽中目标样本o_i的概率为

证P_α＞P_β等价于证不等式P_α-P_β＞0恒成立。将式（7-3）与式（7-8）代入不等式左边整理可得

令b=σ-1，联合z＞2代入式（7-9）可得

由于σ＞2，所以b+1＞0。当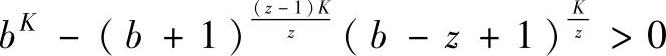成立时，P_α＞P_β恒成立，即证明式（7-11）成立即可。

由于函数lnx在定义域上是单调递增函数，不等式（7-11）左右两边均为正数，因此，不等式（7-11）两边取对数可得等价不等式

令f（z）=Klnb-Kln（b+1）+[Kln（b+1）]/z-[Kln（b-z+1）]/z，整理可得

对式（7-13）的分母进行二项式展开可得式（7-14）与式（7-15）。

将式（7-14）与式（7-15）相减，得

对于式（7-16），当0≤i＜z-1时，Cⁱ_z-zCⁱ_z-1＜0恒成立，而C^z-1_z-zC^z-1_z-1=0，所以存在式（7-17）恒成立。

（b+1）^z-z（b+1）^z-1＜b^z （7-17）

将式（7-17）代入式（7-13），联合已知条件z＞2，可得f（z）＞0恒成立，即P_α-P_β＞0恒成立，命题得证。

定理7-3 当σ＞2、n=2、z=2时，P_α＞P_β恒成立。

证明：在总体上抽中目标样本o_i的概率P_β为

在z个子决策空间上独立抽取K/z个样本，目标样本在空间的分布类型有两种：①两个目标样本存在于同一个子决策空间；②两个目标样本存在于两个不同的决策空间。这两种情况下，抽中目标样本o_i的总概率P_α为

证P_α＞P_β等价于证不等式P_α-P_β＞0恒成立，将式（7-18）与式（7-19）代入不等式左边整理可得式（7-20）。

令b=σ-2，代入式（7-20）化简可得(www.xing528.com)

由已知条件σ＞2得b=σ-2＞0，因此b+2＞0且由于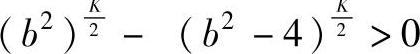成立，即P_α＞P_β恒成立。命题得证。

定理7-4 当σ远大于n且n=2、z＞2时，P_α＞P_β成立。

证明：在总体上抽中目标样本o_i的概率P_β按式（7-18）计算。

在z个子决策空间上独立抽取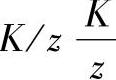个样本，n=2，抽中目标样本o_i的概率P_α为

P_α=1-P_α1-P_α2 （7-22）

式中，P_α1是2个目标样本存在于同一个子决策空间的抽不中的概率；P_α2是两个目标样本存在于不同子决策空间的抽不中的概率。P_α1与P_α2具体为

证P_α＞P_β等价于证不等式P_α-P_β＞0恒成立，联合式（7-20）、式（7-18）、

式（7-23）、式（7-24）整理可得

令b=σ-2＞0，代入式（7-25）整理可得

而z＞2，b+2＞0，式（7-26）大于0恒成立则等价于要求a₁+（z-1）a₂＞0成立。而z-1＞1，因此当a₁与a₂分别大于0时，必定存在a₁+（z-1）a₂＞0恒成立。因此，可以考虑求证不等式（7-27）与式（7-28）同时成立。

不等式（7-27）左右两边均为正数，左右两边取对数所得等价形式为

由不等式（7-29）构造函数f₁（z）整理可得

而柯西平均值定理[12]指出，对于实数序列h₁h₂h₃…h_i…h_n（h_i＞0）存在关系式

当且仅当h₁=h₂=h₃=…=h_i=…=h_n时不等式（7-31）等号成立。

对等式（7-30）中指数部分的分母（b+2）^z-1（b-2z+2）应用均值不等式可得

由于（b+2）≠（b-2z+2），所以不等式（7-32）中等号不成立。将式（7-32）代入式（7-30）右边可得f₁（z）＞0，即

得证不等式（7-27）成立，即式（7-26）中的a₁＞0。

不等式（7-28）左右两边均为正数，左右两边取对数所得等价形式为

由不等式（7-34）构造函数f₂（z）整理可得

同理，根据均值不等式性质^[13]有（b+2）^z-2（b-z+2）≤b^z，同时（b+2）≠（b-z+2），因此f₂（z）＞0成立，得证不等式（7-28）成立，即式（7-26）中的a₂＞0。

联合所得结论a₁＞0与a₂＞0代入式（7-26）可得P_α-P_β＞0恒成立，命题得证。

综合考虑上述4个定理，将它们进行推广，给出以下猜想：

猜想7-1 若实数域上连续且均匀分布的决策空间总体集合X可以划分成z个互不相交的同质子总体X₁，X₂，…，X_z，∪^z_i=1X_i=X且它们的元素个数相等，并假定集合X的元素总数量为σ；目标样本集合0={o₁，o₂，…，o_n}且0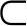X。在决策空间总体X上进行K次取样，抽中目标样本0中元素的概率为P_β。在决策空间总体X上进行K次取样，分别在z个子决策空间上独立抽取K/z个样本，抽中目标样本中元素的概率记为P_α，那么当σ远大于n且n＞2、z＞2时，P_α-P_β＞0恒成立。

综上，对于猜想的证明有待深入研究。4个定理的证明已表明，满足一定条件时划分模型有利于抽中目标。由定理7-2与定理7-4的证明可以得出结论：当目标数量为1或2时，本研究所提出的划分模型抽中目标的概率恒大于不划分模型的概率。若所给出的猜想能够证明，则说明这种划分模型对于目标数量大于2的问题同样有效，模型具有普遍意义。