基于NSGA-Ⅱ的优化算法在混合动力系统优化中的应用

基于NSGA-Ⅱ的带约束并联混合动力系统优化算法（图5-2为流程图）计算步骤为：

1）初始化优化车辆模型、种群规模N、交叉概率、变异概率、最大进化代数G_max，并设t=0；

2）随机生成个体x_i（i=1，2，…，N）初始化种群P_t；

3）计算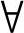x_i∈P_t的目标值f₁（x_i）与f₂（x_i）；

4）对P_t进行非支配排序并计算个体拥挤距离；

5）采用二联赛法从P_t中选取[0.5N]对个体进行交叉、变异操作，产生新种群Q_t；

6）计算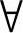x_i∈Q_t的目标值f₁（x_i）与f₂（x_i）；

7）R_t=Q_t∪P_t，同时对R_t进行非支配排序，计算个体的拥挤距离，并根据排序结果从R_t中选择N个个体产生新种群P_t+1，t=t+1；(www.xing528.com)

8）若满足终止条件，则输出P_t+1，否则转到步骤5）。

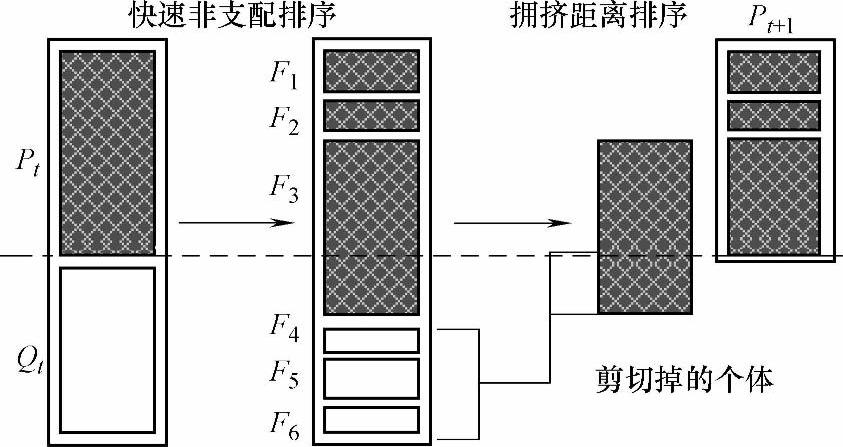
图5-1 NSGA-Ⅱ种群更新示意图

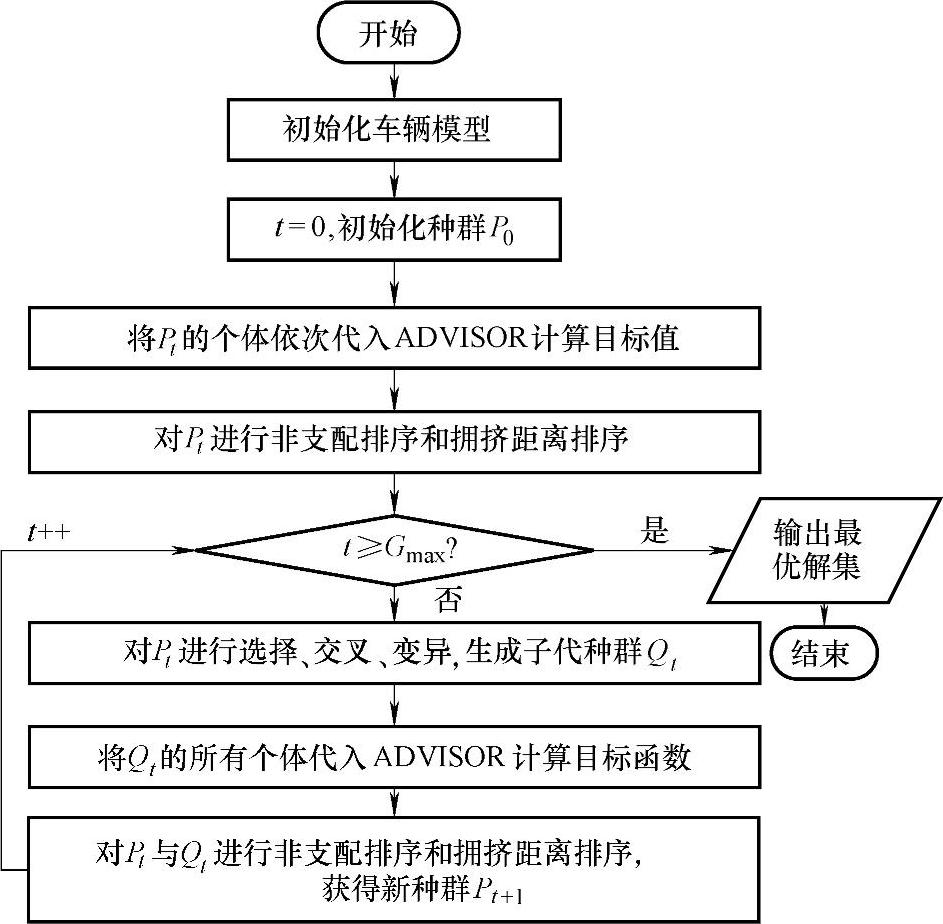
图5-2 cPHS-NSGA算法流程图

算法中，对于候选解x_i采用长度为待优化参数个数的实数表示。在步骤1）中初始化车辆模型时，需要指定具体车型的各待优化参数的取值范围（见表5-2）。步骤3）和6）中，分别对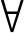x_i∈P_t及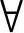x_i∈Q_t调用仿真软件ADVISOR测试给定车型的性能，并根据返回结果计算目标函数f₁（x_i）与f₂（x_i），同时检测x_i是否满足约束条件。如果不满足，将一个足够大的数赋值给f₁（x_i）与f₂（x_i），通过采用这种简单的惩罚方法使得暂时性能不佳的候选解具有较差的适应值，从而减小其繁殖的概率。若不考虑计算候选解适应值部分[即调用仿真软件计算目标值f₁（x_i）与f₂（x_i）部分]外，本算法的计算复杂性与NSGA-Ⅱ相同，它的非支配排序过程最坏情况下的计算复杂性为0（mN²）。